Example 3 - Chapter 10 Class 10 Circles (Important Question)

Transcript

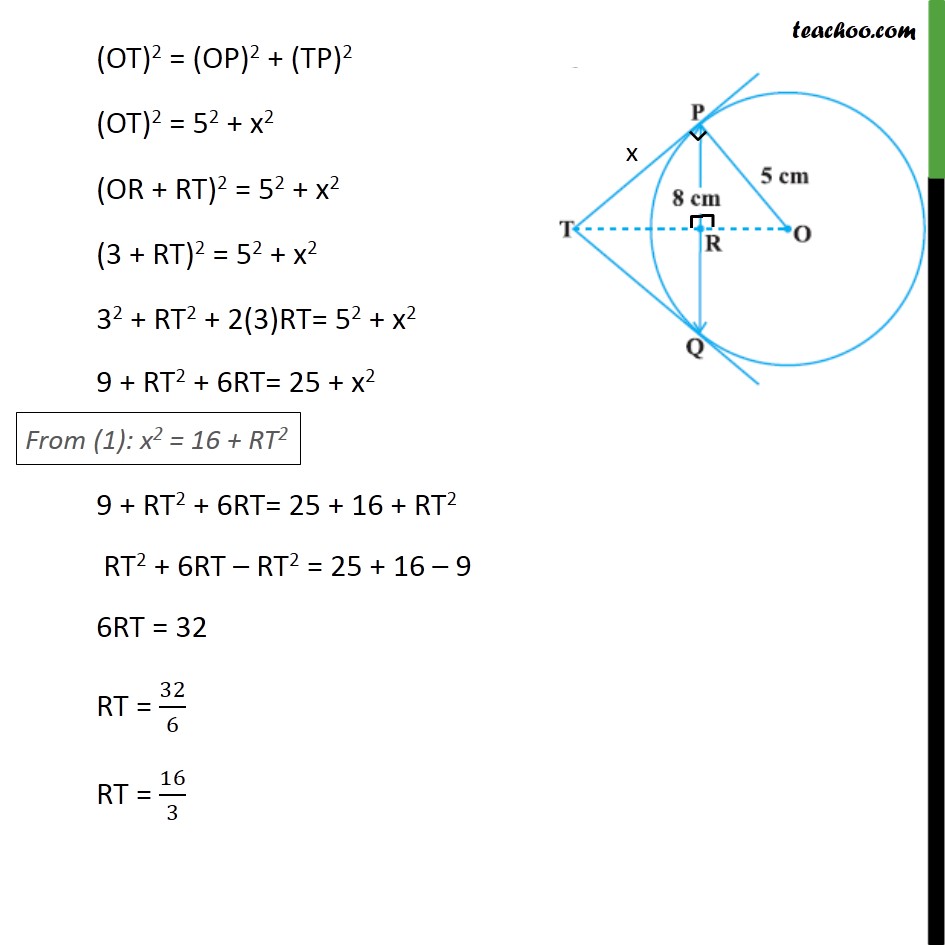
Example 3(Method 1) PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see figure). Find the length TP. Join OT. Let OT intersect PQ at R From theorem 10.2, Lengths of tangents from external point are equal So, TP = TQ In ΔTPQ, TP = TQ, i.e. two sides are equal, So, Δ TPQ is an isosceles triangle Here, OT is bisector of ∠ PTQ, So OT ⊥ PQ Since OT ⊥ PQ So, PR = RQ So, PR = QR = 1/2PQ = 8/2 = 4 cm In right triangle ORP By Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 (OP)2 = (PR)2 + (OR)2 52 = 42 + OR2 25 = 16 + OR2 25 – 16 = OR2 9 = OR2 OR2 = 9 OR = √9 = √(3^2 ) = 3 cm Let TP = x By Pythagoras theorem, (Hypotenuse)2 = (Height)2 + (Base)2 (OT)2 = (OP)2 + (TP)2 (OT)2 = 52 + x2 (OR + RT)2 = 52 + x2 (3 + RT)2 = 52 + x2 32 + RT2 + 2(3)RT= 52 + x2 9 + RT2 + 6RT= 25 + x2 9 + RT2 + 6RT= 25 + 16 + RT2 RT2 + 6RT – RT2 = 25 + 16 – 9 6RT = 32 RT = 32/6 RT = 16/3 From (1) x2 = 16 + RT2 Putting value of RT x2 = 16 + (16/3)^2 x2 = 16 + 256/9 x2 = (16 × 9 + 256)/9 x2 = (144 + 256)/9 x2 = 400/9 x = √(400/9) x = √((20)2/32) = √((20/3)^2 ) = 20/3 Hence, TP = x = 20/3 cm Example 3(Method 2) PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see figure). Find the length TP. Let TP = x Join OQ Since TP is a tangent, OP ⊥ TP ∴ ∠ OPT = 90° Similarly, Since TQ is a tangent, OQ ⊥ TQ ∴ ∠ OQT = 90° In Δ OPT & Δ OQT TP = TQ OT = OT OP = OQ So, Δ OPT ≅ Δ OQT So, ∠ POT = ∠ QOT In Δ OPR & Δ OQR OP = OQ ∠ POR = ∠ QOR OR = OR So, Δ OPR ≅ Δ OQR So, PR = QR So, PR = QR = 1/2PQ = 8/2 = 4 cm Also, Since Δ OPR ≅ Δ OQR So, ∠ PRO = ∠ QRO But, ∠ PRO + ∠ QRO = 180° ∠ PRO + ∠ PRO = 180° 2∠ PRO = 180° ∠ PRO = (180°)/2 ∠ PRO = 90° So, ∠ QRO = 90° Also, ∠ PRT = ∠ QRO = 90° By Pythagoras theorem, (Hypotenuse)2 = (Height)2 + (Base)2 In right triangle ORP By Pythagoras theorem (OP)2 = (PR)2 + (OR)2 52 = 42 + OR2 25 = 16 + OR2 25 – 16 = OR2 9 = OR2 OR2 = 9 OR = √9 OR = √(3^2 ) OR = 3 cm Pythagoras theorem, (Hypotenuse)2 = (Height)2 + (Base)2 9 + RT2 + 6RT= 25 + x2 9 + RT2 + 6RT= 25 + 16 + RT2 RT2 + 6RT – RT2 = 25 + 16 – 9 6RT = 32 RT = 32/6 RT = 16/3 From (3) x2 = 16 + RT2 Putting value of RT x2 = 16 + (16/3)^2 x2 = 16 + 256/9 x2 = (16 × 9 + 256)/9 x2 = (144 + 256)/9 x2 = 400/9 x = √(400/9) x = √((20)2/32) x = √((20/3)^2 ) x = 20/3 Hence, TP = x = 20/3 cm