Check sibling questions

Example 6 - Chapter 10 Class 9 Circles (Term 2)

Last updated at March 16, 2023 by

Example 6 - Prove that quadrilateral formed by internal - Examples

Example 6 - Chapter 10 Class 9 Circles - Part 2
Example 6 - Chapter 10 Class 9 Circles - Part 3

This video is only available for Teachoo black users

Subscribe Now

Get live Maths 1-on-1 Classs - Class 6 to 12

Book 30 minute class for ₹ 499 ₹ 299

Transcript

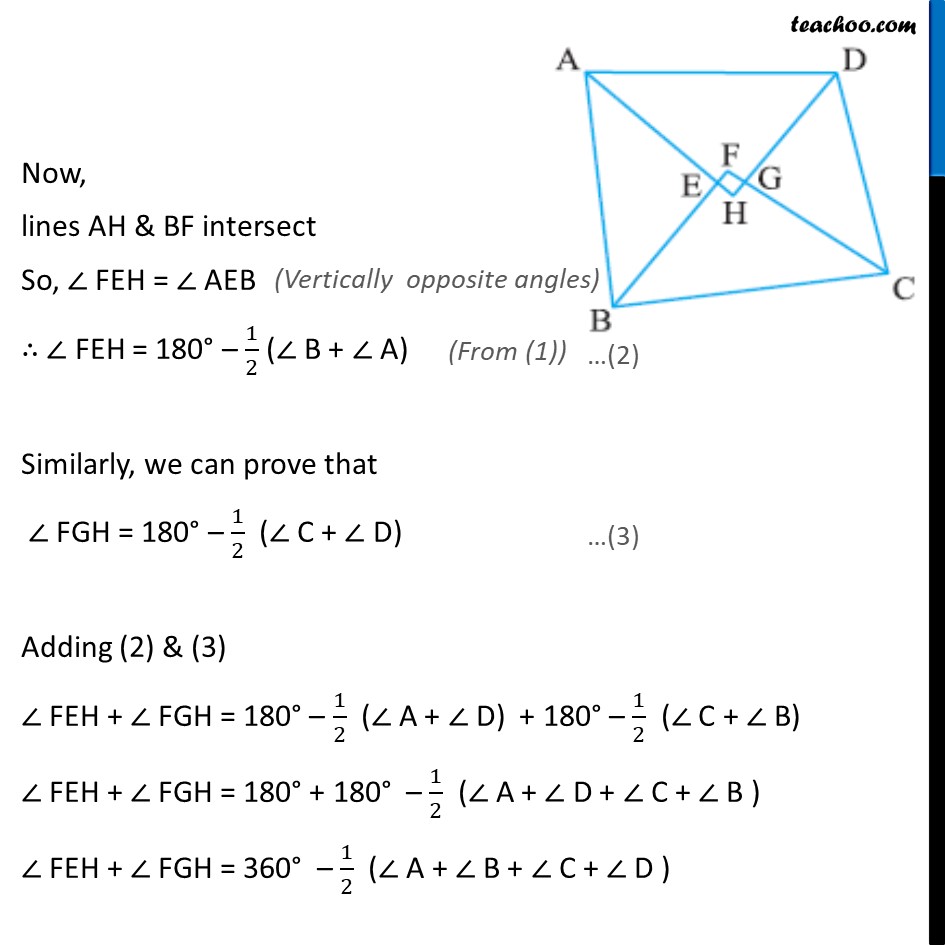
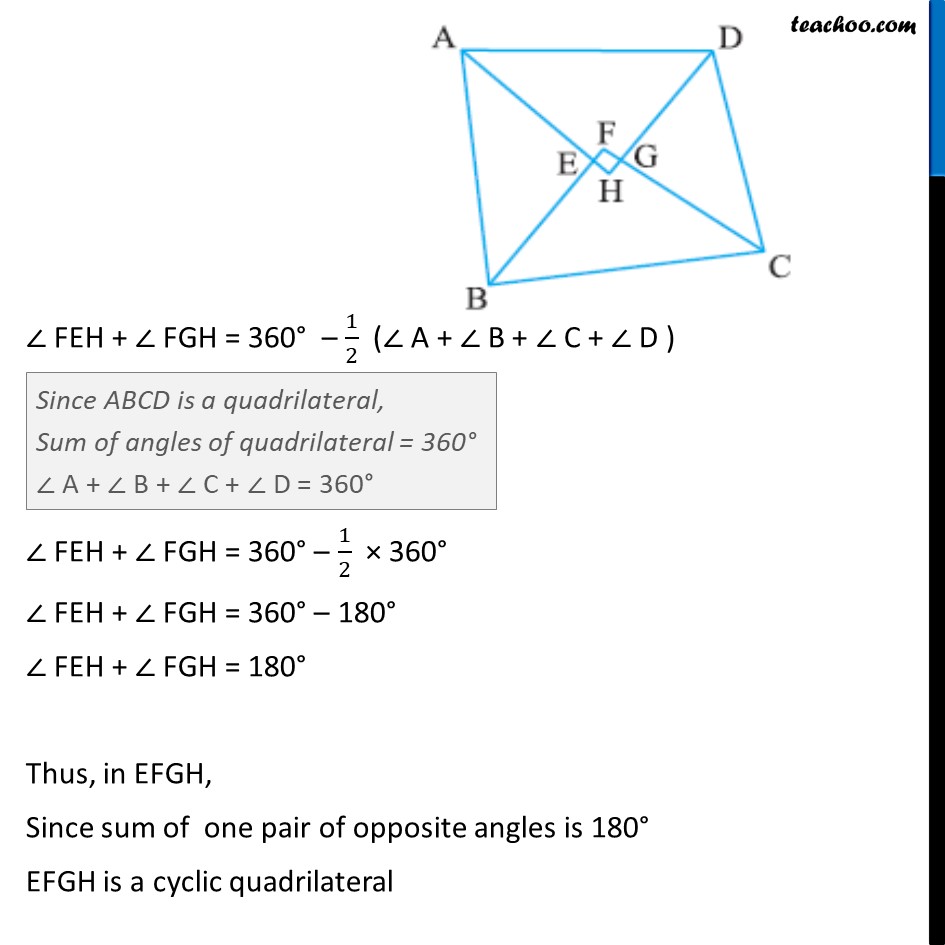
Example 6 Prove that the quadrilateral formed (if possible) by the internal angle bisectors of any quadrilateral is cyclic. Given: ABCD is a quadrilateral AH, BF, CF, DH are bisectors of A , B, C, D respectively To prove: EFGH is cyclic quadrilateral Proof: To prove EFGH is a cyclic quadrilateral, we prove that sum of one pair of opposite angles is 180 In AEB ABE + BAE + AEB = 180 AEB = 180 ABE BAE AEB = 180 (1/2 B + 1/2 A) AEB = 180 1/2 ( B + A) Now, lines AH & BF intersect So, FEH = AEB FEH = 180 1/2 ( B + A) Similarly, we can prove that FGH = 180 1/2 ( C + D) Adding (2) & (3) FEH + FGH = 180 1/2 ( A + D) + 180 1/2 ( C + B) FEH + FGH = 180 + 180 1/2 ( A + D + C + B ) FEH + FGH = 360 1/2 ( A + B + C + D ) FEH + FGH = 360 1/2 ( A + B + C + D ) FEH + FGH = 360 1/2 360 FEH + FGH = 360 180 FEH + FGH = 180 Thus, in EFGH, Since sum of one pair of opposite angles is 180 EFGH is a cyclic quadrilateral

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.