Question 3 - Circle passing through 3 points - Chapter 9 Class 9 Circles

Transcript

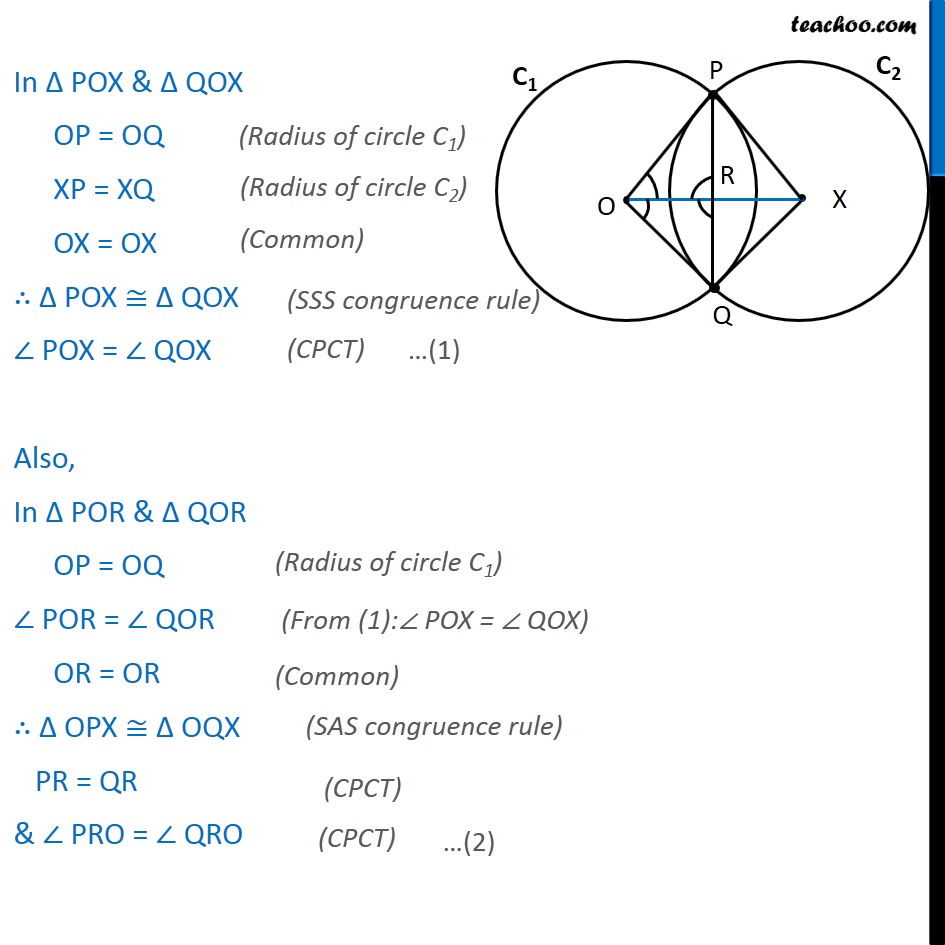
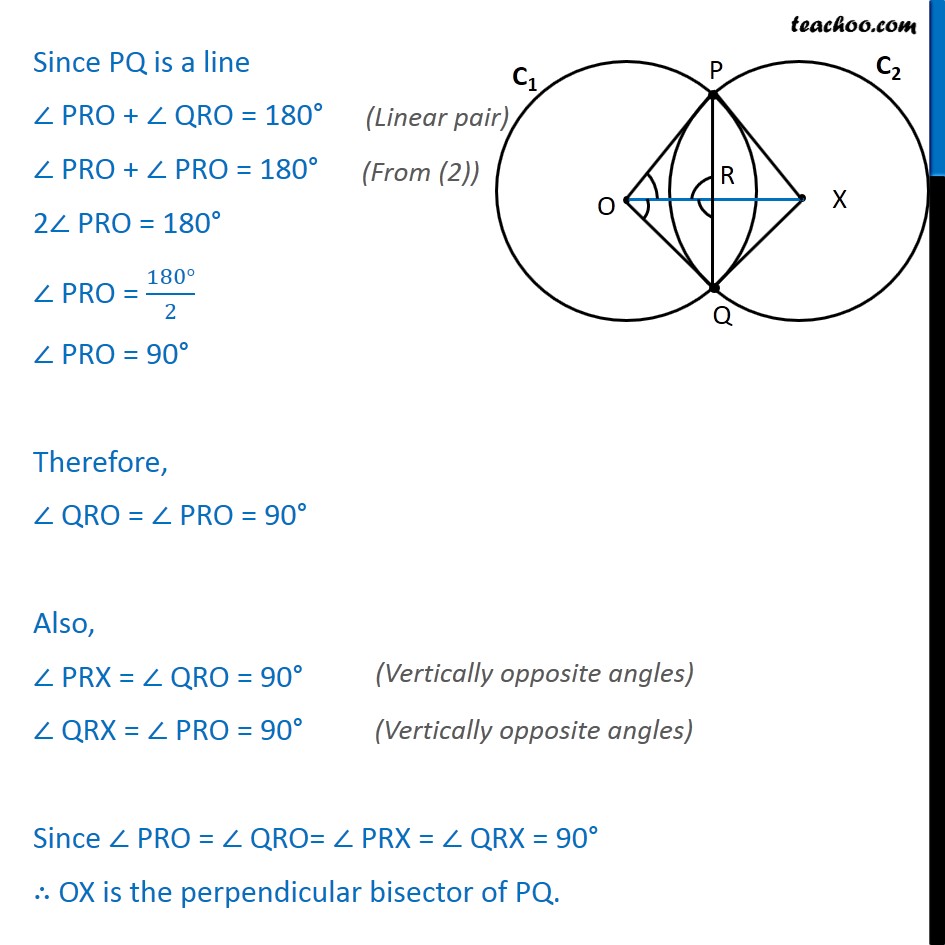
Question 3 If two circles intersect at two points, then prove that their centres lie on the perpendicular bisector of the common chord. Given: Let circle C1 have center O & circle C2 have center X, PQ is the common chord To prove: OX is the perpendicular bisector of PQ i.e. PR = RQ ∠ PRO = ∠ PRX = ∠ QRO = ∠ QRX = 90° Construction: Join PO, PX, QO, QX Proof: In Δ POX & Δ QOX OP = OQ XP = XQ OX = OX ∴ Δ POX ≅ Δ QOX ∠ POX = ∠ QOX Also, In Δ POR & Δ QOR OP = OQ ∠ POR = ∠ QOR OR = OR ∴ Δ OPX ≅ Δ OQX PR = QR & ∠ PRO = ∠ QRO Since PQ is a line ∠ PRO + ∠ QRO = 180° ∠ PRO + ∠ PRO = 180° 2∠ PRO = 180° ∠ PRO = (180°)/2 ∠ PRO = 90° Therefore, ∠ QRO = ∠ PRO = 90° Also, ∠ PRX = ∠ QRO = 90° ∠ QRX = ∠ PRO = 90° Since ∠ PRO = ∠ QRO= ∠ PRX = ∠ QRX = 90° ∴ OX is the perpendicular bisector of PQ.