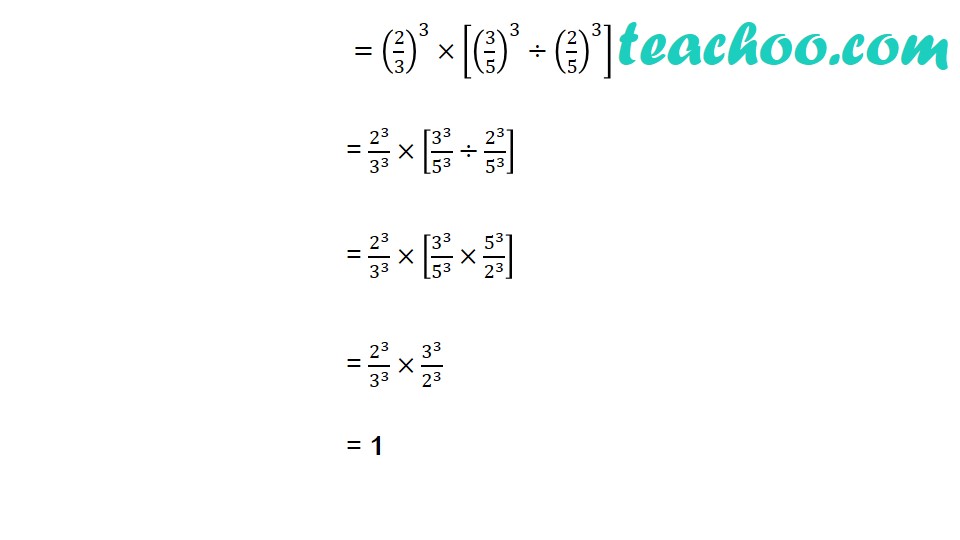
Practice Questions on Laws of Exponents

Last updated at Dec. 16, 2024 by

Check the videos below, or you can...

Download the full summary
Chapter 1 Class 9 Chapter Summary - Part 8 Laws of Exponents.pdf
 
 

Practice Questions on Laws of Exponents - with videos - Teachoo

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 2

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 3

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 4

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 5

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 6

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 7

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 8 Practice Questions on Laws of Exponents - Part 9 Practice Questions on Laws of Exponents - Part 10

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 11

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Practice Questions on Laws of Exponents - Part 12

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

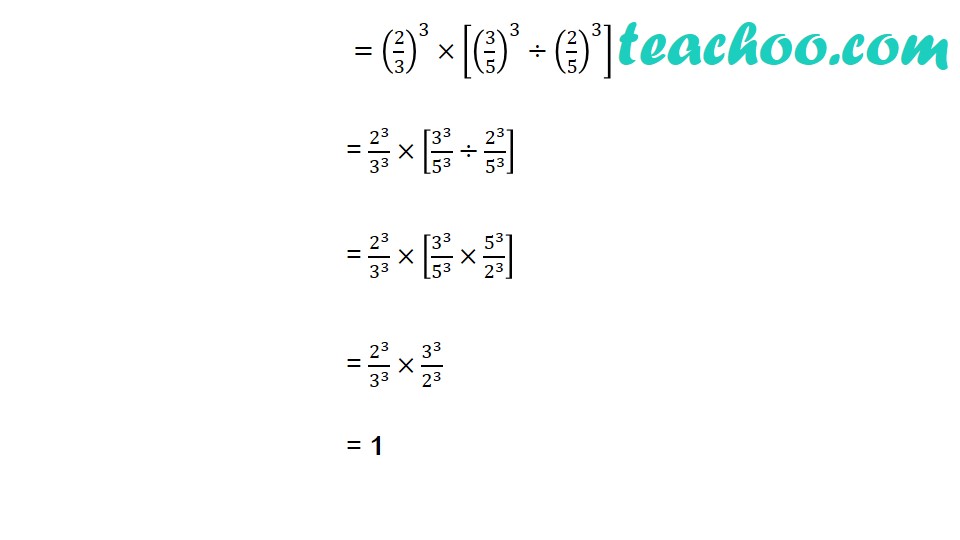
Practice Questions on Laws of Exponents - Part 13 Practice Questions on Laws of Exponents - Part 14   

 

Something went wrong!

The video couldn't load due to a technical hiccup.
But don't worry — our team is already on it, and we're working hard to get it back up ASAP.

Thanks for bearing with us!

Share on WhatsApp

Transcript

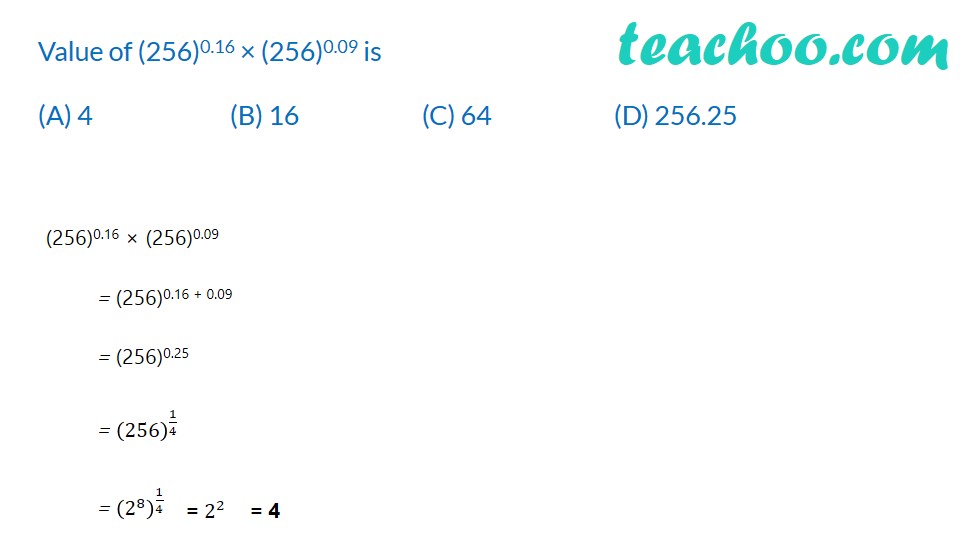
Find (2/3)^2 ×(2/5)^(−3) × (3/5)^2 (2/3)^2 ×(2/5)^(−3) × (3/5)^2 = (2/3)^2 ×(5/2)^3 × (3/5)^2 = 2^2/3^2 × 5^3/2^3 × 3^2/5^2 = 𝟓/𝟐 Evaluate (i) ∛((343)^(−2) ) ∛((343)^(−2) ) = [(343)^(−2) ]^(1/3) = (343)^(−2 × 1/3) = (7^3 )^( (−2)/3) = 7^[3 × ((−2)/3)] = 7^(−2) = 1/7^2 = 1/49 (ii) √(5&(32)^(−3) ) √(5&(32)^(−3) ) = [(32)^(−3) ]^(1/5) = (32)^(−3 × 1/5) = (2^5 )^( (−3)/5) = 2^[5 × ((−3)/5)] = 2^(−3) = 1/2^3 = 1/8 Which of the following is not equal to [(5/6)^(1/5) ]^((−1)/6) (a) 1/[(5/6)^(1/5) ]^(1/6) (b) (6/5)^(1/30) (c) (5/6)^((−1)/30) (d) (5/6)^(1/5 − 1/6) Value of (256)0.16 × (256)0.09 is (A) 4 (B) 16 (C) 64 (D) 256.25 (256)0.16 × (256)0.09 = (256)0.16 + 0.09 = (256)0.25 = (256)^(1/4) = (2^8 )^(1/4) Which of the following is equal to x (a) 𝑥^(12/7)−𝑥^(5/7) (b) √(12&(𝑥^4 )^(1/3) ) (c) (√(𝑥^3 ))^(2/3) (d) 𝑥^(12/7) × 𝑥^(5/7) Find value of x, if 5x−3 × 32x−8 = 225 Given 5x − 3 × 32x − 8 = 225 5x − 3 × 32x − 8 = 25 × 9 5x − 3 × 32x − 8 = 52 × 32 Comparing powers of 5 and 3 If 〖25〗^(𝑥 − 1)=5^(2𝑥 − 1)−100, find the value of x Given 〖25〗^(𝑥 − 1)=5^(2𝑥 − 1)−100 〖(5^2)〗^(𝑥 − 1)=5^(2𝑥 − 1)−100 5^(2𝑥 − 2)=5^(2𝑥 − 1)−100 5^(2𝑥 − 2)− 5^(2𝑥 − 1)=−100 5^2𝑥 × 5^(−2)− 5^2𝑥 × 5^(−1)=−100 5^2𝑥/5^2 −5^2𝑥/5 =−100 5^2𝑥 (1/5^2 −1/5) =−100 5^2𝑥 ((1 − 5)/5^2 ) =−100 5^2𝑥 ((−4)/5^2 ) =−100 5^2𝑥 =100 ×5^2/4 5^2𝑥 =25 × 25 5^2𝑥 =5^2 × 5^2 Prove that (2^30 + 2^29+ 2^28)/(2^31 + 2^30 − 2^29 ) = 7/10 We have (2^30 + 2^29+ 2^28)/(2^31 + 2^30 − 2^29 ) = (2^28 (2^2 + 2 + 1))/(2^29 (2^2 + 2 − 1)) = (2^28 (4 + 2 + 1))/(2^29 (4 + 2 − 1)) = 2^((28 − 29))× 7/5 Simplify: [5 (8^(1/3)+〖27〗^(1/3) )^3 ]^(1/4) [5 (8^(1/3)+〖27〗^(1/3) )^3 ]^(1/4) = [5 (〖(2^3)〗^(1/3)+〖(3^3)〗^(1/3) )^3 ]^(1/4) = [5 (2+3)^3 ]^(1/4) = [5 (5)^3 ]^(1/4) = [5^4 ]^(1/4) Simplify (81/16)^(−3/4)×[(25/9)^((−3)/2)÷(5/2)^(−3) ] (81/16)^(−3/4)×[(25/9)^((−3)/2)÷(5/2)^(−3) ] = [(3/2)^4 ]^(−3/4)×[[(5/3)^2 ]^((−3)/2)÷(5/2)^(−3) ] = (3/2)^(−3)×[(5/3)^(−3)÷(5/2)^(−3) ] =(2/3)^3×[(3/5)^3÷(2/5)^3 ] = 2^3/3^3 ×[3^3/5^3 ÷2^3/5^3 ] = 2^3/3^3 ×[3^3/5^3 ×5^3/2^3 ] = 2^3/3^3 ×3^3/2^3 = 1

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo