Question 6 - Important Questions on Lines, Angles, Triangles - Chapter 6 Class 9 Lines and Angles

Transcript

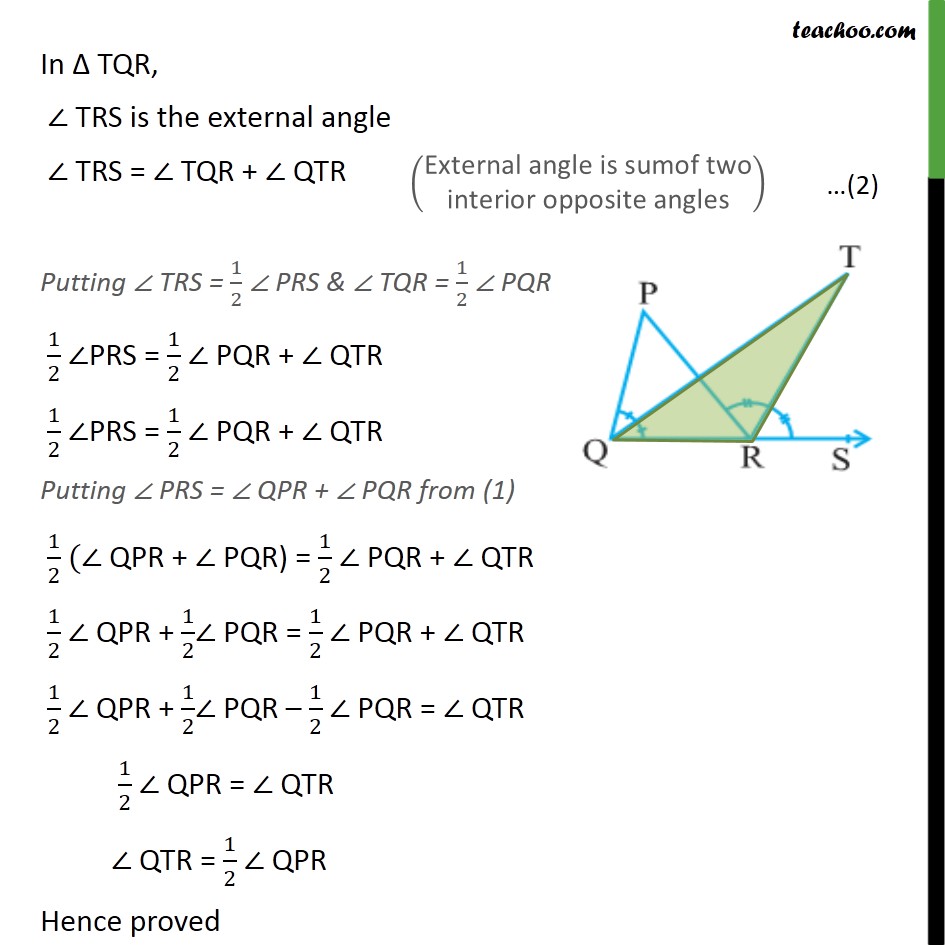
Ex 6.3 ,6 In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR= 1/2 ∠QPR Given TQ is the bisector of ∠ PQR. So, ∠ PQT = ∠ TQR = 1/2 ∠ PQR Also, TR is the bisector of ∠ PRS So, ∠ PRT = ∠ TRS = 1/2 ∠ PRS In Δ PQR, ∠ PRS is the external angle ∠ PRS = ∠ QPR + ∠ PQR In Δ TQR, ∠ TRS is the external angle ∠ TRS = ∠ TQR + ∠ QTR Putting ∠ TRS = 1/2 ∠ PRS & ∠ TQR = 1/2 ∠ PQR 1/2 ∠PRS = 1/2 ∠ PQR + ∠ QTR 1/2 ∠PRS = 1/2 ∠ PQR + ∠ QTR Putting ∠ PRS = ∠ QPR + ∠ PQR from (1) 1/2 (∠ QPR + ∠ PQR) = 1/2 ∠ PQR + ∠ QTR 1/2 ∠ QPR + 1/2∠ PQR = 1/2 ∠ PQR + ∠ QTR 1/2 ∠ QPR + 1/2∠ PQR – 1/2 ∠ PQR = ∠ QTR 1/2 ∠ QPR = ∠ QTR ∠ QTR = 1/2 ∠ QPR Hence proved