Question 2 - Important Questions on Lines, Angles, Triangles - Chapter 6 Class 9 Lines and Angles

Last updated at May 29, 2023 by

Ex 6.3, 2 - In figure, ∠X = 62°, ∠XYZ = 54°. If YO & ZO - Triangle - Problems

Ex 6.3, 2 - Chapter 6 Class 9 Lines and Angles - Part 2

Ex 6.3, 2 - Chapter 6 Class 9 Lines and Angles - Part 3

Learn in your speed, with individual attention - Teachoo Maths 1-on-1 Class

Book a free demo

Transcript

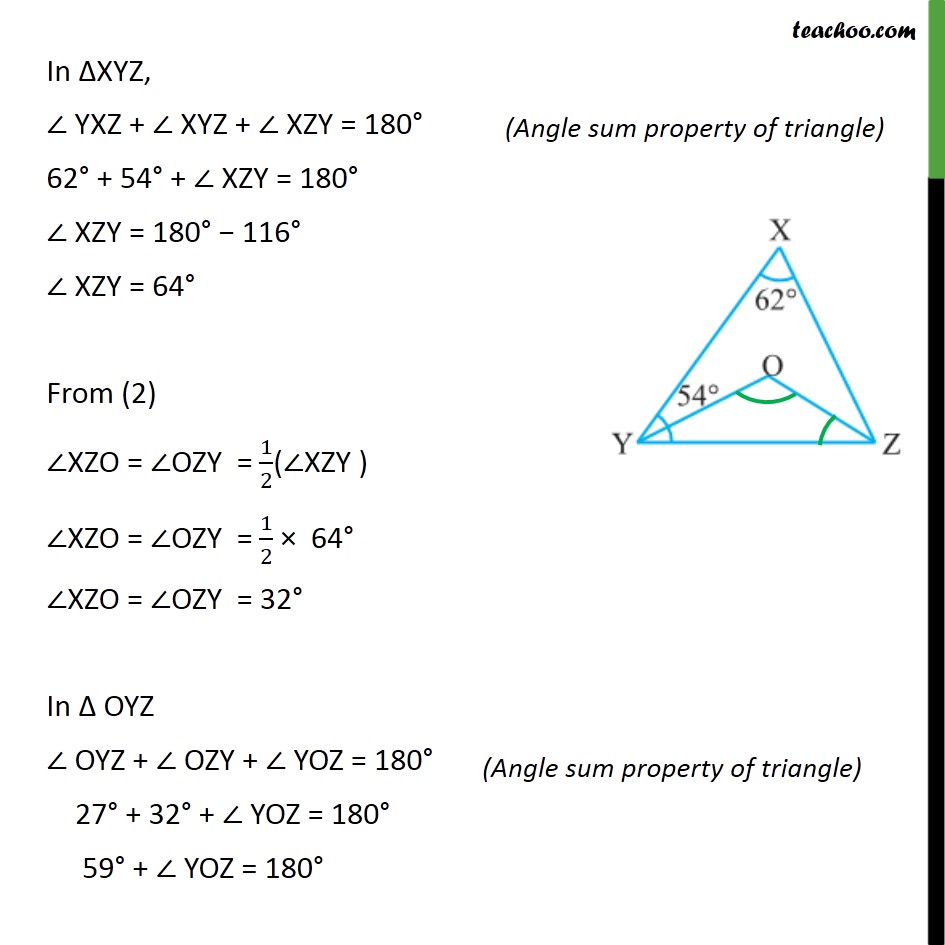
Question 2 In the given figure, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ. Given, OY is the angle bisector of ∠XYZ So, ∠XYO = ∠OYZ = 1/2(∠XYZ ) ∠XYO = ∠OYZ = 1/2 (54°) ∠XYO = ∠OYZ = 27° Also, OZ is the angle bisector of ∠XZY So, ∠XZO = ∠OZY = 1/2(∠XZY ) In ΔXYZ, ∠ YXZ + ∠ XYZ + ∠ XZY = 180° 62° + 54° + ∠ XZY = 180° ∠ XZY = 180° − 116° ∠ XZY = 64° From (2) ∠XZO = ∠OZY = 1/2(∠XZY ) ∠XZO = ∠OZY = 1/2 × 64° ∠XZO = ∠OZY = 32° In Δ OYZ ∠ OYZ + ∠ OZY + ∠ YOZ = 180° 27° + 32° + ∠ YOZ = 180° 59° + ∠ YOZ = 180° 59° + ∠ YOZ = 180° ∠YOZ = 180° − 59° ∠YOZ = 121°

Ask a doubt
Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 13 years. He provides courses for Maths, Science, Social Science, Physics, Chemistry, Computer Science at Teachoo.