







Ex 10.1
Last updated at Dec. 16, 2024 by Teachoo












Transcript
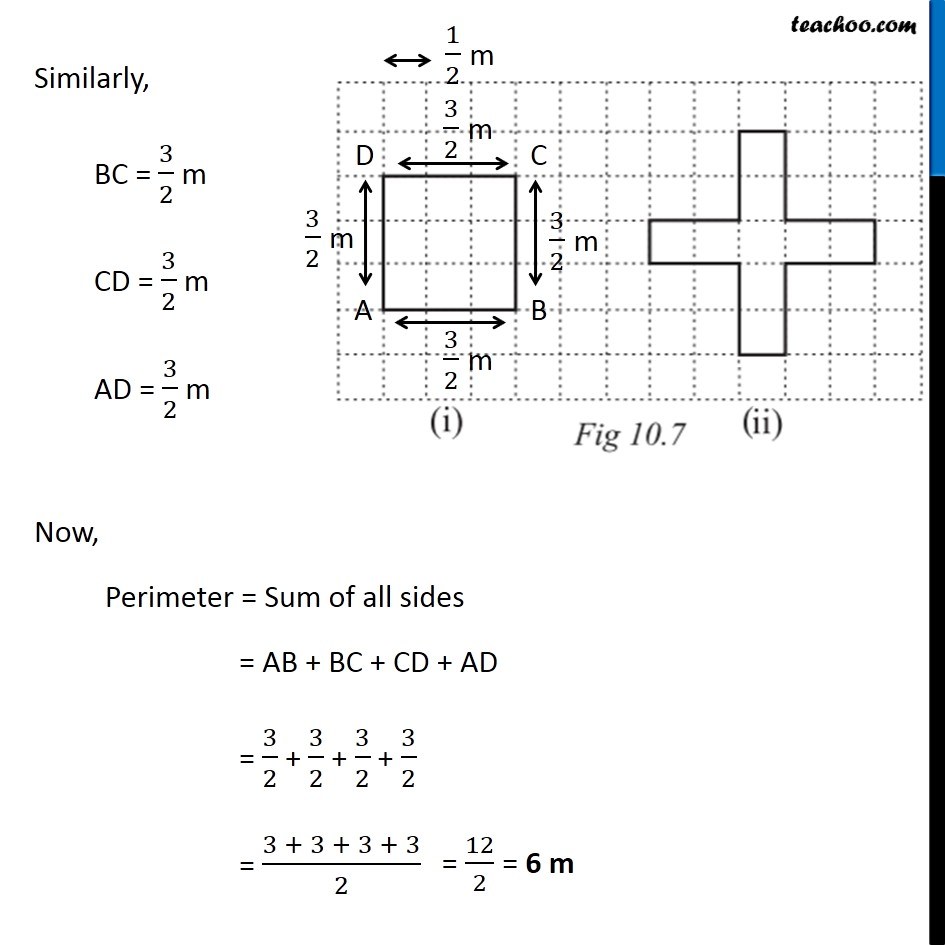
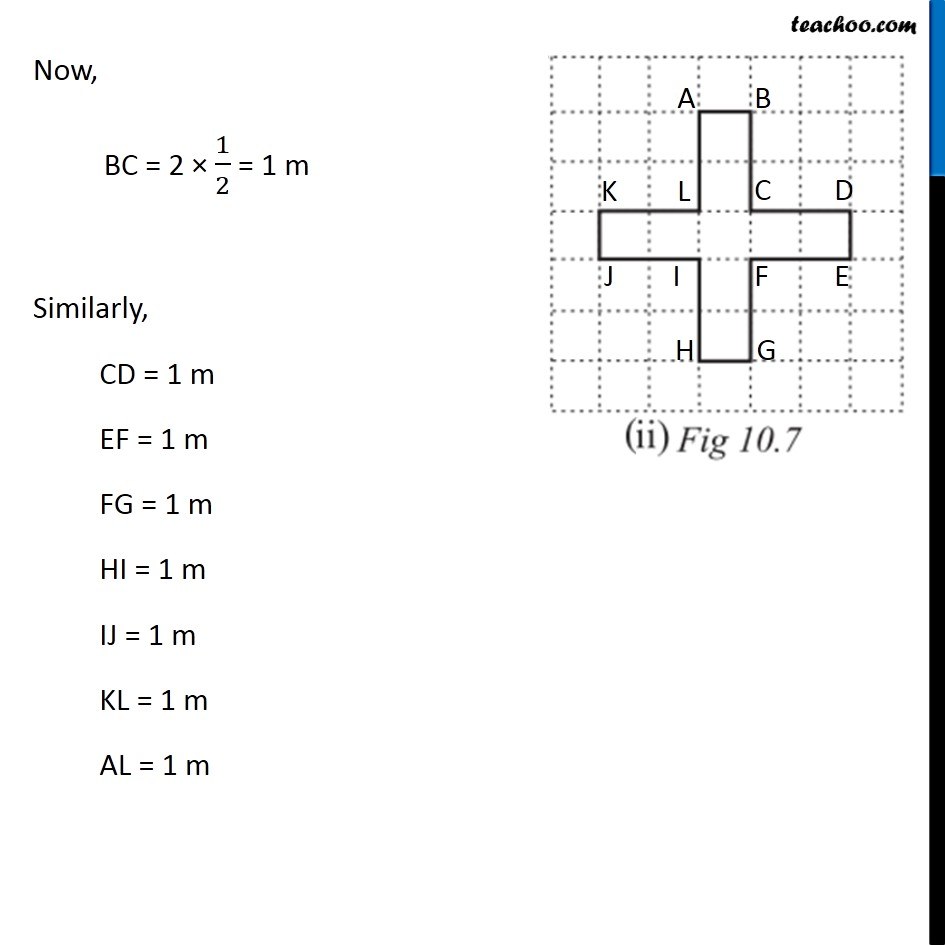
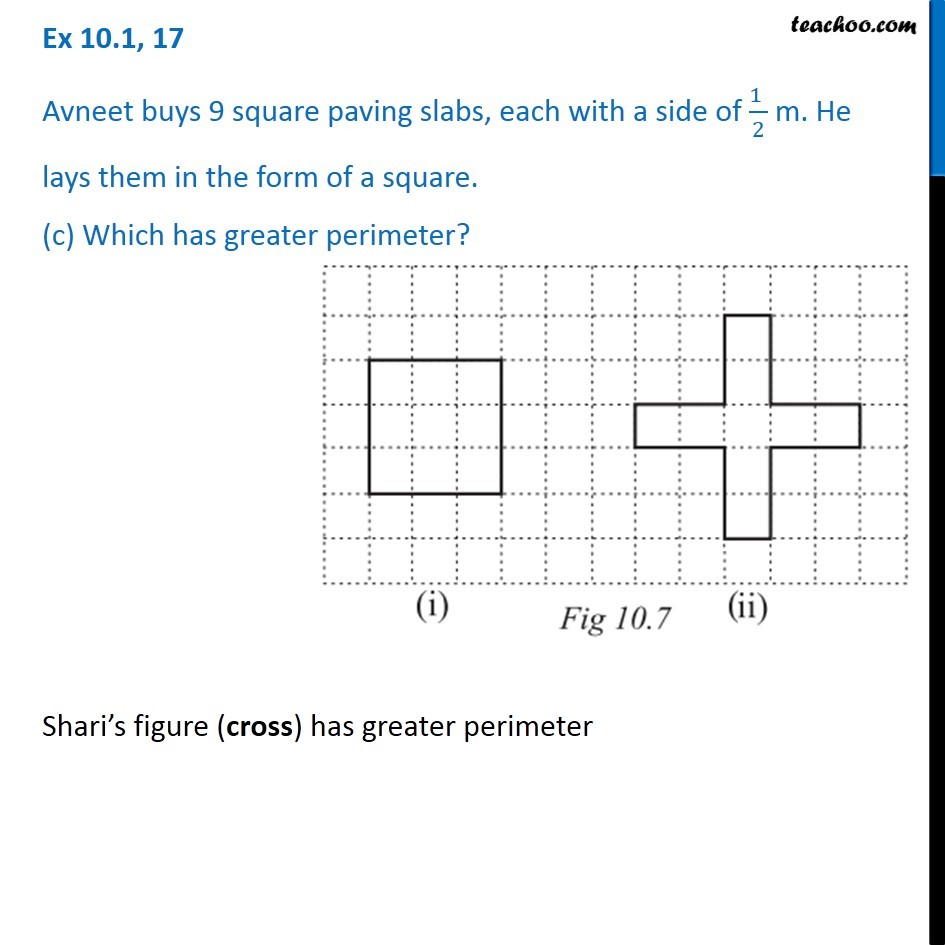
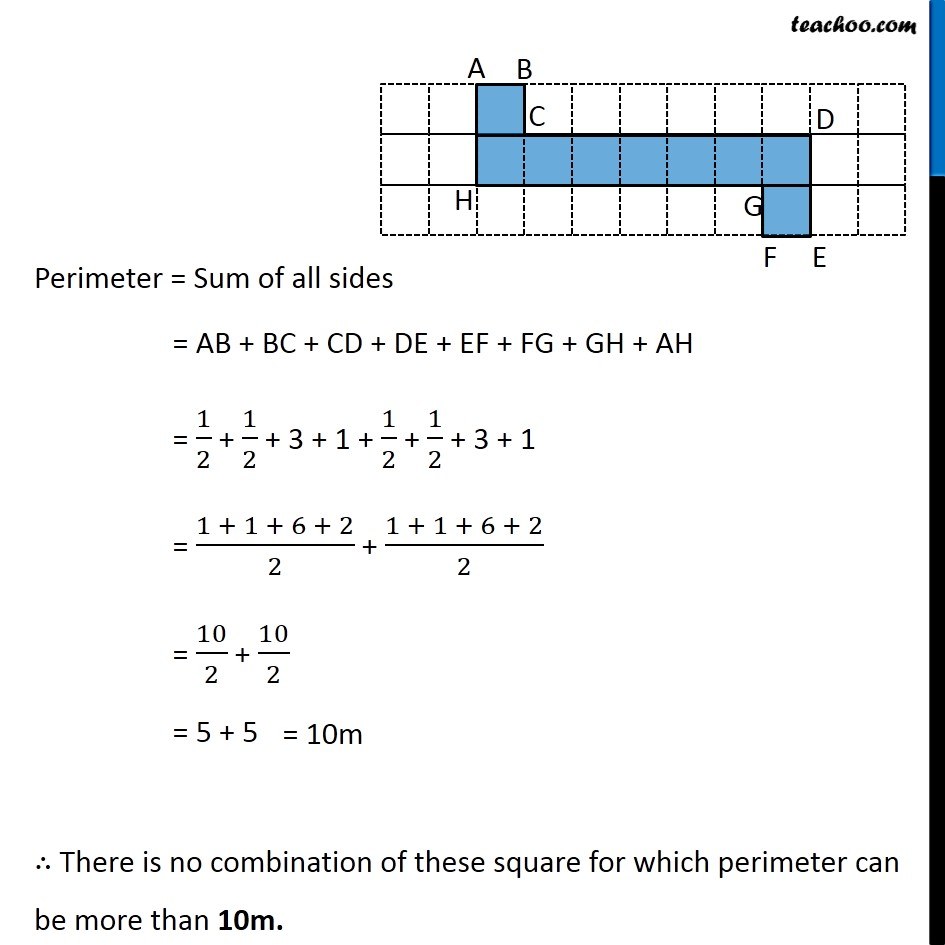
Ex 10.1, 17 Avneet buys 9 square paving slabs, each with a side of (1 )/2 m. He lays them in the form of a square. (a) What is the perimeter of his arrangement [Fig 10.7(i)]? Each side has 3 slabs of sides 1/2 m So, AB = 3 × 1/2 = 3/2 m Similarly, BC = 3/2 m CD = 3/2 m AD = 3/2 m Now, Perimeter = Sum of all sides = AB + BC + CD + AD = 3/2 + 3/2 + 3/2 + 3/2 = (3 + 3 + 3 + 3)/2 Ex 10.1, 17 Avneet buys 9 square paving slabs, each with a side of (1 )/2 m. He lays them in the form of a square. (b) Shari does not like his arrangement. She gets him to lay them out like a cross. What is the perimeter of her arrangement [(Fig 10.7 (ii)]? Here, AB = 1 × 1/2 = 1/2 m Similarly, DE = 1/2 m HG = 1/2 m KJ = 1/2 m Now, BC = 2 × 1/2 = 1 m Similarly, CD = 1 m EF = 1 m FG = 1 m HI = 1 m IJ = 1 m KL = 1 m AL = 1 m Perimeter = Sum of all sides = LA + AB + BC + CD + DE + FE + FG + GH + HI + IJ + JK + KL = 1 + 1/2 + 1 + 1 + 1/2 + 1 + 1 + 1/2 + 1 + 1 + 1/2 + 1 = 4 ("1 + " 1/2 " + 1" ) = 4 × ("2 + " 1/2) = 4 × 5/2 = 2 + 5 = 10 cm Ex 10.1, 17 Avneet buys 9 square paving slabs, each with a side of (1 )/2 m. He lays them in the form of a square. (c) Which has greater perimeter? Shari’s figure (cross) has greater perimeter Ex 10.1, 17 Avneet buys 9 square paving slabs, each with a side of (1 )/2 m. He lays them in the form of a square. (d) Avneet wonders if there is a way of getting an even greater perimeter. Can you find away of doing this? (The paving slabs must meet along complete edges i.e. they cannot be broken.) We need to arrange 9 squares in our grid. Let’s try different figures Here, AB = 9 × 1/2 = 9/2 m CD = 9/2 m AD = 1 × 1/2 = 1/2 m BC = 1 × 1/2 = 1/2 m Perimeter = Sum of all sides = AB + BC + CD + AD = 9/2 + 1/2 + 9/2 + 1/2 = (9 + 1 + 9 + 1)/2 = 20/2 = 10m Another case can be Here, AB = 1 × 1/2 = 1/2 m BC = 1/2 m DE = 1/2 m AF = 2 × 1/2 = 1 m CD = 7 × 1/2 = 7/2 m EF = 8 × 1/2 = 4 m Perimeter = Sum of all sides = AB + BC + CD + DE + EF + AF = 1/2 + 1/2 + 7/2 + 1/2 + 4 + 1 = (1+1+ 7 +1)/2 + 5 = 10/2 + 5 = 5 + 5 = 10 m Another case can be Here, AB = 1 × 1/2 = 1/2 m BC = 1/2 m EF = 1/2 m FG = 1/2 m AH = 2 × 1/2 = 1 m DE = 1 m CD = 6 × 1/2 = 3 m GH = 3 m Perimeter = Sum of all sides = AB + BC + CD + DE + EF + FG + GH + AH = 1/2 + 1/2 + 3 + 1 + 1/2 + 1/2 + 3 + 1 = (1 + 1 + 6 + 2)/2 + (1 + 1 + 6 + 2)/2 = 10/2 + 10/2 = 5 + 5 ∴ There is no combination of these square for which perimeter can be more than 10m.