Question 2 - Compound Interest for fraction years - Chapter 7 Class 8 Comparing Quantities

Transcript

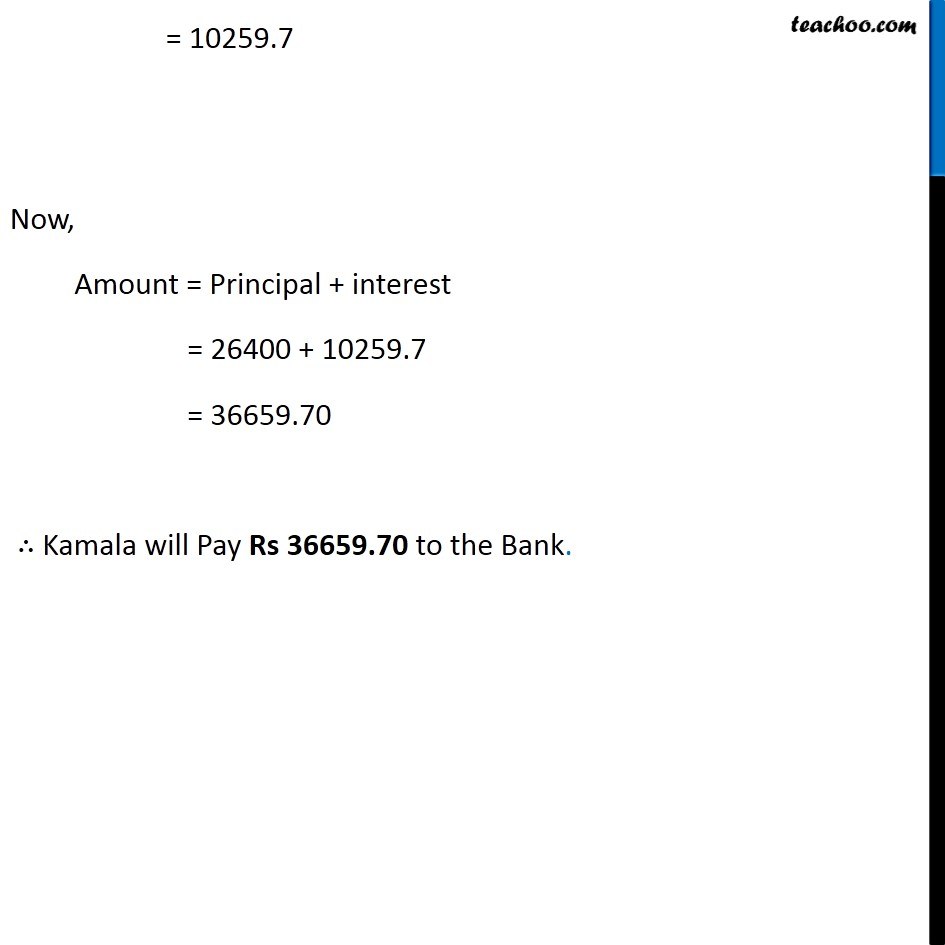
Question 2 Kamala borrowed Rs 26,400 from a Bank to buy a scooter at a rate of 15% p.a. compounded yearly. What amount will she pay at the end of 2 years and 4 months to clear the loan? (Hint: Find A for 2 years with interest is compounded yearly and then find SI on the 2nd year amount for 4/12 years). Given, Principal (P) = 26400 Rate (R) = 15% p.a Time (n) = 2 Years 4 Months = 2 4/12 years = 21/3 years Since n is in fraction We use the formula Compound interest for 2 1/3 years = Compound Interest for 2 years + Simple interest for the next 1/3 years Compound interest for 2 years Principal = 26,400 Rate = 15% Time (n) = 2 Amount = P (1+𝑅/100)^𝑛 = 26400 (1+15/100)^2 = 26400 ((100 + 15)/100)^2 = 26400 (115/100)^2 = 26400 × ((115 × 115)/(100 ×100))^2 = 264 × 13225/100 = (264 × 13225)/100 = 3491400/100 = 34914 ∴ Amount = Rs 34914 Now, Amount = Principal + Interest 34914 = 26400 + Interest 34914 − 26400 = Interest 8514 = Interest ∴ Interest = 8514 ∴ Interest for 2 years = Rs 8514 & Amount after 2 years = Rs 34914 Simple interest for next 𝟏/𝟑 year Principal will be the amount after 1 year P = Rs 34914 R = 15% p.a T = 1/3 years SI = 𝑃𝑅𝑇/100 = (34914 × 15 × 1/3 )/100 = (34914 ×15)/(100 × 3) = (34914 × 5)/100 = 34914/20 = 17457/10 = 1745.7 ∴ Simple interest for 1/3 years = Rs 1745.7 Now, Compound Interest for 2 1/3 years = Compound Interest for 2 years + Simple interest for 1/3 year = 8514 + 1745.7 = 10259.7 Now, Amount = Principal + interest = 26400 + 10259.7 = 36659.70 ∴ Kamala will Pay Rs 36659.70 to the Bank.