

Constructing Special Quadrilaterals
Last updated at Dec. 16, 2024 by Teachoo








Transcript
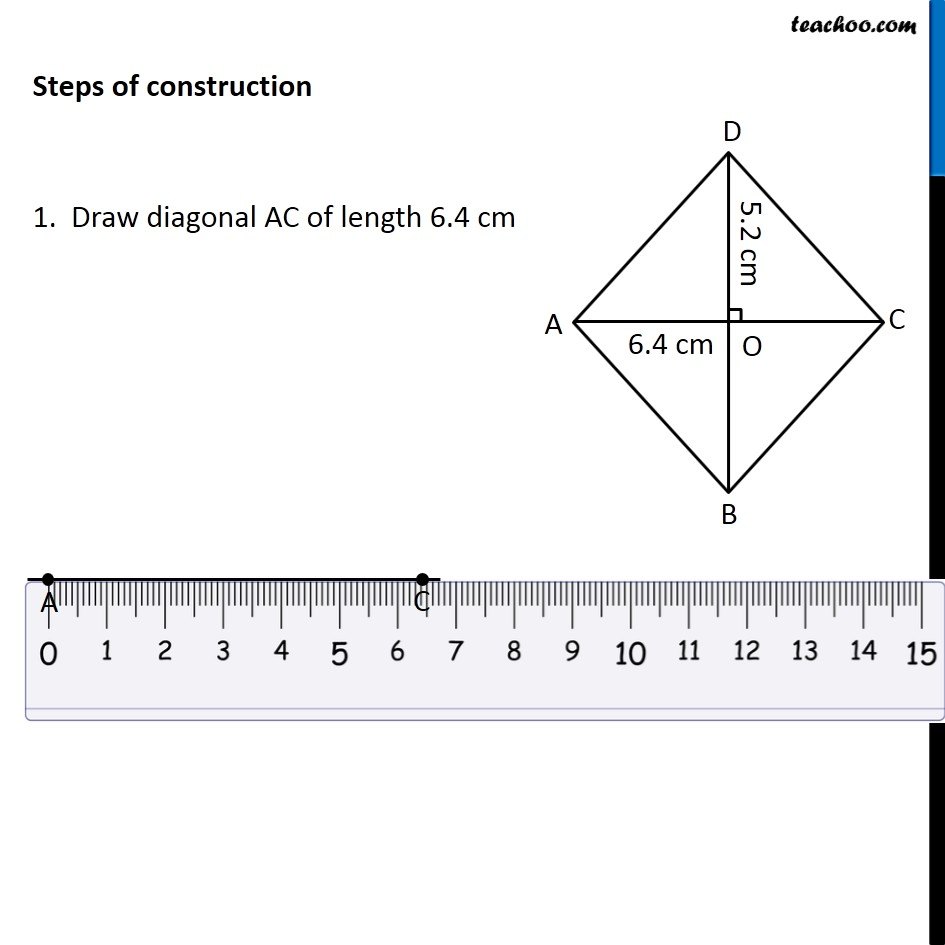
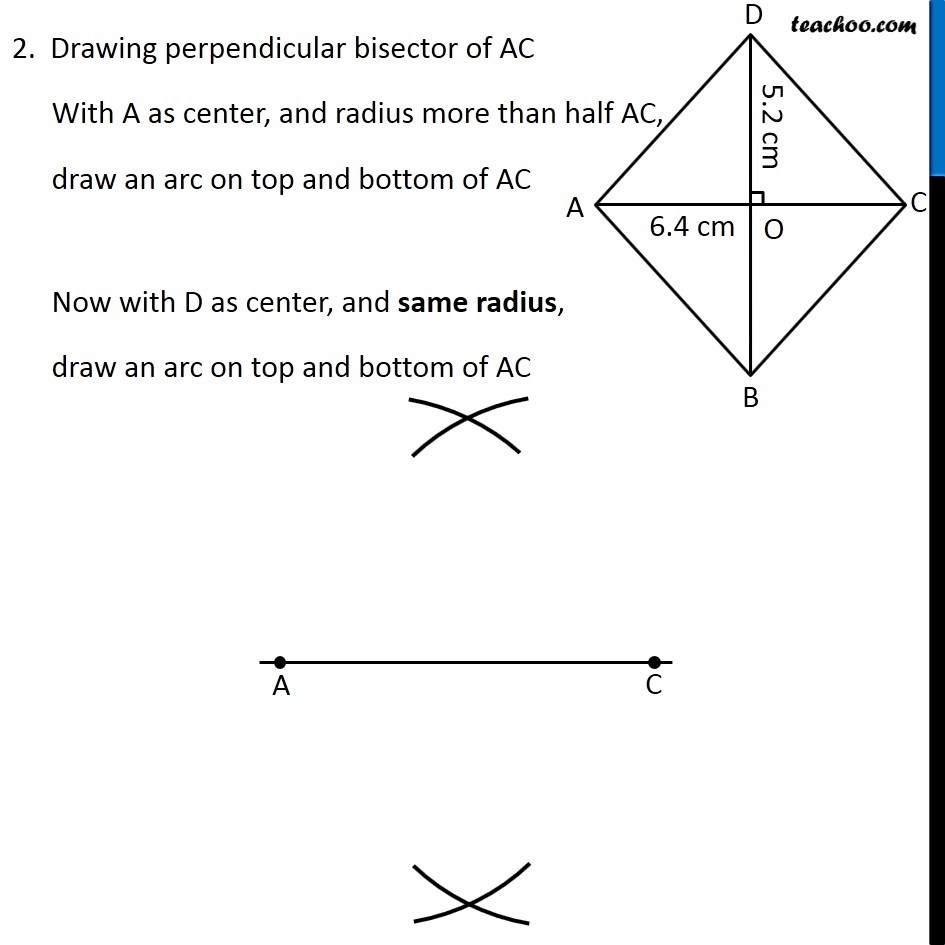
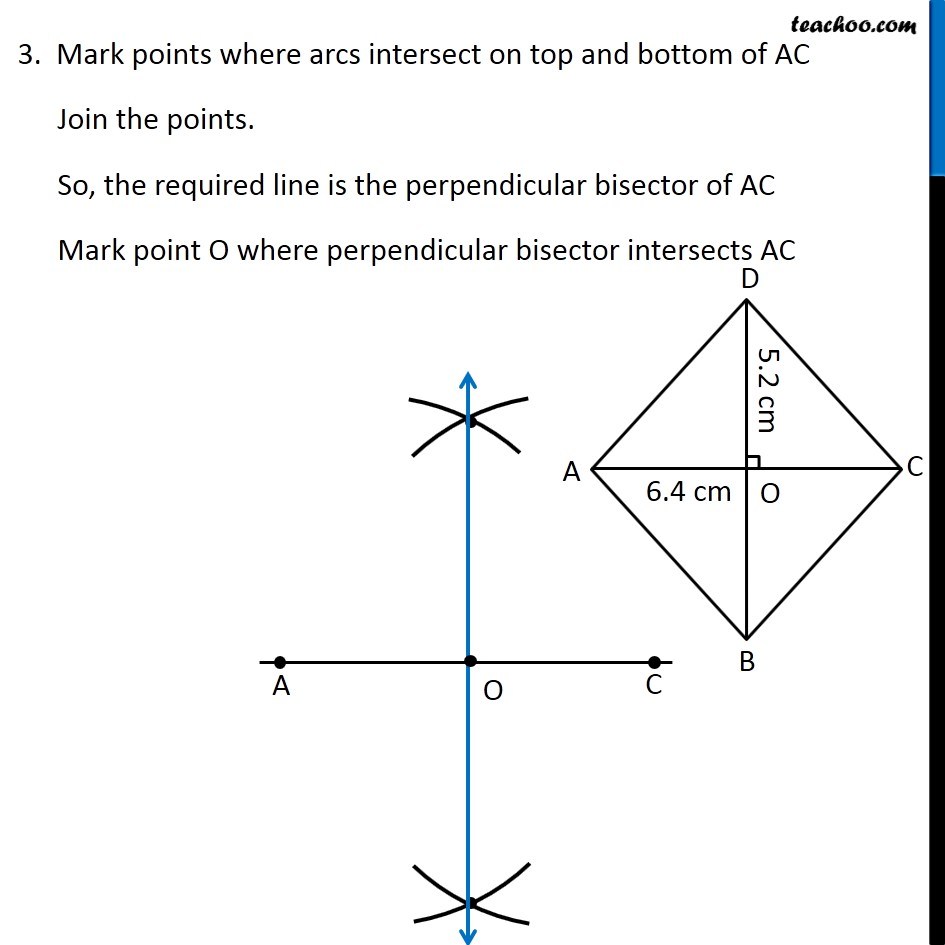
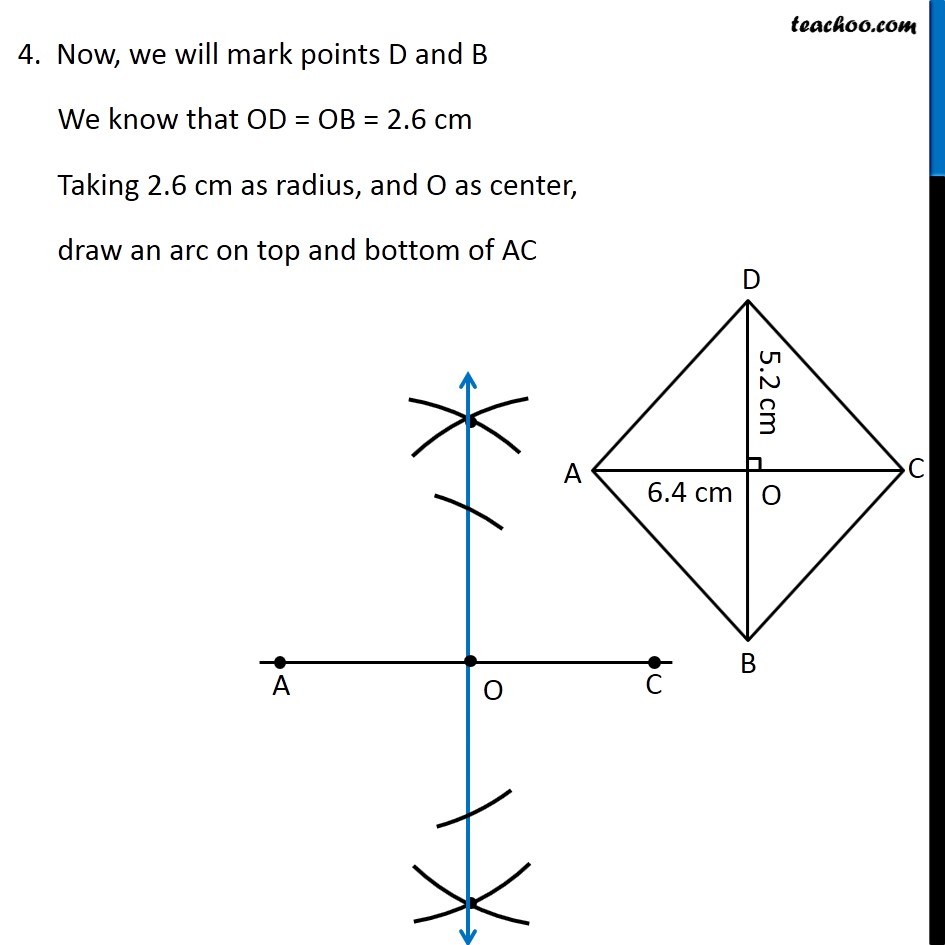
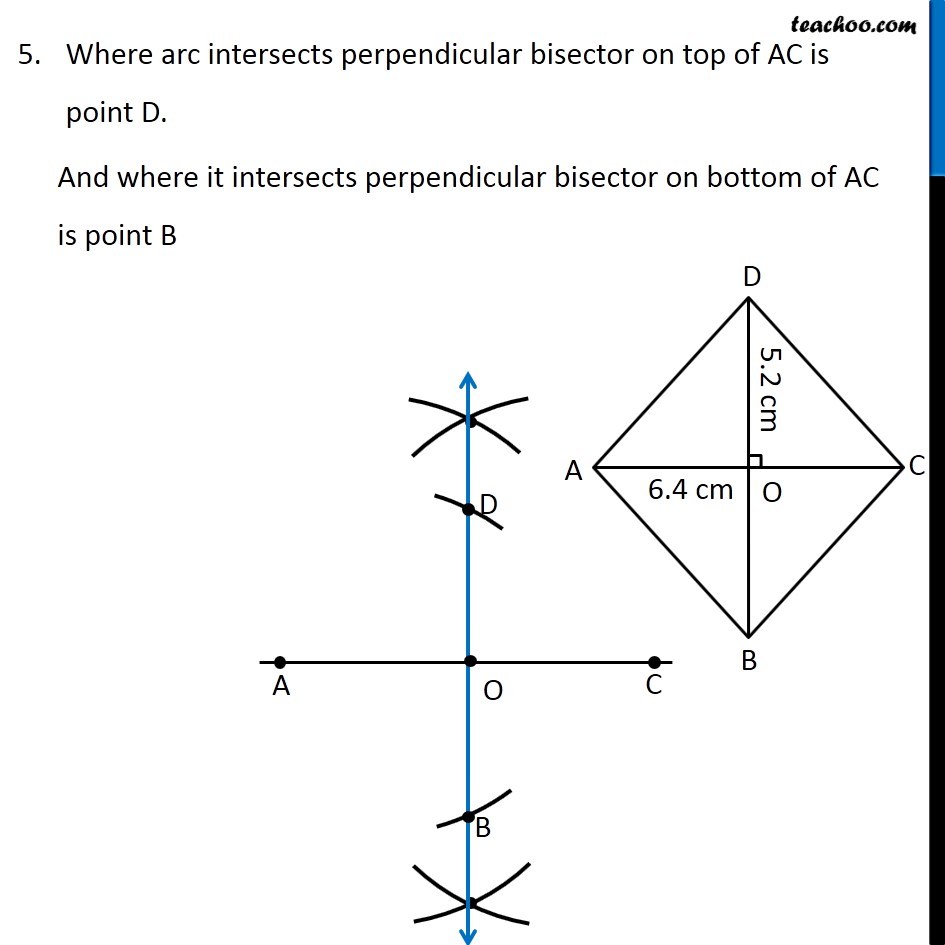
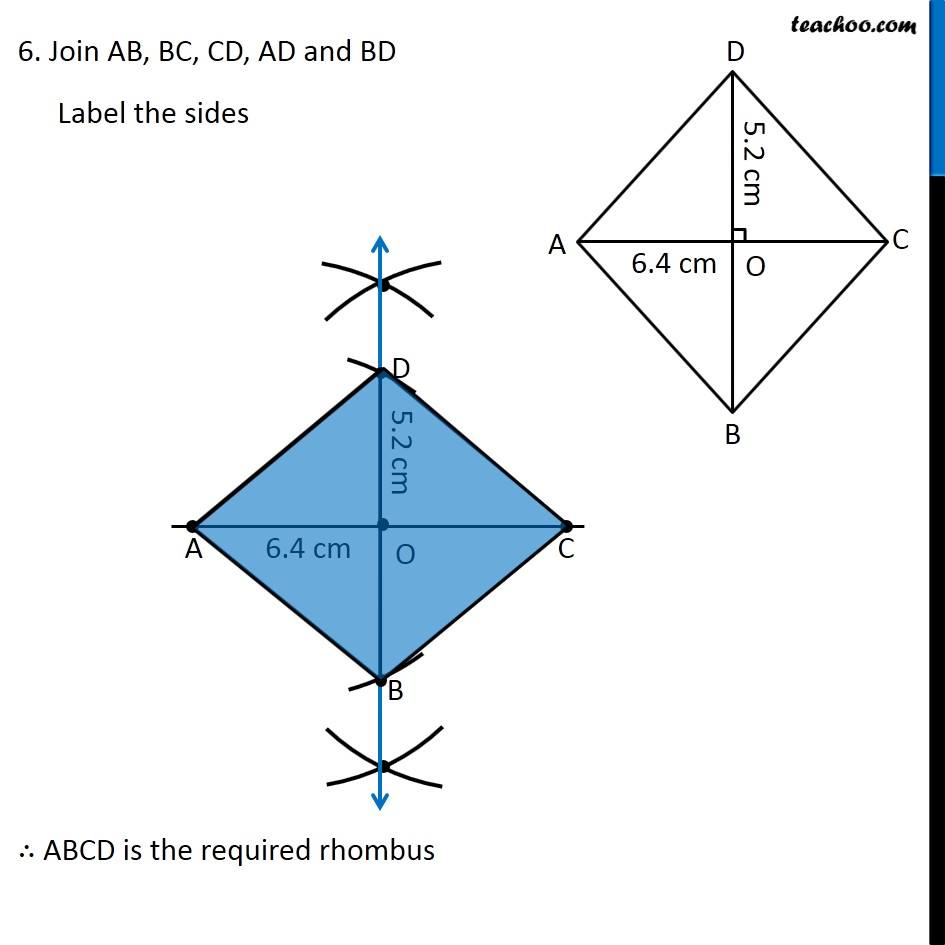
Question 2 Draw the following. A rhombus whose diagonals are 5.2 cm and 6.4 cm long. Here, we are given a rhombus with both diagonals To construct it, we will use property of rhombus In rhombus, Diagonals are perpendicular bisectors of each other So, our figure will look like Here, BD is the perpendicular bisector of AC So, BD ⊥ AC and O is the mid-point of AC and BD ∴ OD = OB = (5.2 𝑐𝑚)/2 = 2.6 cm To construct it, we will first draw AC, then perpendicular bisector of AC Then, we will mark OD = 2.6 cm and OB = 2.6 cm on the perpendicular bisector. Let’s construct it Steps of construction 1. Draw diagonal AC of length 6.4 cm 2. Drawing perpendicular bisector of AC With A as center, and radius more than half AC, draw an arc on top and bottom of AC Now with D as center, and same radius, draw an arc on top and bottom of AC 3. Mark points where arcs intersect on top and bottom of AC Join the points. So, the required line is the perpendicular bisector of AC Mark point O where perpendicular bisector intersects AC 4. Now, we will mark points D and B We know that OD = OB = 2.6 cm Taking 2.6 cm as radius, and O as center, draw an arc on top and bottom of AC Where arc intersects perpendicular bisector on top of AC is point D. And where it intersects perpendicular bisector on bottom of AC is point B 6. Join AB, BC, CD, AD and BD Label the sides ∴ ABCD is the required rhombus