
Ex 3.4
Last updated at Dec. 16, 2024 by Teachoo




Transcript
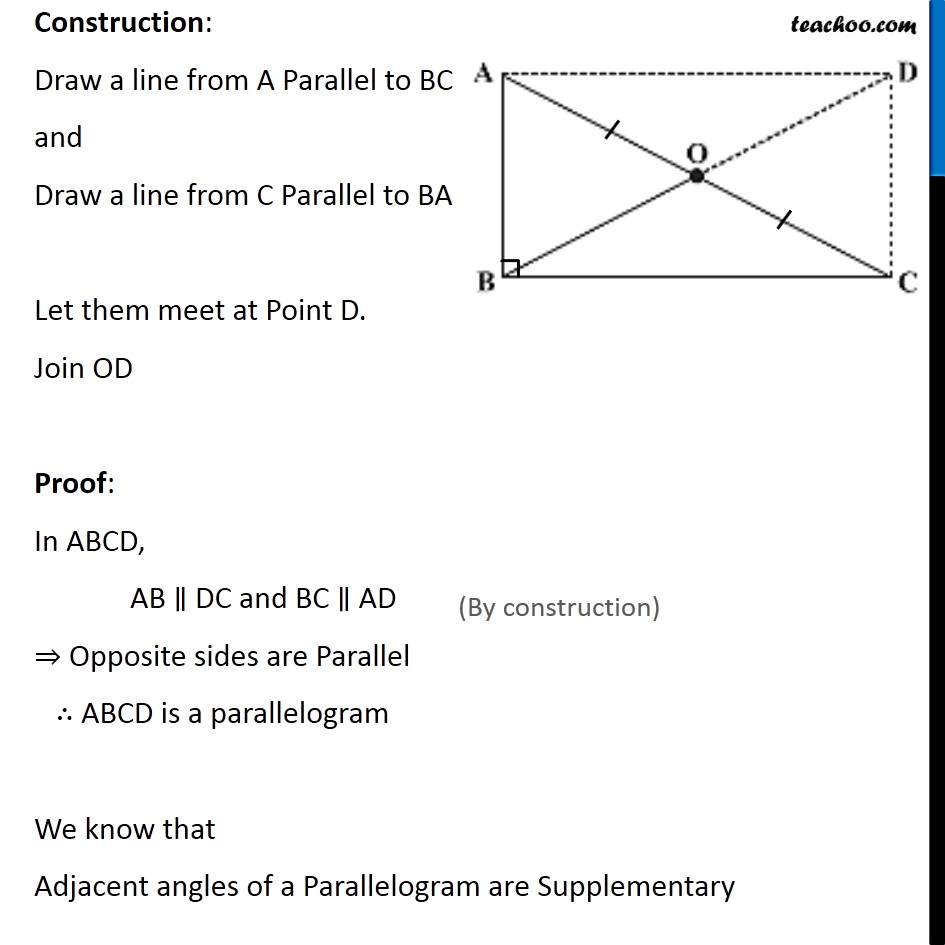
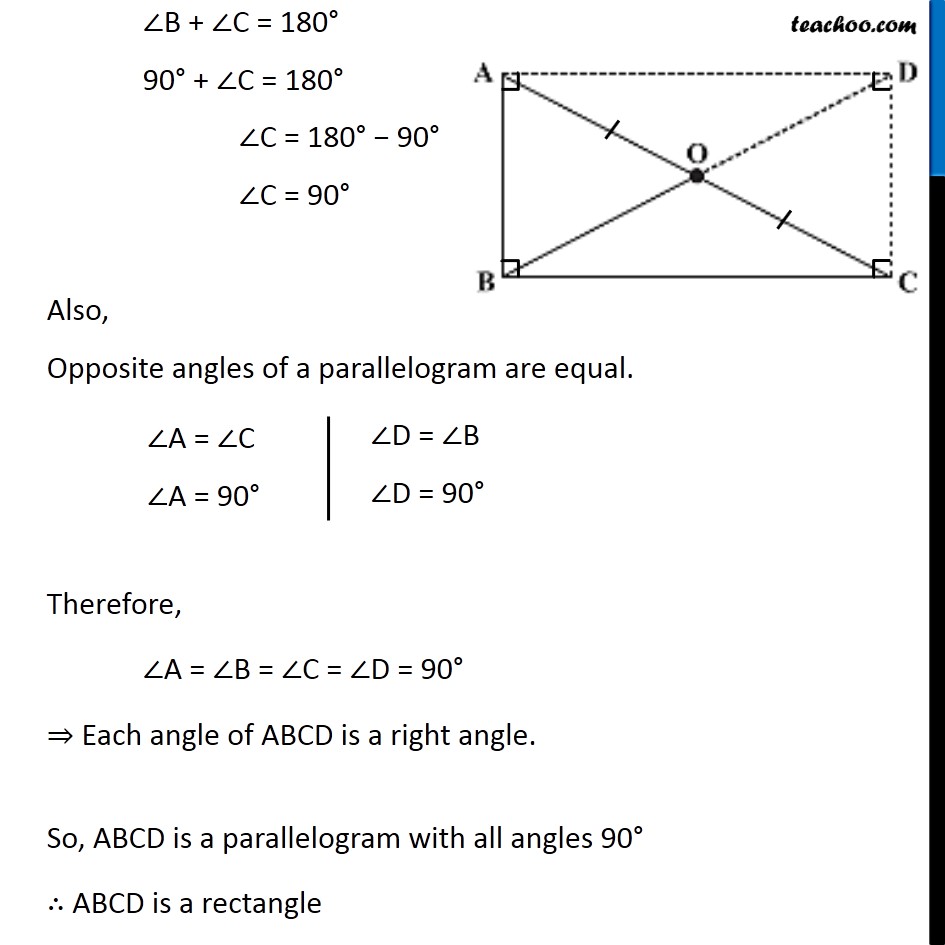
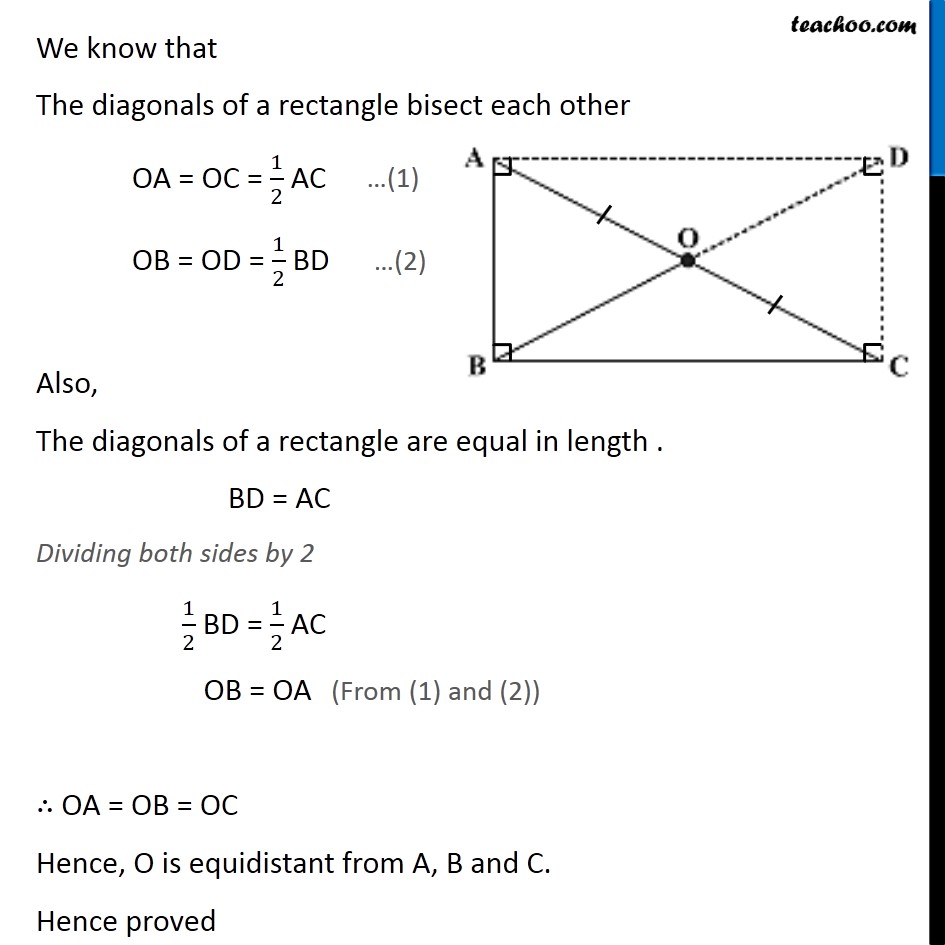
Ex 3.4, 6 ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you). Given: A Right-angled triangle ABC. O is the mid-point of AC. To Prove: O is equidistant from A, B and C i.e. OA = OB = OC Construction: Draw a line from A Parallel to BC and Draw a line from C Parallel to BA Let them meet at Point D. Join OD Proof: In ABCD, AB ∥ DC and BC ∥ AD ⇒ Opposite sides are Parallel ∴ ABCD is a parallelogram We know that Adjacent angles of a Parallelogram are Supplementary ∠B + ∠C = 180° 90° + ∠C = 180° ∠C = 180° − 90° ∠C = 90° Also, Opposite angles of a parallelogram are equal. ∠A = ∠C ∠A = 90° Therefore, ∠A = ∠B = ∠C = ∠D = 90° ⇒ Each angle of ABCD is a right angle. So, ABCD is a parallelogram with all angles 90° ∴ ABCD is a rectangle We know that The diagonals of a rectangle bisect each other OA = OC = 1/2 AC OB = OD = 1/2 BD Also, The diagonals of a rectangle are equal in length . BD = AC Dividing both sides by 2 1/2 BD = 1/2 AC OB = OA ∴ OA = OB = OC Hence, O is equidistant from A, B and C. Hence proved