Question 2 - Polygons - Chapter 3 Class 8 Understanding Quadrilaterals

Transcript

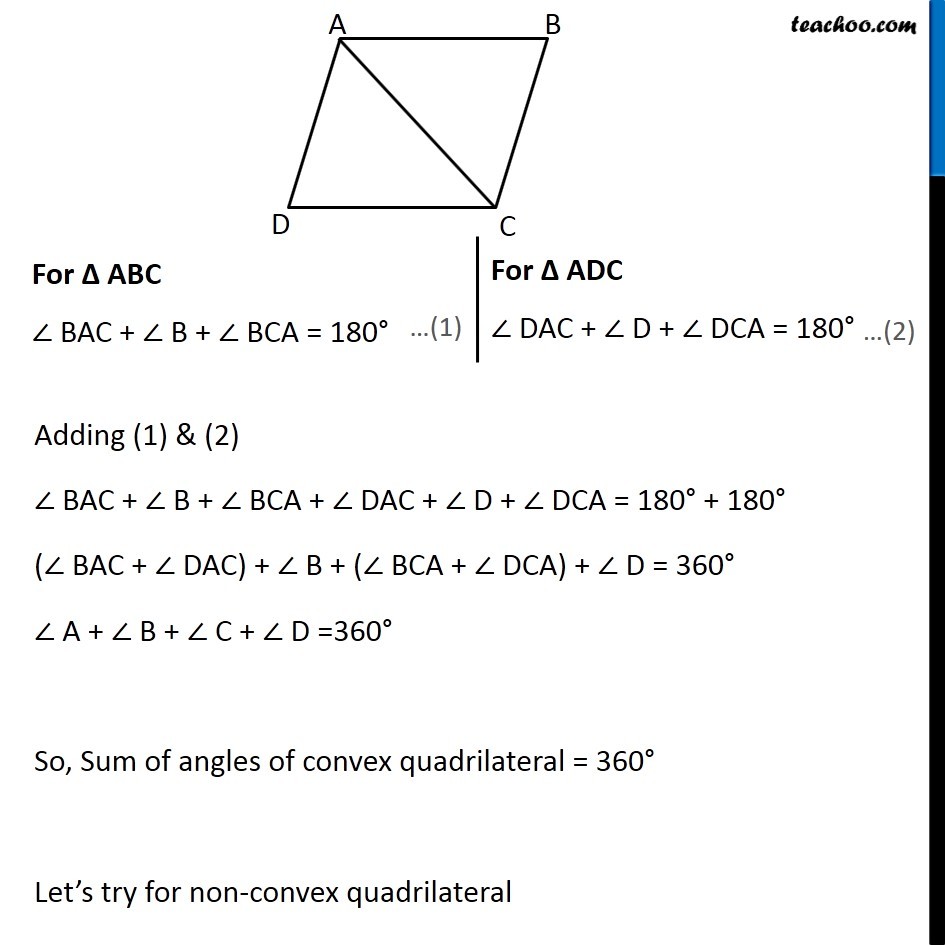
Question 2 What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!) Convex Quadrilateral In Quadrilateral ABCD Sum of Angles of ABCD = ∠ A + ∠ B + ∠ C + ∠ D Let’s divide Quadrilateral ABCD into two triangles – Δ ABC & Δ ADC Now, We know that Sum of angles of a triangle is 180° For Δ ABC ∠ BAC + ∠ B + ∠ BCA = 180° For Δ ADC ∠ DAC + ∠ D + ∠ DCA = 180° Adding (1) & (2) ∠ BAC + ∠ B + ∠ BCA + ∠ DAC + ∠ D + ∠ DCA = 180° + 180° (∠ BAC + ∠ DAC) + ∠ B + (∠ BCA + ∠ DCA) + ∠ D = 360° ∠ A + ∠ B + ∠ C + ∠ D =360° So, Sum of angles of convex quadrilateral = 360° Let’s try for non-convex quadrilateral Non-Convex Quadrilateral In Quadrilateral ABCD Sum of Angles of ABCD = ∠ A + ∠ B + ∠ C + ∠ D Let’s divide Quadrilateral ABCD into two triangles – Δ ABC & Δ ADC Now, We know that Sum of angles of a triangle is 180° For Δ ABC ∠ BAC + ∠ B + ∠ BCA = 180° For Δ ADC ∠ DAC + ∠ D + ∠ DCA = 180° Adding (1) & (2) ∠ BAC + ∠ B + ∠ BCA + ∠ DAC + ∠ D + ∠ DCA = 180° + 180° (∠ BAC + ∠ DAC) + ∠ B + (∠ BCA + ∠ DCA) + ∠ D = 360° ∠ A + ∠ B + ∠ C + ∠ D =360° So, Sum of angles of non-convex quadrilateral = 360° Hence, sum of angles is same for both convex and non-convex quadrilaterals.