Question 6 - Manufacturing problems - Chapter 12 Class 12 Linear Programming

Transcript

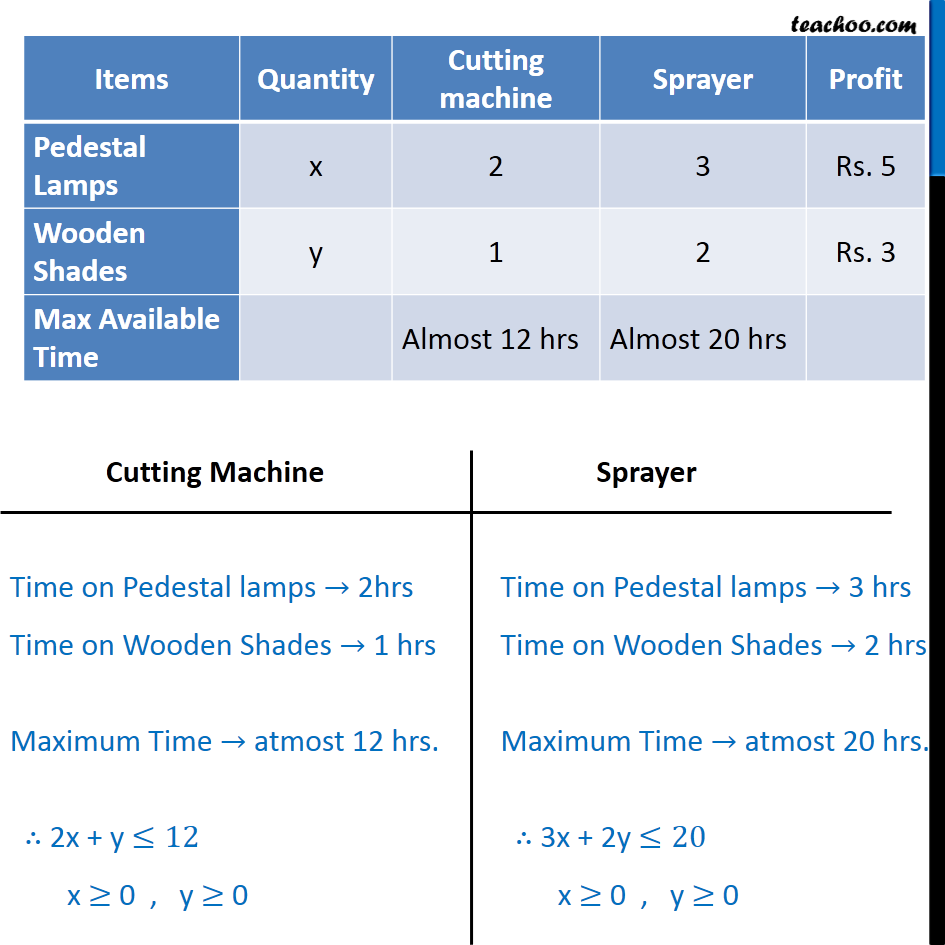
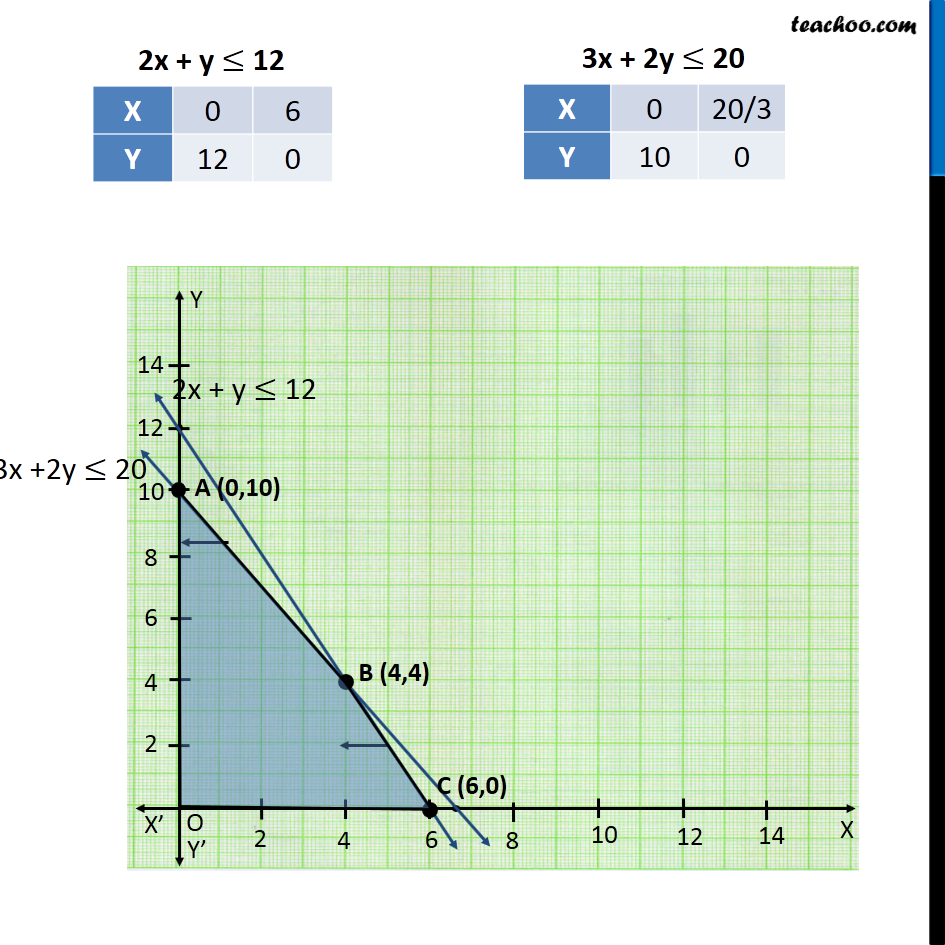
Question 6 A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayerto manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximise his profit? Let the number of pedestal lamps be x and number of wooden shades be y As, we want to maximize the profit, the function used here is Maximize Z Profile On Pedestal lamps → Rs 5 Profile On Wooden Shades → Rs 3 Maximize Z = 5x + 3y Combining all Constraints: Maximize Z = 5x + 3y Subject to Constraints 2x + y ≤ 12 3x + 2y ≤ 20 x ≥ 0 , y ≥ 0 ∴ The profit will be maximum if, Number of lamps → 4 Number of Wooden Shades → 4 Maximum profit → Rs 32