



Last updated at Dec. 16, 2024 by Teachoo





Transcript
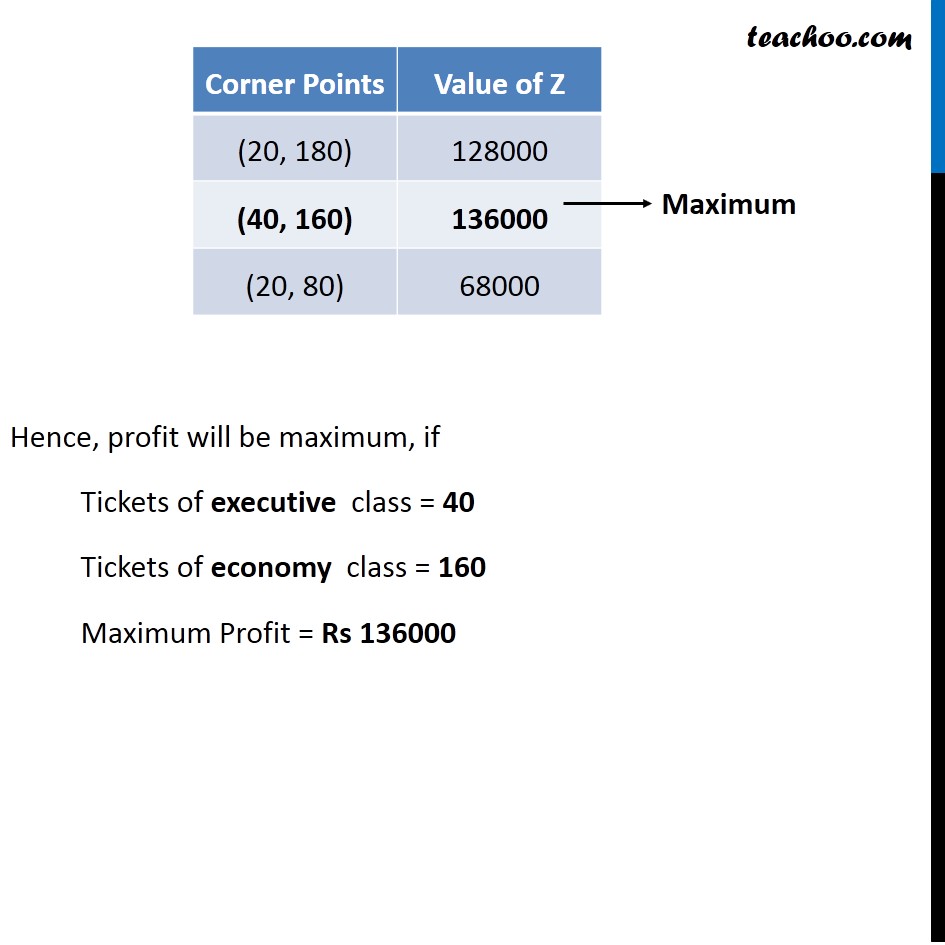
Misc 5 An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?Let number of Executive class air ticket sold be x number of Economy class air ticket sold be y According to Question : Maximum Seating capacity is 200 ∴ x + y ≤ 200 Atleast 20 tickets are reserved for executive class ∴ x ≥ 20 Number of tickets of economy class should be atleast 4 times the Executive class ∴ y ≥ 4x y − 4x ≥ 0 As, we need to maximize the Profit, hence the function used is Maximize Z. Profit on executive class = Rs 1000 Profit on economy class = Rs 600 ∴ Maximize Z = 1000x + 600y Combining all Constraints : Max. Z = 1000x + 600y x + y ≤ 200 x ≥ 20 y − 4x ≥ 0 x ≥ 0, y ≥ 0 Hence, profit will be maximum, if Tickets of executive class = 40 Tickets of economy class = 160 Maximum Profit = Rs 136000