Question 6 - Transport problems - Chapter 12 Class 12 Linear Programming

Transcript

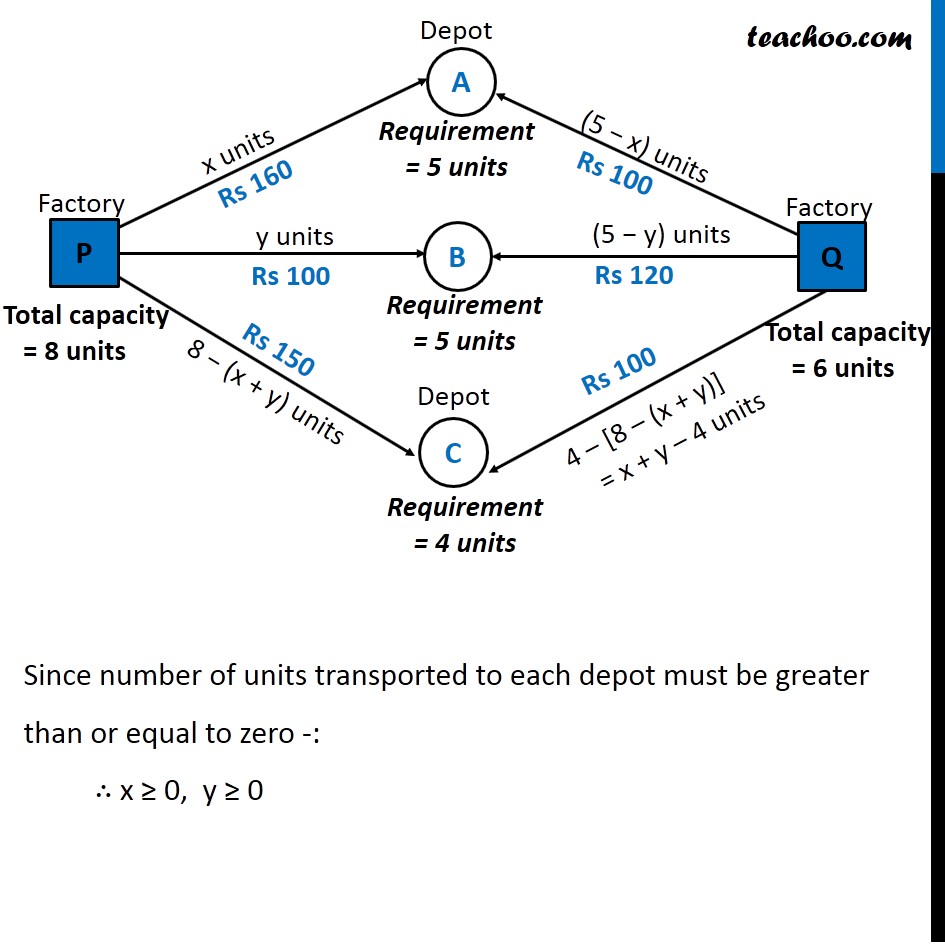
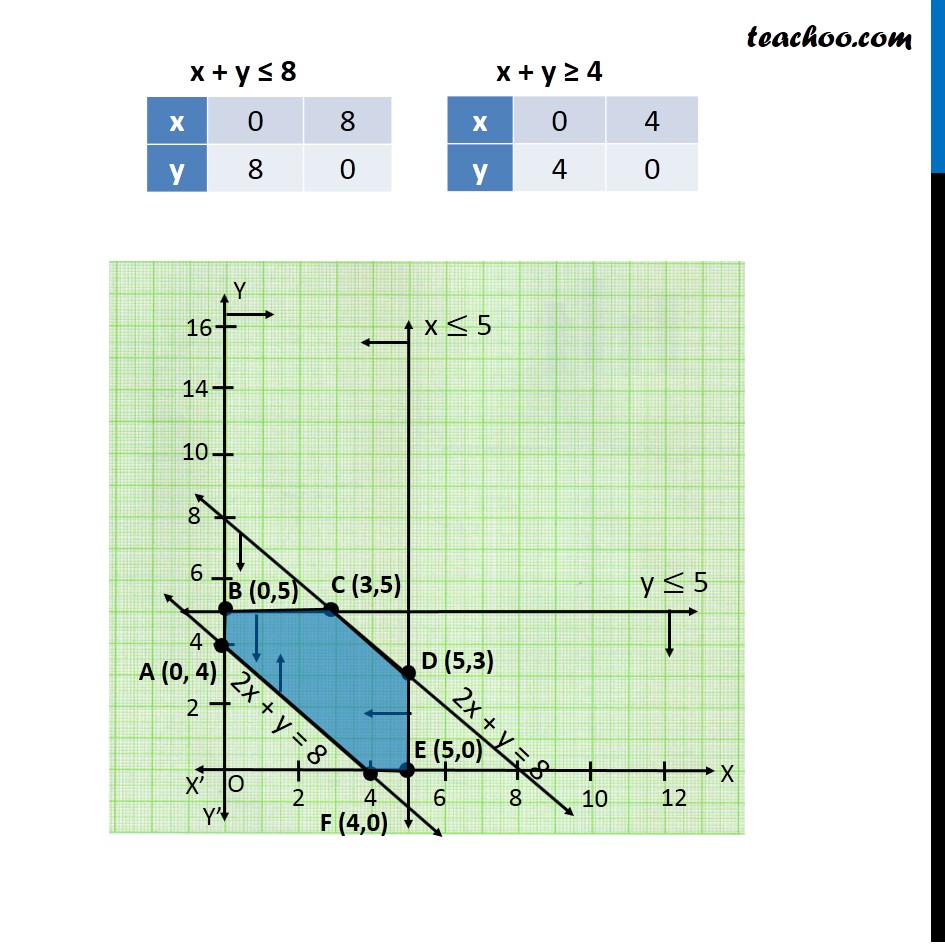
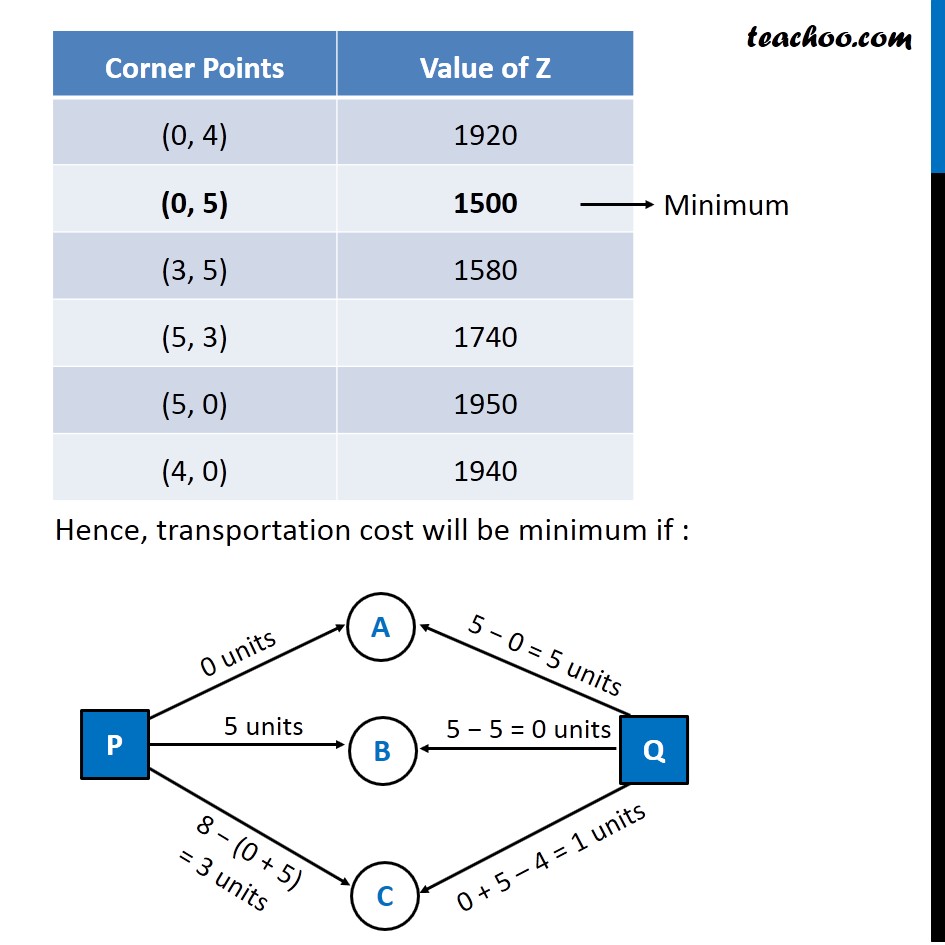
Question 6 (Transportation problem) There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units. The cost of transportation per unit is given below: How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost? Let P transport x units to Depot A P transport y units to Depot B Since number of units transported to each depot must be greater than or equal to zero -: ∴ x ≥ 0, y ≥ 0 8 − (x + y) ≥ 0 x + y ≤ 8 5 – x ≥ 0 x ≤ 5 5 − y ≥ 0 y ≤ 5 x + y − 4 ≥ 0 x + y ≥ 4 As we need to minimize the cost of transportation, Hence the function used is minimize Z. Total transportation cost will be Z = 160 x + 100y + 150 [8 − x + y] + 100 (5 – x) + 120 (5 − y) + 100 (x + y − 4) Z = 10 x − 70y + 1900 Combining all constraints : Min, Z = 10x − 70y + 1900 Subject to constraints : x + y ≤ 8 x ≤ 5 y ≤ 5 x + y ≥ 4 x ≥ 0 , y ≥ 0 Hence, transportation cost will be minimum if : Minimum Cost = Rs 1550 From P : 0, 5, 3 units to depots A, B, C respectively From Q : 5, 0, 1 units to depots A, B, C respectively