Question 5 - Manufacturing problems - Chapter 12 Class 12 Linear Programming

Transcript

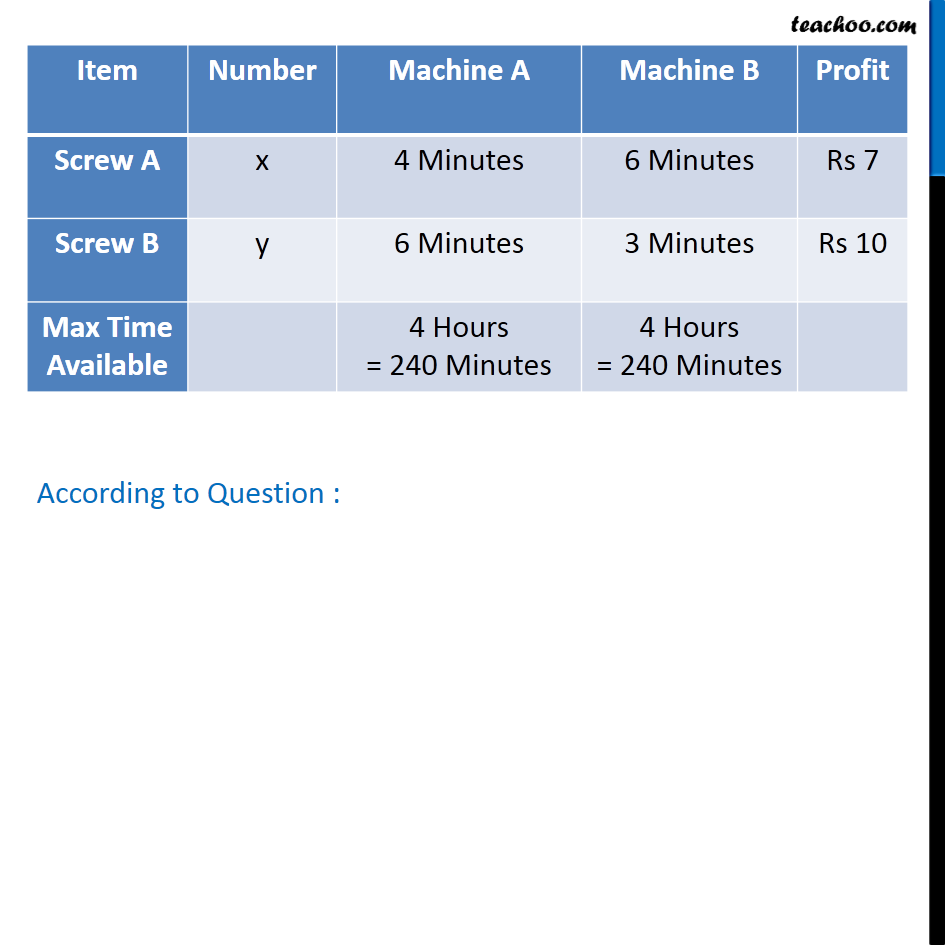
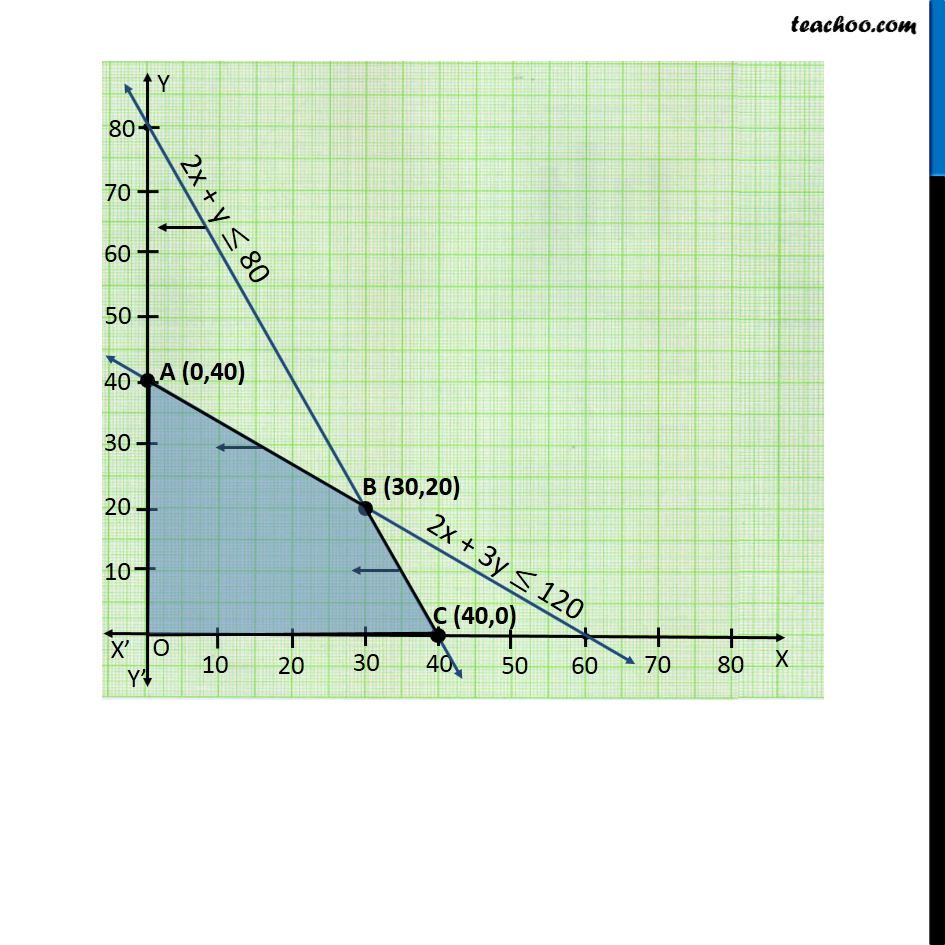
Question 5 A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package of screws A, while it takes 6 minutes on automatic an 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximise his profit? Determine the maximum profit. Let the number of packages of Screw A be x number of packages of screw B be y. According to Question : As, we need to Maximize the Profit, the Function used here is Maximize Z. Profit on Screw A Rs 7 Profit on Screw B Rs 10 Maximize Z = 7x + 10y Combining all Constraints Max Z = 7x + 10y Subject to constraints : 2x + 3y 120 2x + y 80 x 0, y 0. Hence, Profit will be maximum if the Company produces : 30 packages of Screw A 20 packages of Screw B Maximum Profit = Rs 410