Question 7 - Area between curve and line - Chapter 8 Class 12 Application of Integrals

Transcript

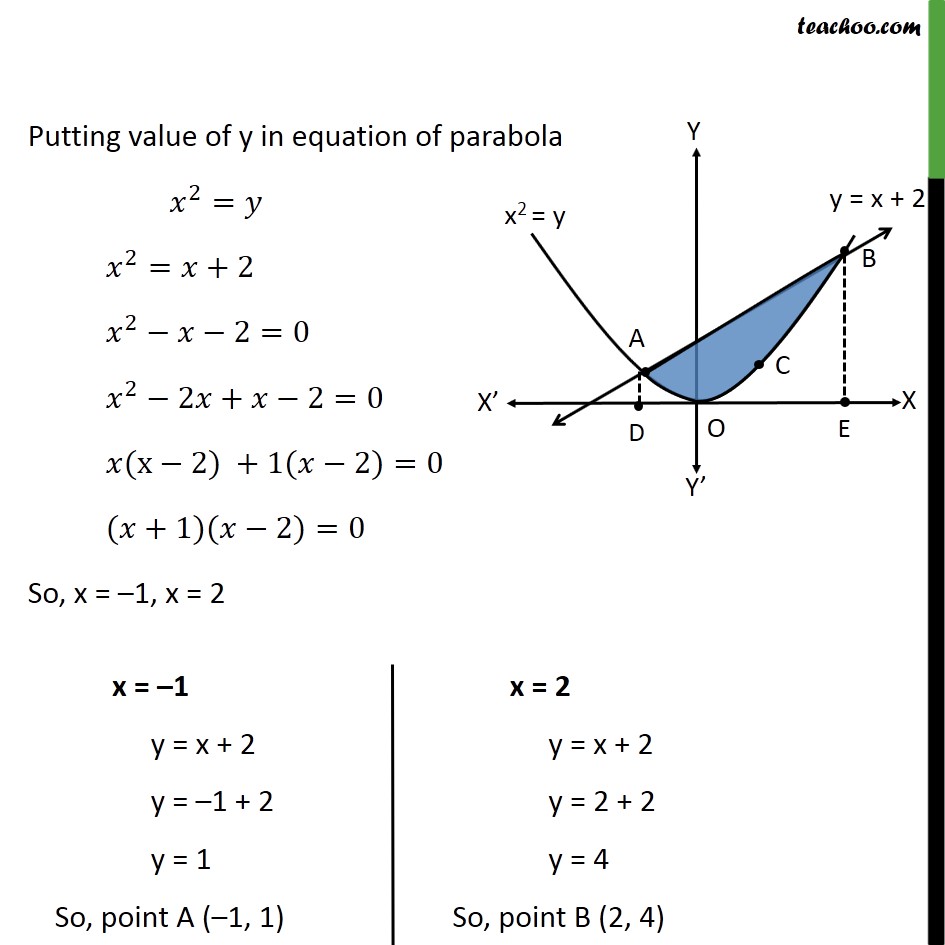
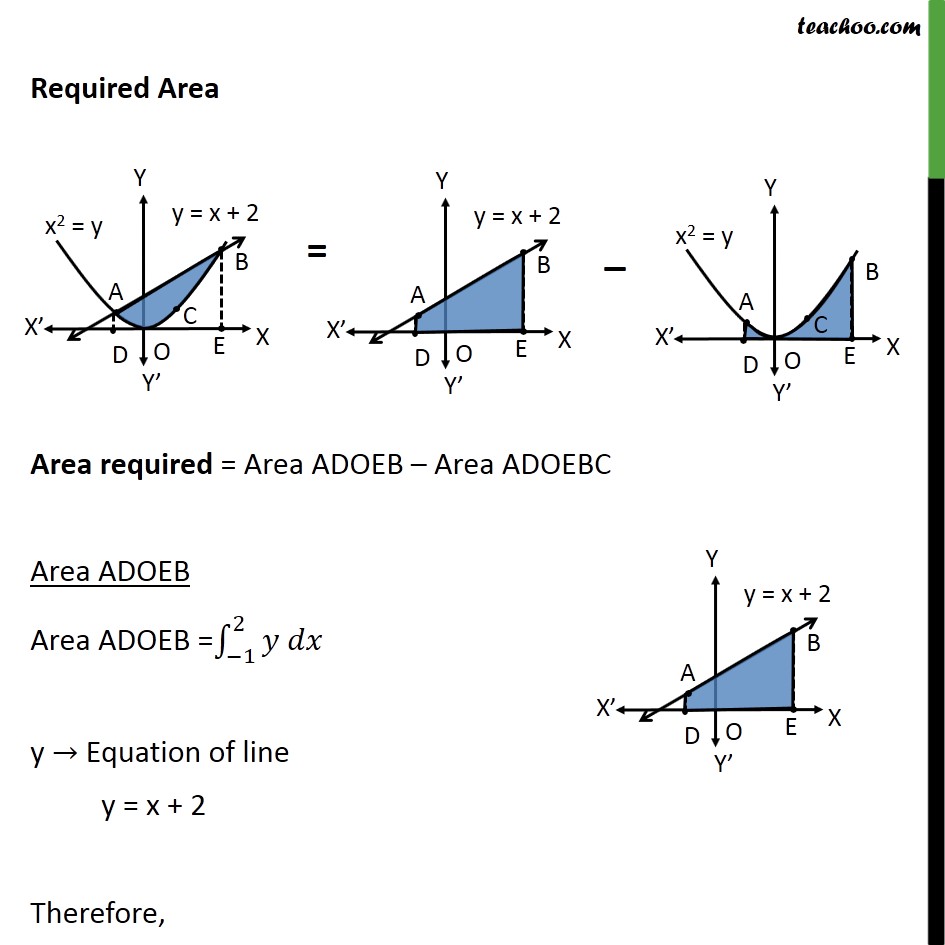
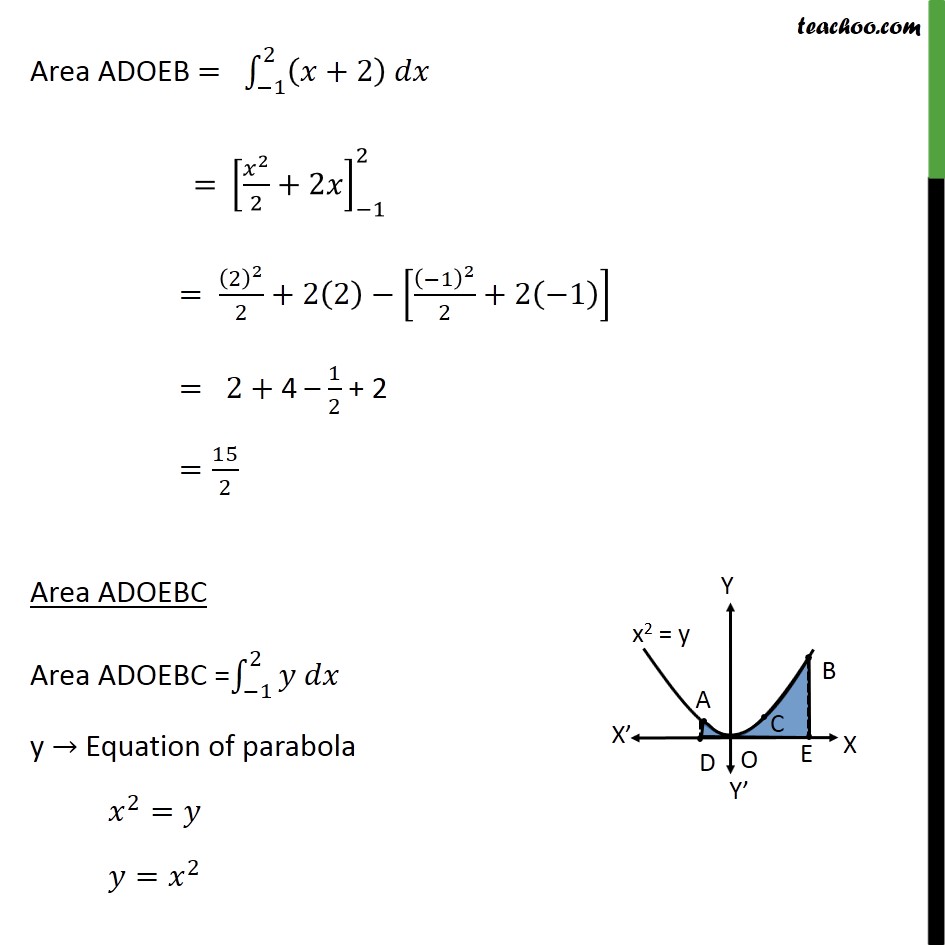
Question 7 Find the area of the region enclosed by the parabola 𝑥﷮2﷯=𝑦, the line 𝑦=𝑥+2 and the 𝑥−axis Step 1: Draw the Figure Parabola is 𝑥﷮2﷯=𝑦 Also, 𝑦=𝑥+2 is a straight line Step 2: Finding point of intersection A & B Equation of line is 𝑦=𝑥+2 Putting value of y in equation of parabola 𝑥﷮2﷯=𝑦 𝑥﷮2﷯=𝑥+2 𝑥﷮2﷯−𝑥−2=0 𝑥﷮2﷯−2𝑥+𝑥−2=0 𝑥(x−2) +1(𝑥−2)=0 (𝑥+1)(𝑥−2)=0 So, x = –1, x = 2 Required Area Area required = Area ADOEB – Area ADOEBC Area ADOEB Area ADOEB = −1﷮2﷮𝑦 𝑑𝑥﷯ y → Equation of line y = x + 2 Therefore, Area ADOEB = −1﷮2﷮ 𝑥+2﷯ 𝑑𝑥﷯ = 𝑥﷮2﷯﷮2﷯+2𝑥﷯﷮−1﷮2﷯ = 2﷯﷮2﷯﷮2﷯+2 2﷯− −1﷯﷮2﷯﷮2﷯+2 −1﷯﷯ = 2+ 4 – 1﷮2﷯ + 2 = 15﷮2﷯ Area ADOEBC Area ADOEBC = −1﷮2﷮𝑦 𝑑𝑥﷯ y → Equation of parabola 𝑥﷮2﷯=𝑦 𝑦= 𝑥﷮2﷯ Therefore, Area ADOEBC = −1﷮2﷮ 𝑥﷮2﷯ 𝑑𝑥﷯ = 𝑥﷮3﷯﷮3﷯﷯﷮−1﷮2﷯ = 1﷮3﷯ 2﷯﷮3﷯− −1﷯﷮3﷯﷯ = 9﷮3﷯ = 3 Area required = Area ADOEB – Area ADOEBC = 15﷮2﷯ – 3 = 9﷮2﷯