





Limits - Of Trignometric functions
Last updated at Dec. 16, 2024 by Teachoo







Transcript
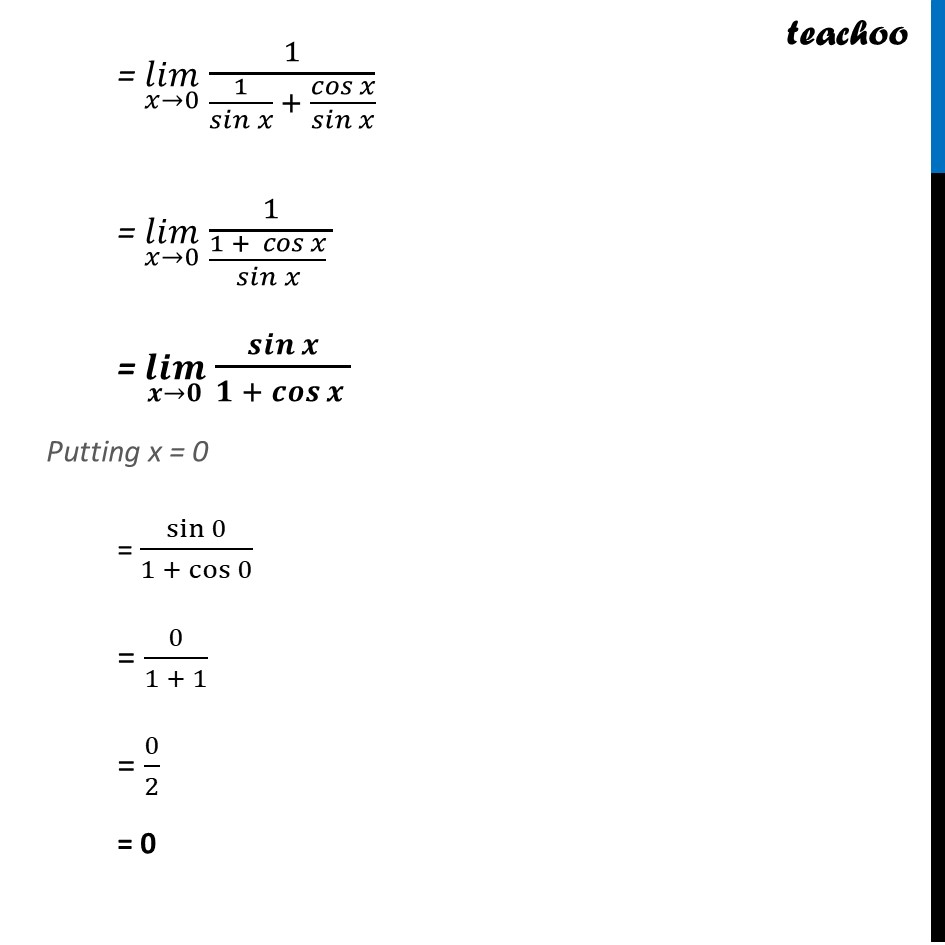
Ex 12.1, 21 (Method 1) Evaluate the Given limit: lim┬(x→0) (cosec x – cot x) lim┬(x→0) (cosec x – cot x) = lim┬(x→0) (1/sin𝑥 −cos𝑥/sin𝑥 ) = lim┬(x→0) (1 −〖 cos〗𝑥)/sin〖𝑥 〗 Putting x = 0 = (1 − cos〖0 〗)/sin0 = (1 − 1)/0 = 0/0 Using cosec θ = (1 )/(sin θ) cot θ = (cos θ)/(sin θ) Since it is coming 0/0 Hence, we need to simplify lim┬(x→0) (1 −〖 cos〗𝑥)/sin〖𝑥 〗 = lim┬(x→0) (1 −〖 cos〗𝑥)/sin〖𝑥 〗 × (𝟏 + 𝐜𝐨𝐬𝒙)/(𝟏 + 𝒄𝒐𝒔𝒙 ) = lim┬(x→0) (1^2 −〖 cos^2〗𝑥)/(sin〖𝑥 〗 (1 + cos𝑥 ) ) = lim┬(x→0) (𝟏 −〖 〖𝒄𝒐𝒔〗^𝟐〗𝒙)/(sin〖𝑥 〗 (1 + cos𝑥 ) ) = lim┬(x→0) 〖 〖𝐬𝐢𝐧〗^𝟐〗𝒙/(sin〖𝑥 〗 (1 + cos𝑥 ) ) = lim┬(x→0) 〖 𝑠𝑖𝑛〗𝑥/((1 + cos𝑥 ) ) Putting x = 0 = 〖 𝑠𝑖𝑛〗0/((1 + cos0 ) ) = 0/(1 + 1) = 0/2 = 0 Ex 12.1, 21 (Method 2) Evaluate the Given limit: lim┬(x→0) (cosec x – cot x) (𝑙𝑖𝑚)┬(𝑥→0) (cosec x – cot x) = (𝑙𝑖𝑚)┬(𝑥→0) ((𝑐𝑜𝑠𝑒𝑐 𝑥 − 𝑐𝑜𝑡〖𝑥) 〗)/𝟏 = (𝑙𝑖𝑚)┬(𝑥→0) (𝑐𝑜𝑠𝑒𝑐 𝑥 −〖 𝑐𝑜𝑡〗𝑥)/(𝒄𝒐𝒔𝒆𝒄𝟐 𝒙 − 𝒄𝒐𝒕𝟐 𝒙) = (𝑙𝑖𝑚)┬(𝑥→0) (𝑐𝑜𝑠𝑒𝑐 𝑥 −〖 𝑐𝑜𝑡〗𝑥)/((𝑐𝑜𝑠𝑒𝑐 𝑥 −〖 𝑐𝑜𝑡〗〖𝑥) (𝑐𝑜𝑠𝑒𝑐 𝑥 +〖 𝑐𝑜𝑡〗〖𝑥)〗 〗 ) = (𝑙𝑖𝑚)┬(𝑥→0) 1/(𝑐𝑜𝑠𝑒𝑐 𝑥 +〖 𝑐𝑜𝑡〗𝑥 ) (𝑈𝑠𝑖𝑛𝑔 𝑐𝑜𝑠𝑒𝑐2 𝜃−𝑐𝑜𝑡2 𝜃=1) Using cosec θ = (1 )/(sin θ) cot θ = (cos θ)/(sin θ) = (𝑙𝑖𝑚)┬(𝑥→0) 1/(1/𝑠𝑖𝑛𝑥 + 𝑐𝑜𝑠𝑥/𝑠𝑖𝑛𝑥 ) = (𝑙𝑖𝑚)┬(𝑥→0) 1/((1 + 〖 𝑐𝑜𝑠〗𝑥)/𝑠𝑖𝑛𝑥 ) = (𝑙𝑖𝑚)┬(𝑥→0) 𝑠𝑖𝑛𝑥/(1 + 𝑐𝑜𝑠𝑥 ) Putting x = 0 = sin0/(1 +〖 cos〗0 ) = 0/(1 + 1) = 0/2 = 0 Ex 12.1, 21 (Method 3) Evaluate the Given limit: lim┬(x→0) (cosec x – cot x) (𝑙𝑖𝑚)┬(𝑥→0) (cosec 𝑥 − cot 𝑥) = (𝑙𝑖𝑚)┬(𝑥→0) 1/sin𝑥 − cos𝑥/sin𝑥 = (𝑙𝑖𝑚)┬(𝑥→0) ((1 − cos𝑥)/sin𝑥 ) Using 1 − cos 2𝜃 = 2 sin2 𝜃 and sin 2𝜃 = 2 sin 𝜃 cos 𝜃 = (𝑙𝑖𝑚)┬(𝑥→0) (2 sin^2〖 𝑥/2〗)/(2 sin〖 𝑥/2〗 cos〖 𝑥/2〗 ) = (𝑙𝑖𝑚)┬(𝑥→0) tan〖𝑥/2〗 Putting x = 0 = tan 0 = 0