Ex 12.2, 3 - Chapter 12 Class 11 Limits and Derivatives

Last updated at Dec. 16, 2024 by

Slide4.JPG

Slide5.JPG

Go Ad-free

Transcript

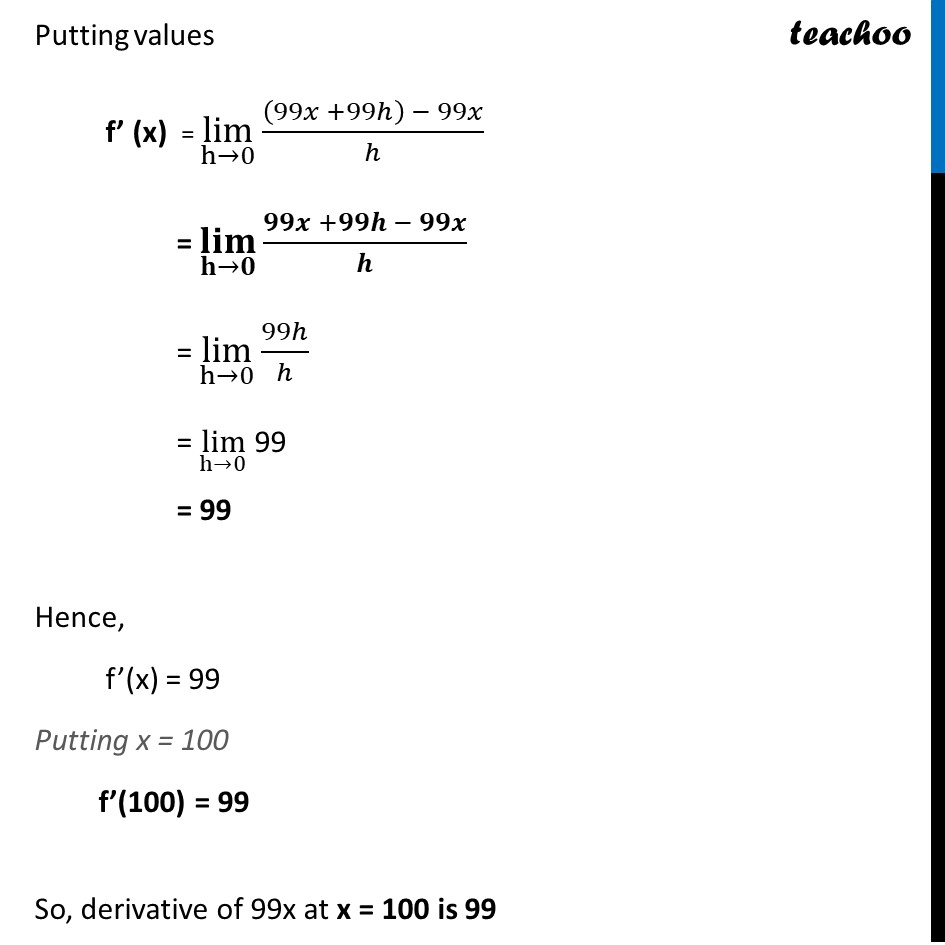
Ex 12.2, 3 Find the derivative of 99x at x = 100 Let f (x) = x We need to find derivative of f(x) at x = 100 i.e. f’ (100) We know that f’ (x) = (π‘™π‘–π‘š)┬(β„Žβ†’0)⁑〖(𝑓(π‘₯ + β„Ž) βˆ’ 𝑓 (π‘₯))/β„Žγ€— Here, f(x) = 99x So, f(x + h) = 99(x + h) = 99x + 99h Putting values f’ (x) = lim┬(hβ†’0)⁑〖((99π‘₯ +99β„Ž) βˆ’ 99π‘₯)/β„Žγ€— = lim┬(hβ†’0)⁑〖(99π‘₯ +99β„Ž βˆ’ 99π‘₯)/β„Žγ€— = lim┬(hβ†’0)⁑〖99β„Ž/β„Žγ€— = lim┬(hβ†’0) 99 = 99 Hence, f’(x) = 99 Putting x = 100 f’(100) = 99 So, derivative of 99x at x = 100 is 99

Davneet Singh's photo - Co-founder, Teachoo

Made by

Davneet Singh

Davneet Singh has done his B.Tech from Indian Institute of Technology, Kanpur. He has been teaching from the past 14 years. He provides courses for Maths, Science and Computer Science at Teachoo