
Last updated at Dec. 16, 2024 by Teachoo




Transcript
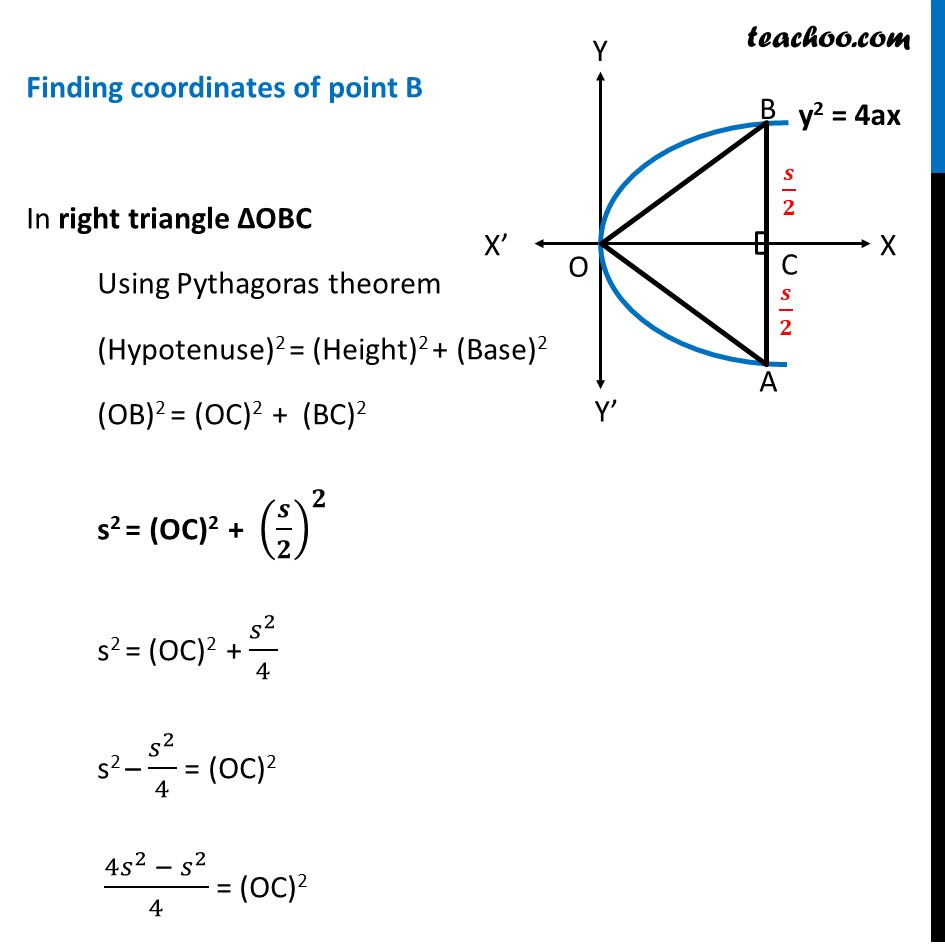
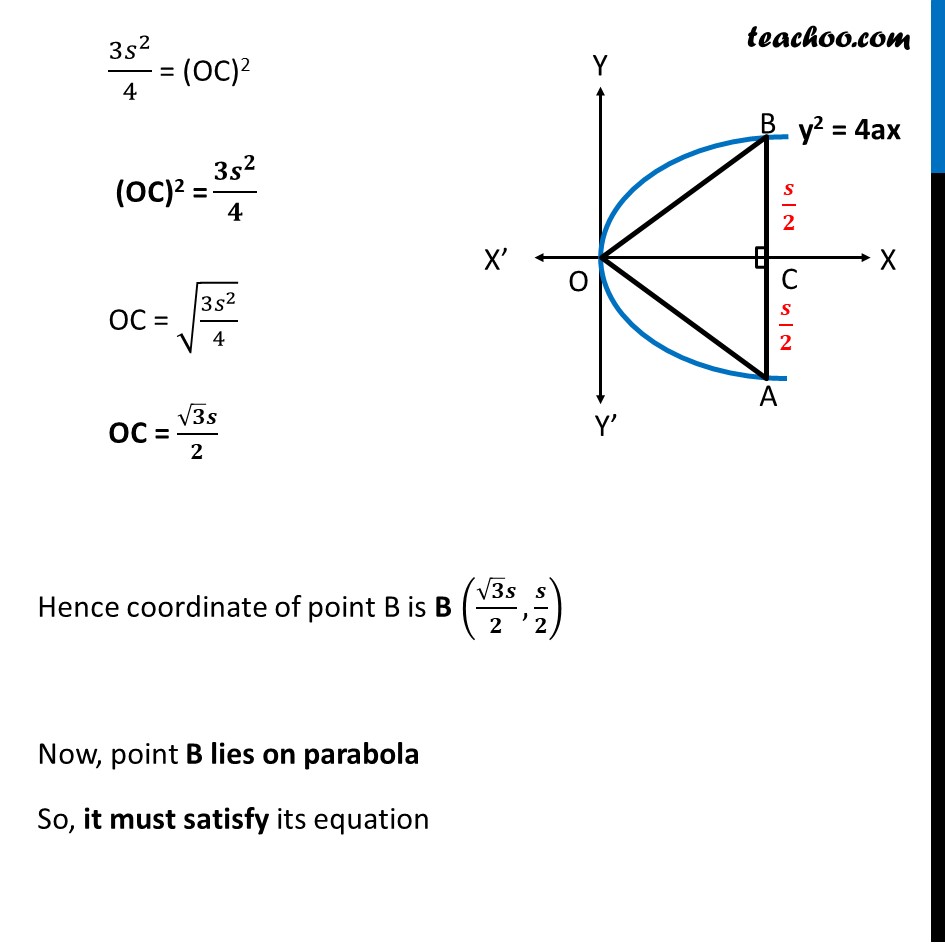
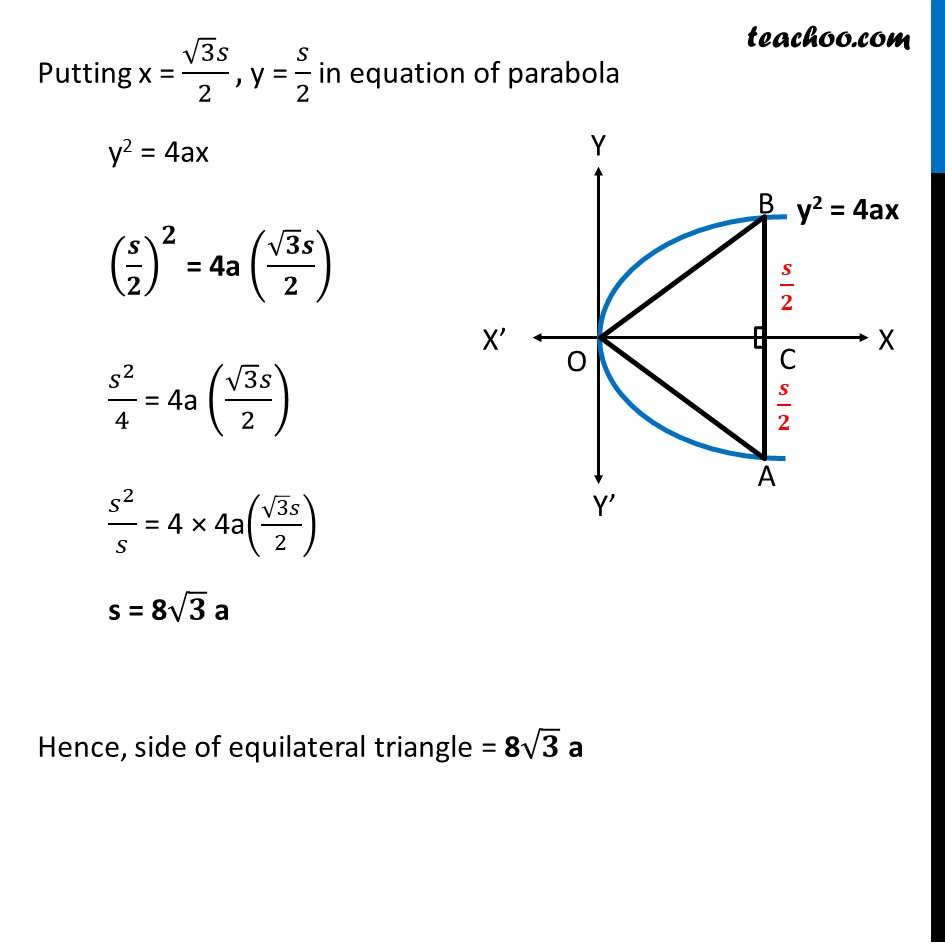
Misc 8 An equilateral triangle is inscribed in the parabola y2 = 4ax, where one vertex is at the vertex of the parabola. Find the length of the side of the triangle. Let length of equilateral triangle be s Hence OA = OB = AB = s Here, OC AB So, OCA = OCB = 90 And AC = BC So, AC = BC = 2 AC = BC = 2 We find coordinates of point B Now, in right triangle OBC Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 (OB)2 = (OC)2 + (BC)2 s2 = (OC)2 + 2 2 s2 = (OC)2 + 2 4 s2 2 4 = (OC)2 4 2 2 4 = (OC)2 3 2 4 = (OC)2 (OC)2 = 3 2 4 OC = 3 2 4 OC = 3 2 Hence coordinate of point B is B( , ) Now, point B lies on parabola So, it must satisfy its equation Putting x = 3 2 , y = 2 in equation of parabola y2 = 4ax 2 2 = 4a( 3 2 ) 2 4 = 4a( 3 2 ) 2 = 4 4a( 3 2 ) s = 8 a Hence, side of equilateral triangle = 8 3 a