Misc, 5 - Chapter 10 Class 11 Conic Sections

Transcript

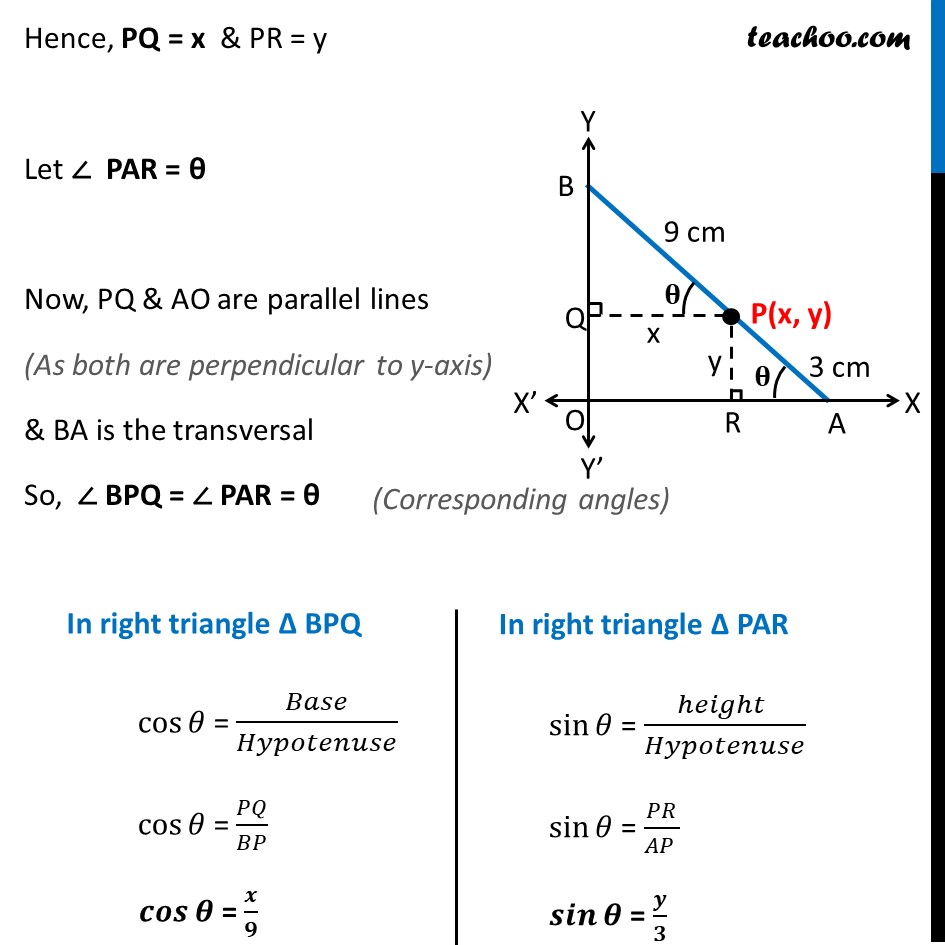
Misc, 5 A rod of length 12 cm moves with its ends always touching the coordinate axes. Determine the equation of the locus of a point P on the rod, which is 3 cm from the end in contact with the x-axis. Let AB be the rod where A touches the x-axis & B touches the y-axis Let point P(x, y) Given AB = Length of rod = 12 cm & AP = 3 cm PB = AB – AP PB = 12 – 3 = 9cm Drawing PQ ⊥ BO and PR ⊥ OA Hence, PQ = x & PR = y Let ∠ PAR = θ Now, PQ & AO are parallel lines (As both are perpendicular to y-axis) & BA is the transversal So ∠ BPQ = ∠ PAR = θ Now we know that, ﷐ sin2﷮𝜃﷯ + ﷐cos2﷮𝜃﷯ = 1 Putting ﷐ 𝑠𝑖𝑛﷮𝜃﷯ = ﷐𝑦﷮6﷯ and ﷐𝑐𝑜𝑠﷮𝜃﷯ = ﷐𝑥﷮9﷯ ﷐﷐﷐𝑦﷮3﷯﷯﷮2﷯ + ﷐﷐﷐𝑥﷮9﷯﷯﷮2﷯ = 1 ﷐𝑦2﷮9﷯ + ﷐𝑥2﷮81﷯ = 1 ﷐𝒙𝟐﷮𝟖𝟏﷯ + ﷐𝒚𝟐﷮𝟗﷯ = 1 Hence it satisfies the equation of ellipse ﷐﷐𝑥﷮2﷯﷮﷐𝑎﷮2﷯﷯ + ﷐﷐𝑦﷮2﷯﷮﷐𝑏﷮2﷯﷯ = 1 Thus locus of P is ellipse