Question 16 - Figure it out - Page 185 to 189 - Chapter 7 Class 7 - Finding the Unknown (Ganita Prakash II)

Transcript

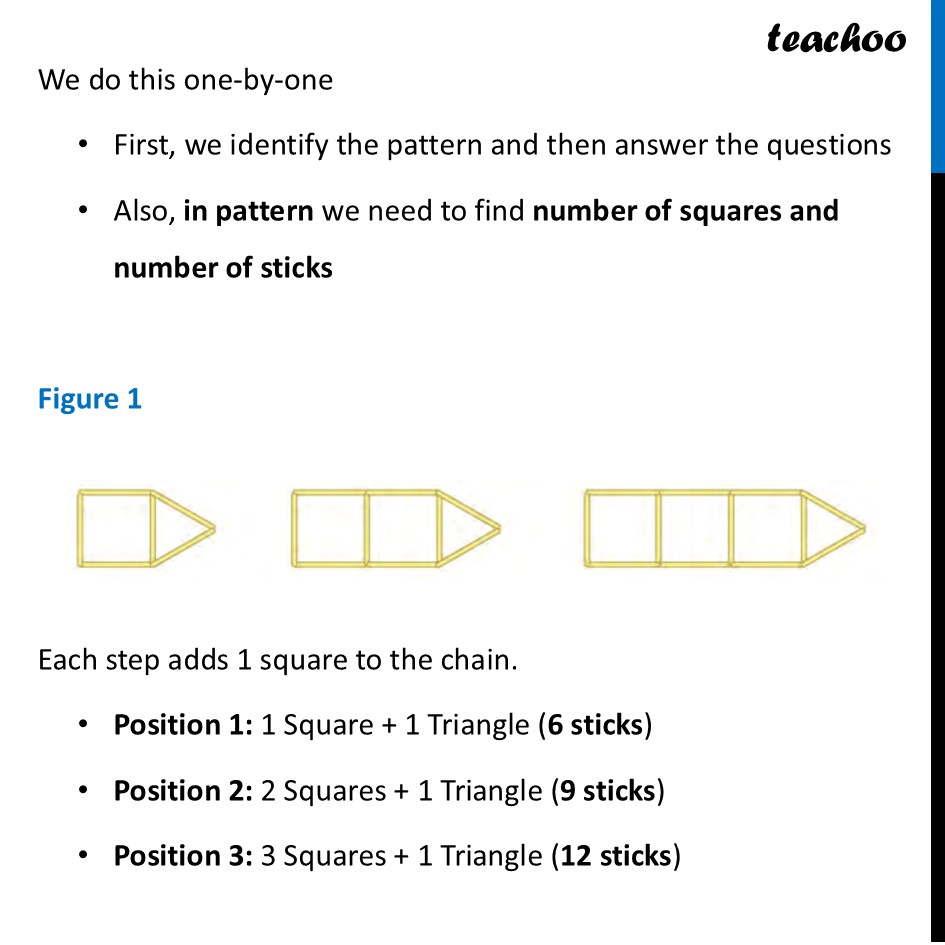
Question 16 Two separate figures are given below. Each figure shows the first few positions in a sequence of arrangements made with sticks. Identify the pattern and answer the following questions for each figure: (a) How many squares are in position number 11 of the sequence? (b) How many sticks are needed to make the arrangement in position number 11 of the sequence? (c) Can an arrangement in this sequence be made using exactly 85 sticks? If yes, which position number will it correspond to? (d) Can an arrangement in this sequence be made using exactly 150 sticks? If yes, which position number will it correspond to?We do this one-by-one First, we identify the pattern and then answer the questions Also, in pattern we need to find number of squares and number of sticks Figure 1 Each step adds 1 square to the chain. Position 1: 1 Square + 1 Triangle (6 sticks) Position 2: 2 Squares + 1 Triangle (9 sticks) Position 3: 3 Squares + 1 Triangle (12 sticks) Thus, we can say Number of Squares = 𝒏 And, Number of Sticks =𝟑𝒏+𝟑 Where n = Number of Steps Let’s answer our questiojns How many squares are in position number 11 of the sequence? For n = 11 Number of Square = n = 11 (b) How many sticks are needed to make the arrangement in position number 11 of the sequence? For n = 11 Number of Sticks = 3n + 3 = 3 × 11 + 3 = 33 + 3 = 36 Since position number equals the number of squares: 𝟏𝟏 squares. (c) Can an arrangement in this sequence be made using exactly 85 sticks? If yes, which position number will it correspond to? We put Number of sticks = 85 And find n So, our equation becomes 3n + 3 = 85 Putting 3 on right side, it becomes – 3 3n = 85 – 3 3n = 82 Putting 3 on right side, it becomes division n = 82/3 n = 27.33… Since n is in decimal, it is not possible Thus, the arrangement is not possible (d) Can an arrangement in this sequence be made using exactly 150 sticks? If yes, which position number will it correspond to? We put Number of sticks = 150 And find n So, our equation becomes 3n + 3 = 150 Putting 3 on right side, it becomes – 3 3n = 150 – 3 3n = 147 Putting 3 on right side, it becomes division n = 147/3 n = 49 Thus, the arrangement is possible and position number is 49 Figure 2 Each step adds a "step" of 3 squares. Position 1: 4 squares (13 sticks) Position 2: 4 Squares + 3 Squares (13 + 9 = 22 sticks) Position 3: 7 Squares + 3 Squares (22 + 9 = 32 sticks) Thus, we can say Number of Squares = 𝟒+𝟑 × (𝒏−𝟏) And, Number of Sticks =𝟏𝟑+𝟗 × (𝒏−𝟏) Where n = Number of Steps Let’s answer our questiojns How many squares are in position number 11 of the sequence? For n = 11 Number of Square = 4 + 3 × (n – 1) = 4 + 3 × (11 – 1) = 4 + 3 × 10 = 4 + 30 = 34 (b) How many sticks are needed to make the arrangement in position number 11 of the sequence? For n = 11 Number of Sticks = 13 + 9 × (n – 1) = 13 + 9 × (11 – 1) = 13 + 9 × 10 = 13 + 90 = 103 Since position number equals the number of squares: 𝟏𝟏 squares. (c) Can an arrangement in this sequence be made using exactly 85 sticks? If yes, which position number will it correspond to? We put Number of sticks = 85 And find n So, our equation becomes 13 + 9 × (n – 1) = 85 13 + 9n – 9 = 85 9n + (13 – 9) = 85 9n + 4 = 85 Putting 4 on right side, it becomes –4 9n = 85 – 4 9n = 81 Putting 9 on right side, it becomes division n = 81/9 n = 9 Thus, the arrangement is possible and position number is 49 (d) Can an arrangement in this sequence be made using exactly 150 sticks? If yes, which position number will it correspond to? We put Number of sticks = 150 And find n So, our equation becomes 13 + 9 × (n – 1) = 150 13 + 9n – 9 = 150 9n + (13 – 9) = 150 9n + 4 = 150 Putting 4 on right side, it becomes –4 9n = 150 – 4 9n = 146 Putting 9 on right side, it becomes division n = 146/9 n = 16.22… Since n is in decimal, it is not possible Thus, the arrangement is not possible