![[Class 7] Draw a line l and mark a point P anywhere outside the line - Figure it out - Pag 154, 155](https://cdn.teachoo.com/60cf6631-0daf-4fc7-8480-2f8fd3a9b98b/slide260.jpg)

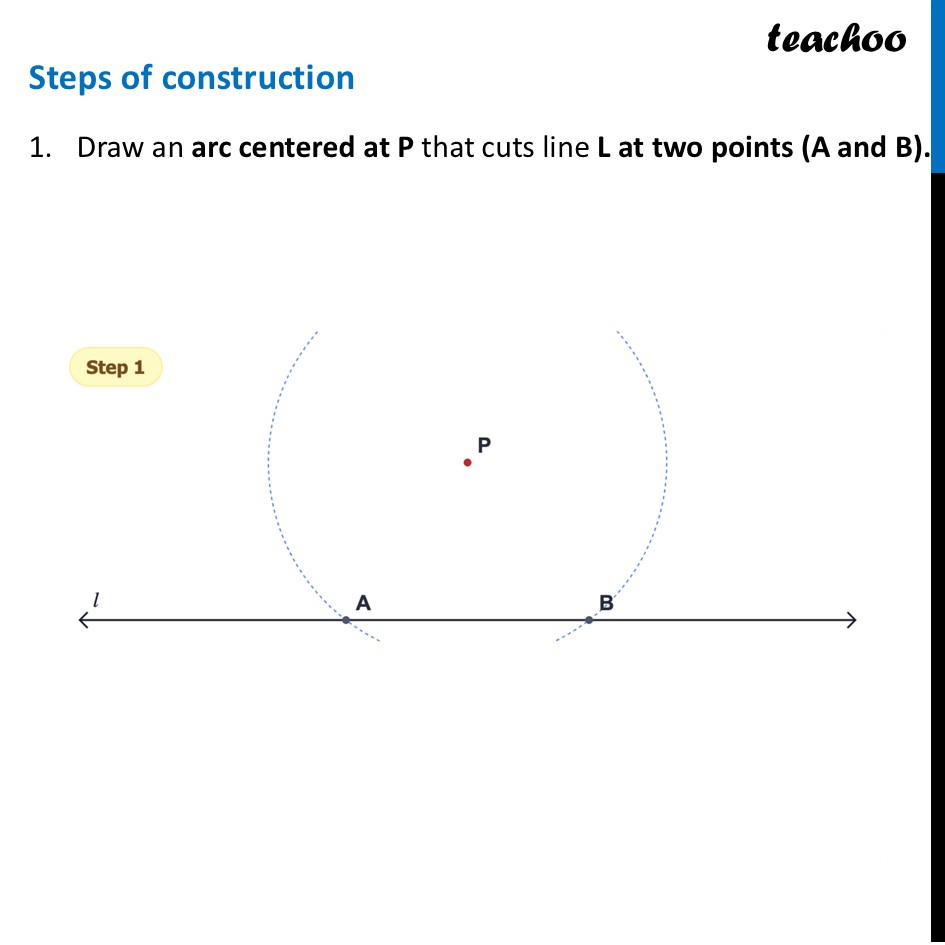
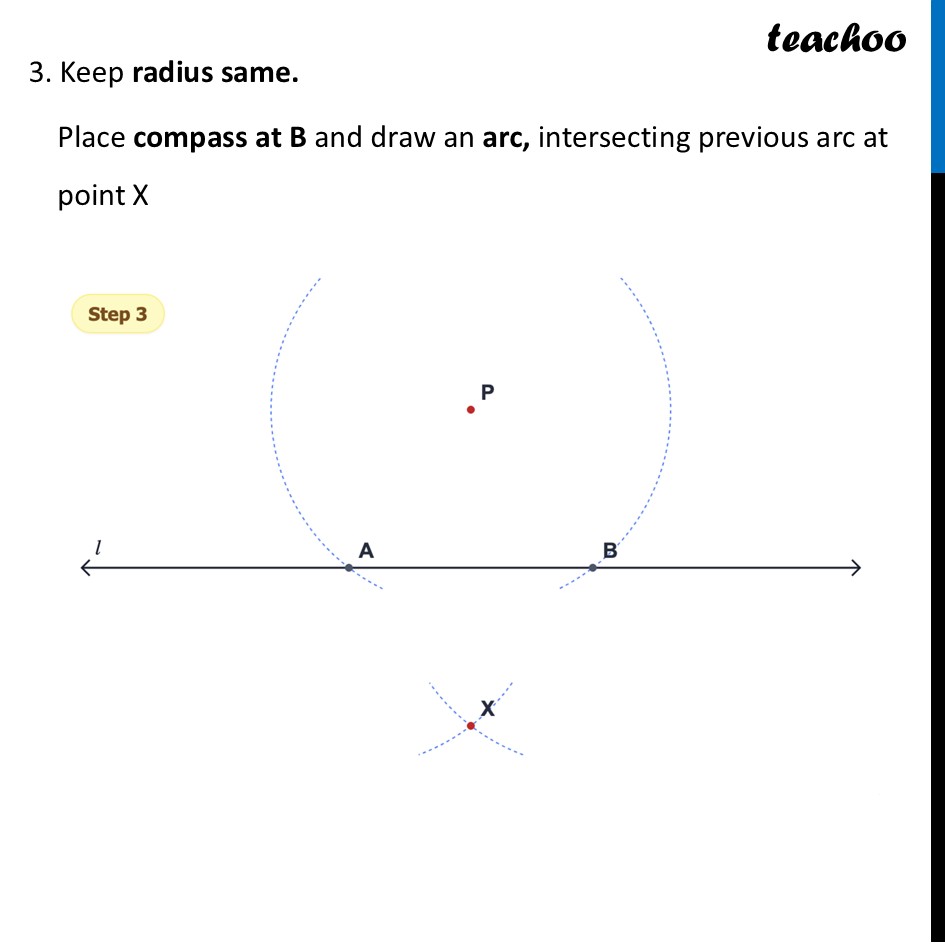
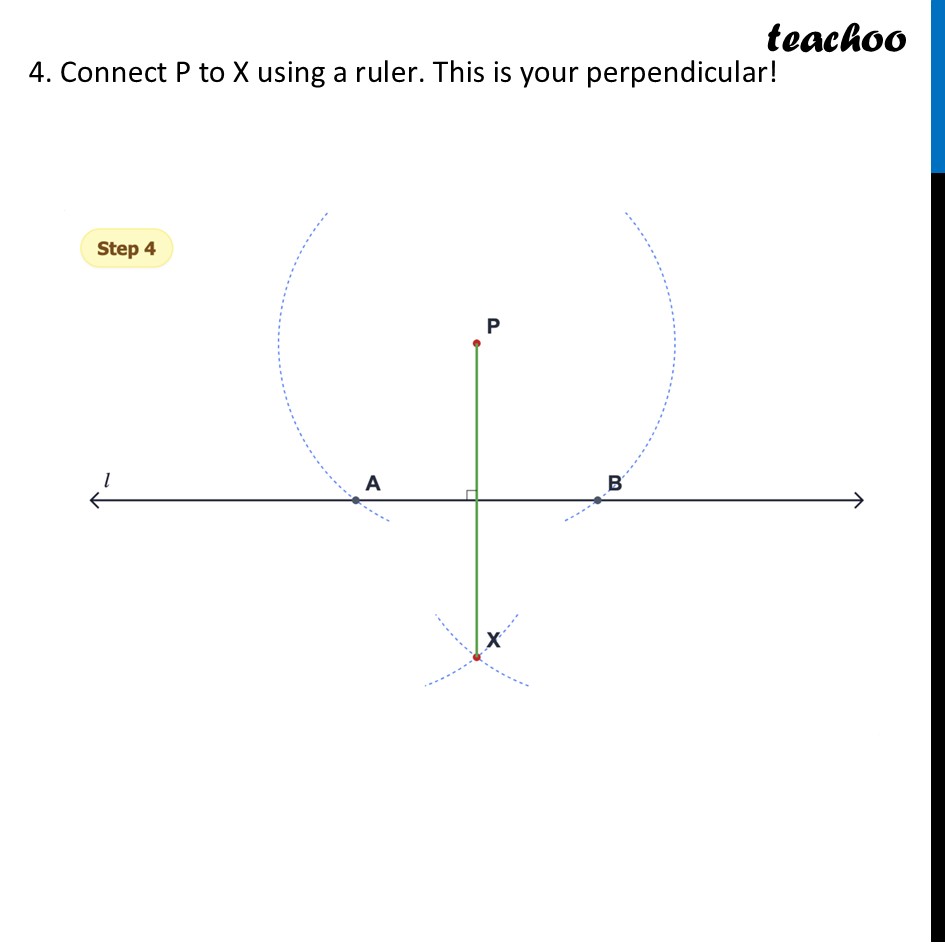

Figure it out - Pag 154, 155
Last updated at February 6, 2026 by Teachoo
![[Class 7] Draw a line l and mark a point P anywhere outside the line - Figure it out - Pag 154, 155](https://cdn.teachoo.com/60cf6631-0daf-4fc7-8480-2f8fd3a9b98b/slide260.jpg)





Transcript
Question 4 Draw a line l and mark a point P anywhere outside the line. Construct a perpendicular to the given line l through P. [Hint: Find a line segment on l whose perpendicular bisector passes through P.]Our figure looks like this To make the perpendicular through point P, we make 90° angle which passes through point P That is only possible if point P lies on perpendicular bisector a line segment, and the line segment is on line l We follow these steps Make a line segment on line l from point P (by making equal arcs) Drawing perpendicular bisector of line segment (below the line) by keeping radius same Joining perpendicular bisector below and point P Steps of construction Draw an arc centered at P that cuts line L at two points (A and B). 3. Keep radius same. Place compass at B and draw an arc, intersecting previous arc at point X 4. Connect P to X using a ruler. This is your perpendicular! Why is this a perpendicular bisector? This construction works because of the Properties of a Rhombus (or Kite): Point P is equidistant: When you drew the first big arc, you made sure the distance from 𝐏 to 𝐀 was exactly the same as the distance from 𝐏 to 𝐁. This puts 𝐏 on the perpendicular bisector of the segment AB . Point 𝐗 is equidistant: When you drew the arcs from 𝐴 and 𝐵 with the same radius, you ensured the distance from 𝐗 to 𝐀 was the same as the distance from 𝐗 to B. This puts 𝐗 on the perpendicular bisector of 𝐴𝐵 as well. Two points determine a line: Since both P and X are on the perpendicular bisector, the line connecting them must be the perpendicular bisector!