You are here
Constructing 6-Pointed Star
Last updated at February 6, 2026 by Teachoo
Constructing Regular Hexagon, Angle 60° and 6-pointed Star
Class 7 (Ganita Prakash 1, 2 & old NCERT)
Chapter 6 Class 7 - Constructions and Tilings (Ganita Prakash II)
- Constructing an Eye
- Constructing a Perpendicular Bisector
- Constructing angle 90°
- Construction Methods in Śulba-Sūtras
- Constructing Angle Bisectors
- Figure it out - Pag 144, 145
- Constructing Copy of an Angle
- Construction of a Line Parallel to the Given Line
- Constructing Arch Designs
-
Constructing Regular Hexagon, Angle 60° and 6-pointed Star
- Figure it out - Pag 154, 155
- Tangrams
- Tiling
- Figure it out - Page 160
- Tiling the Entire Plane
Transcript
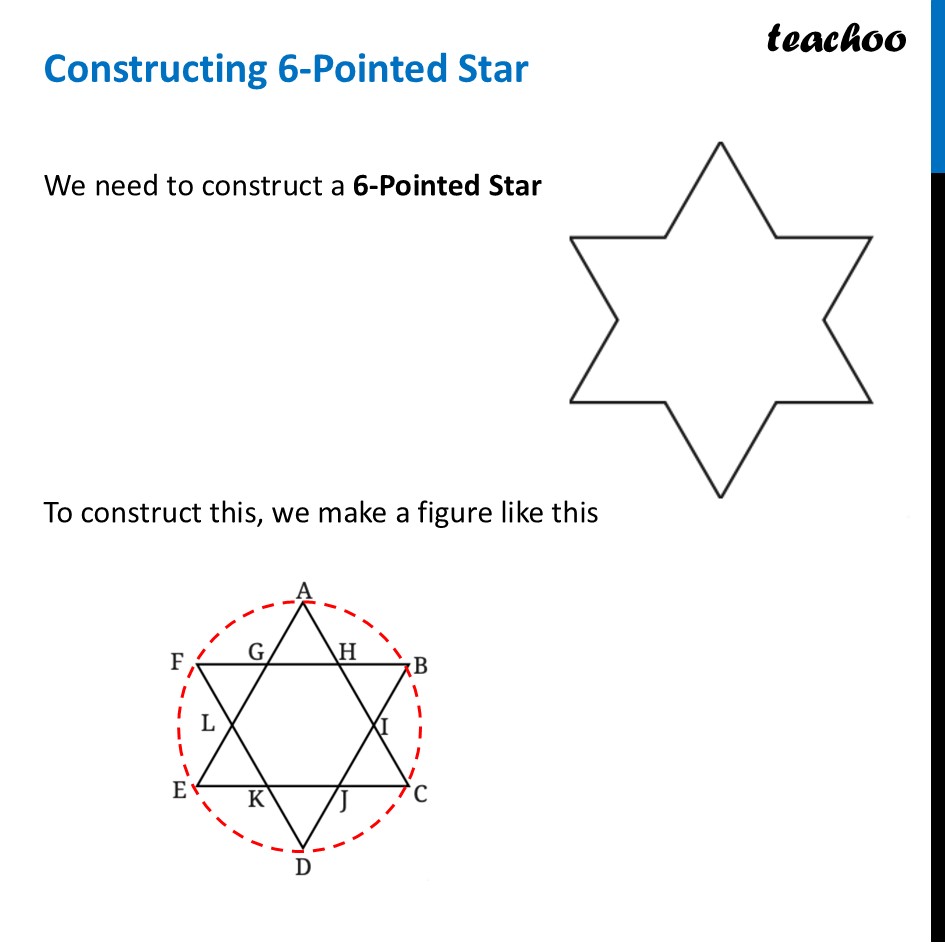
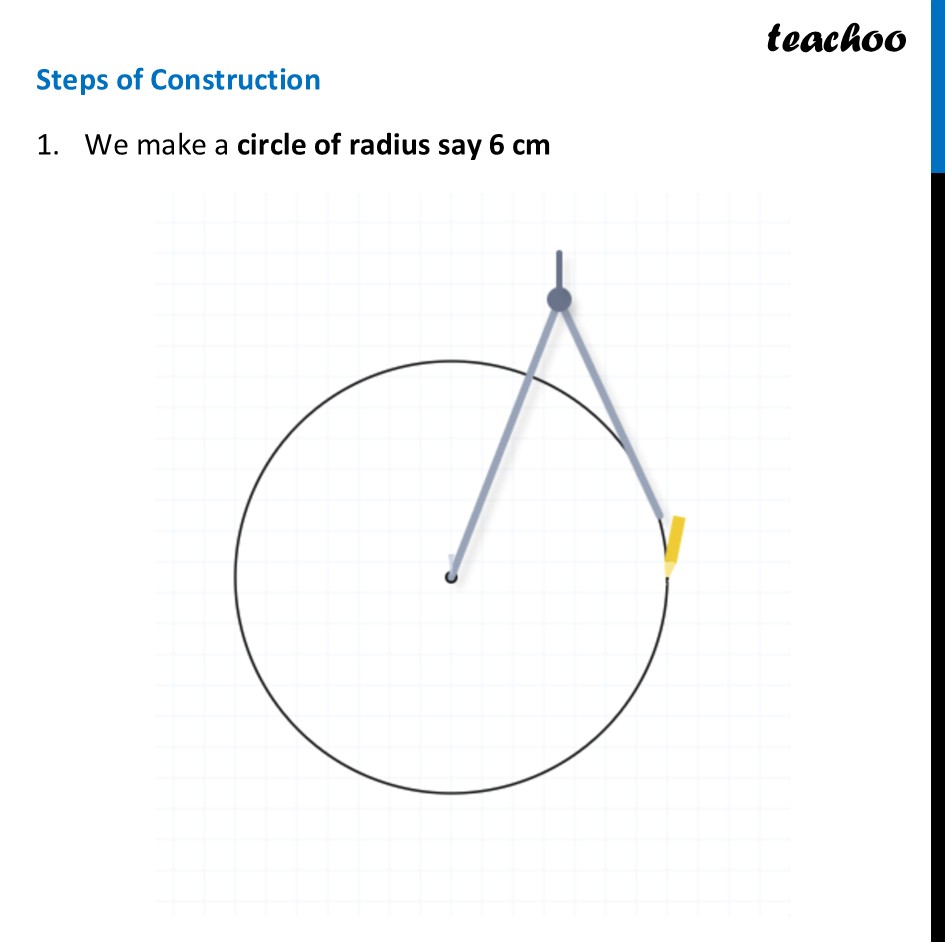
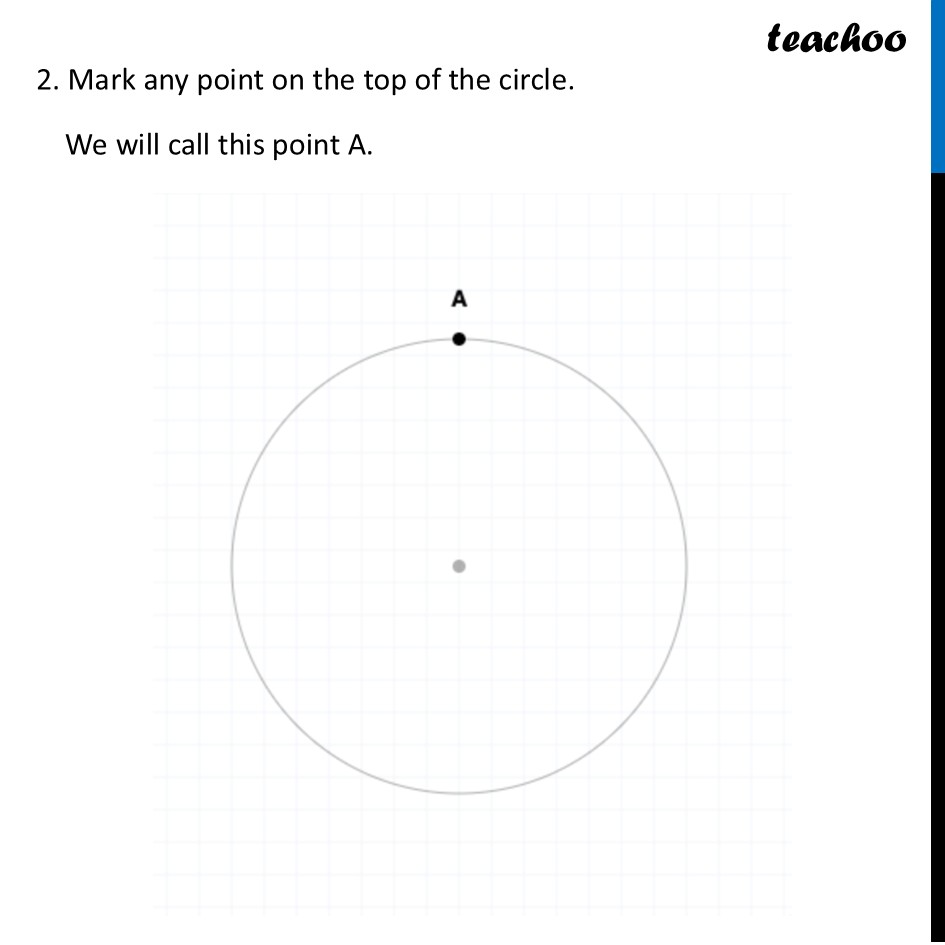
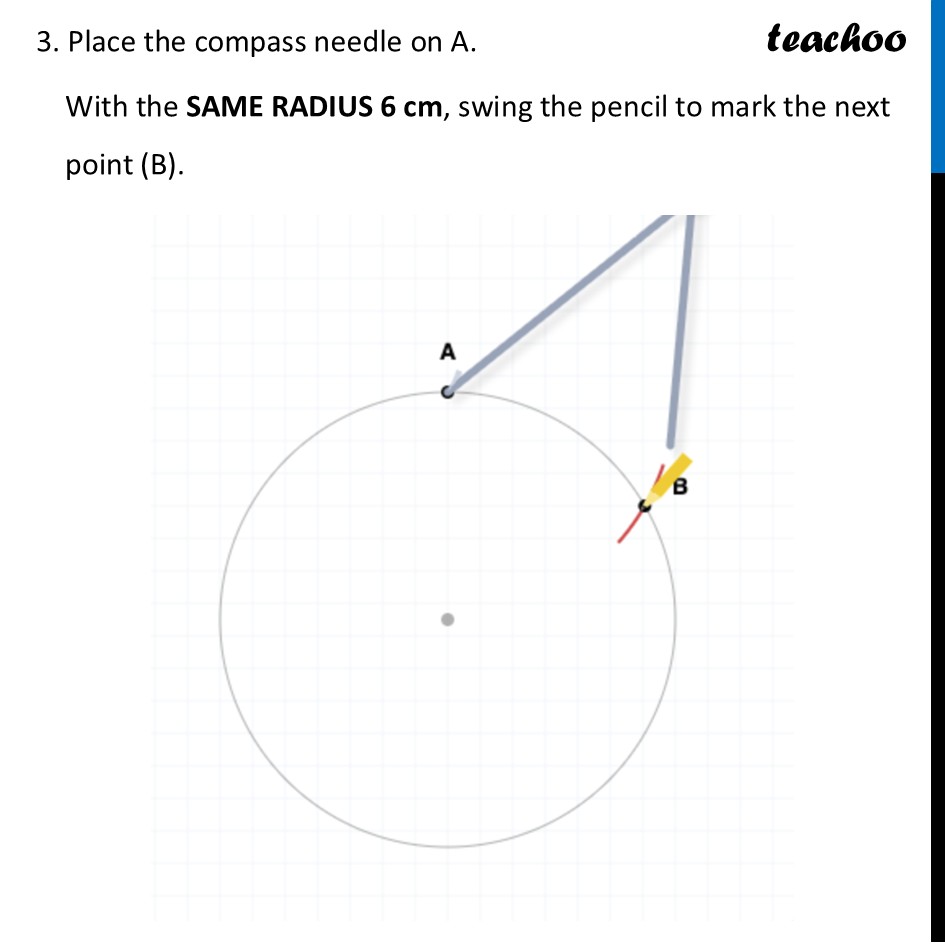
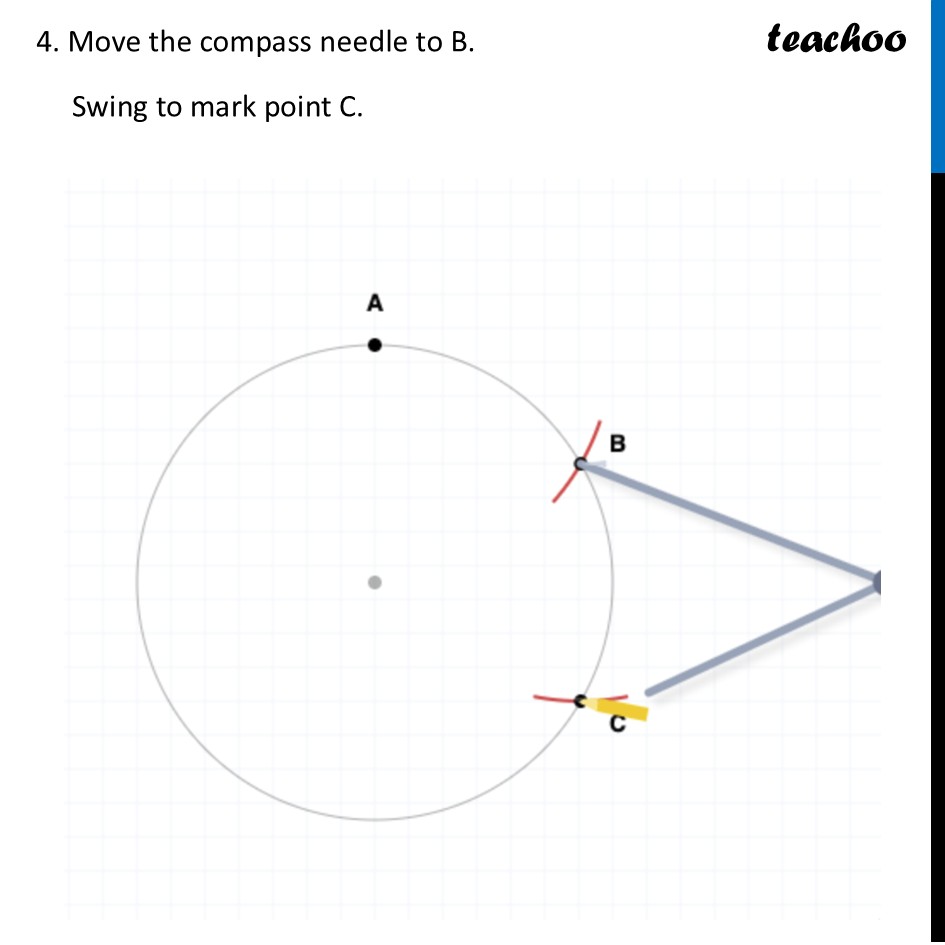
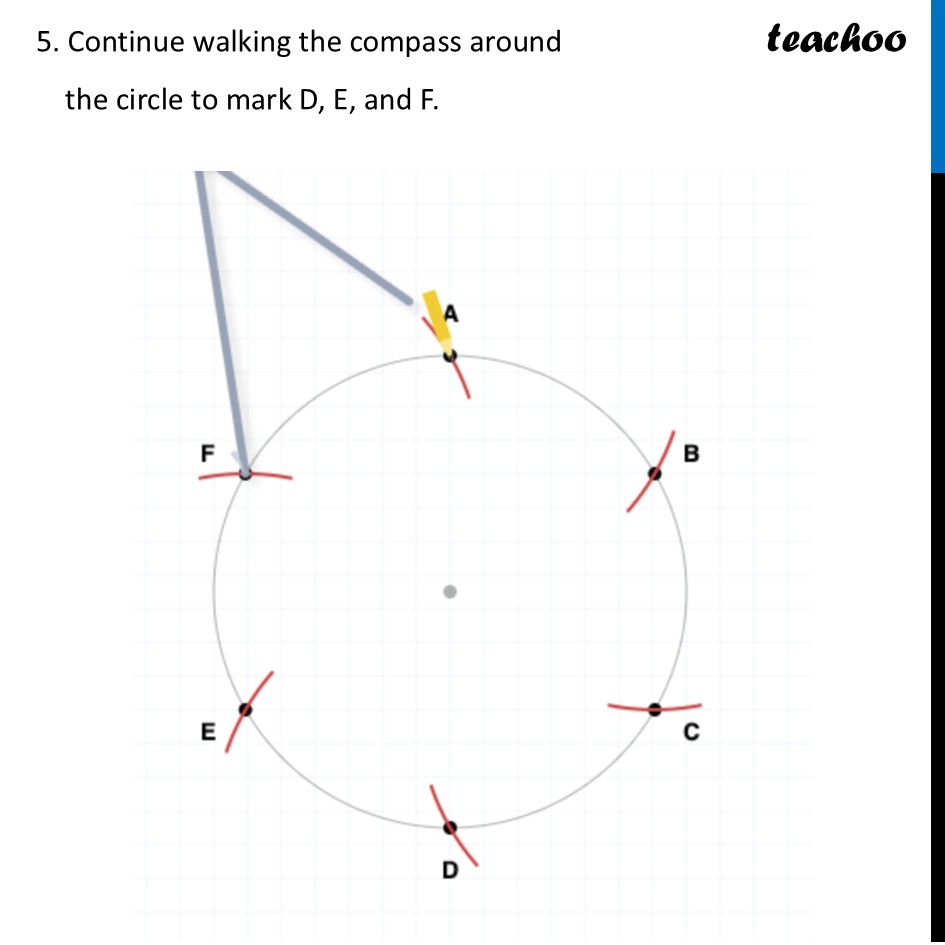
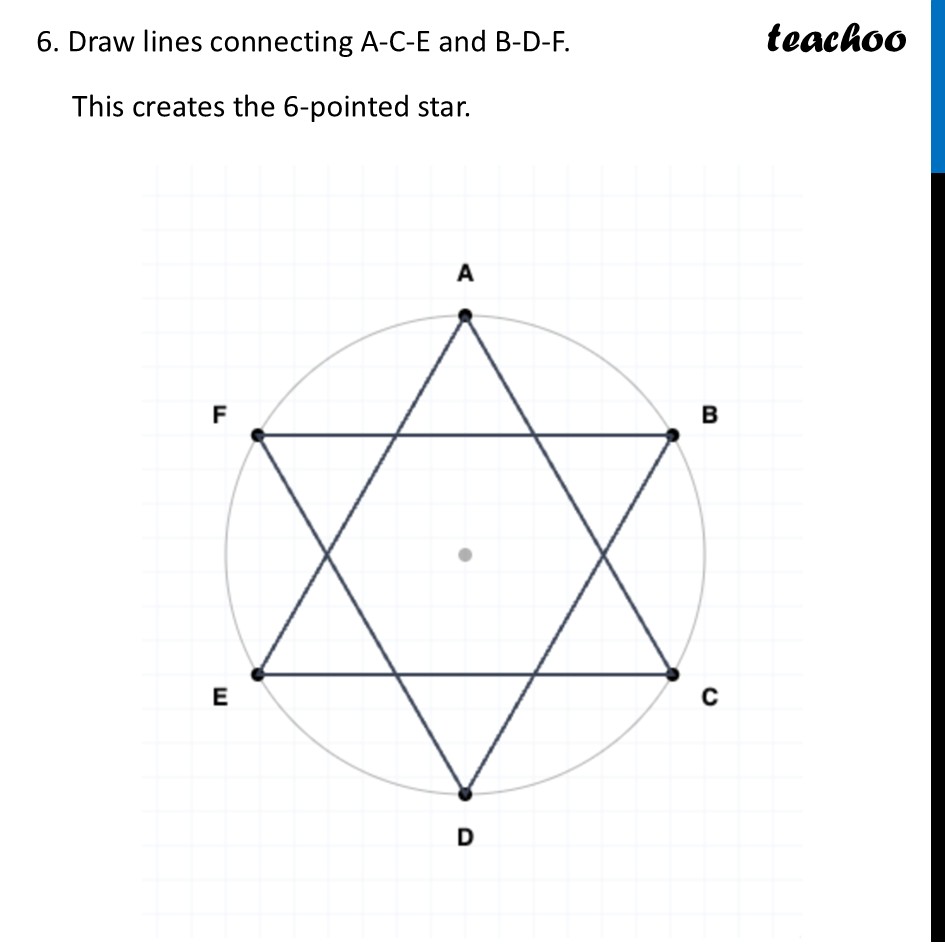
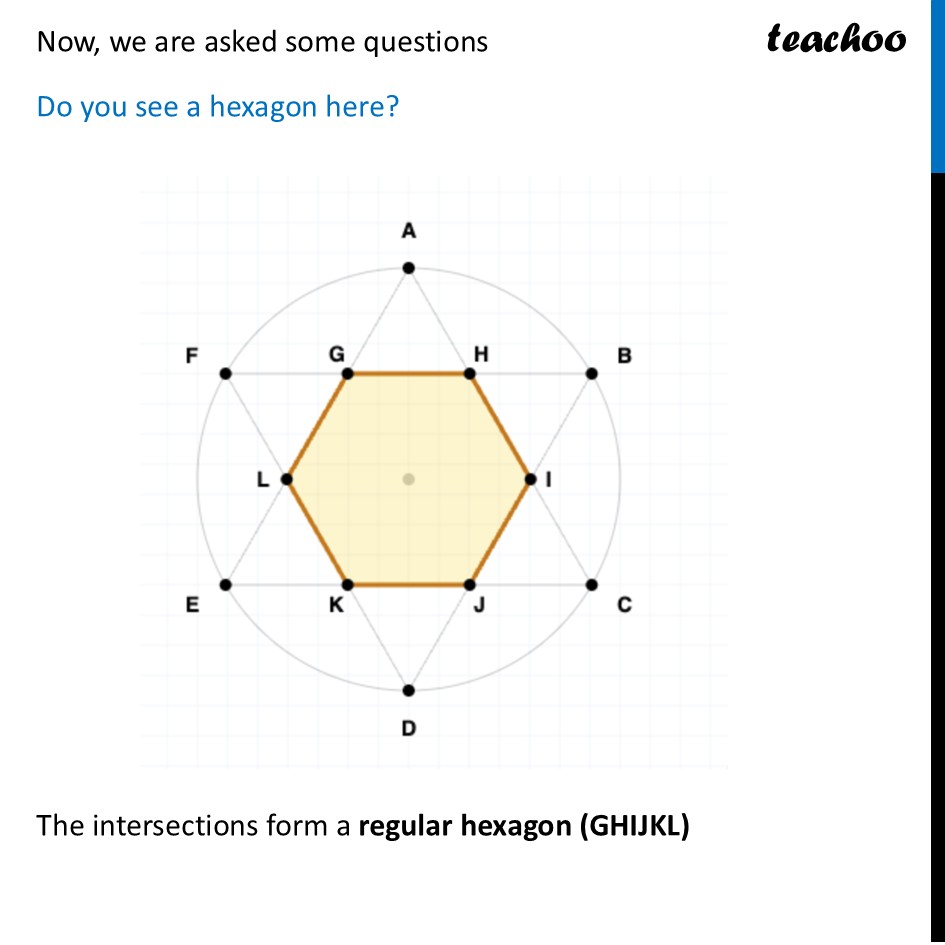
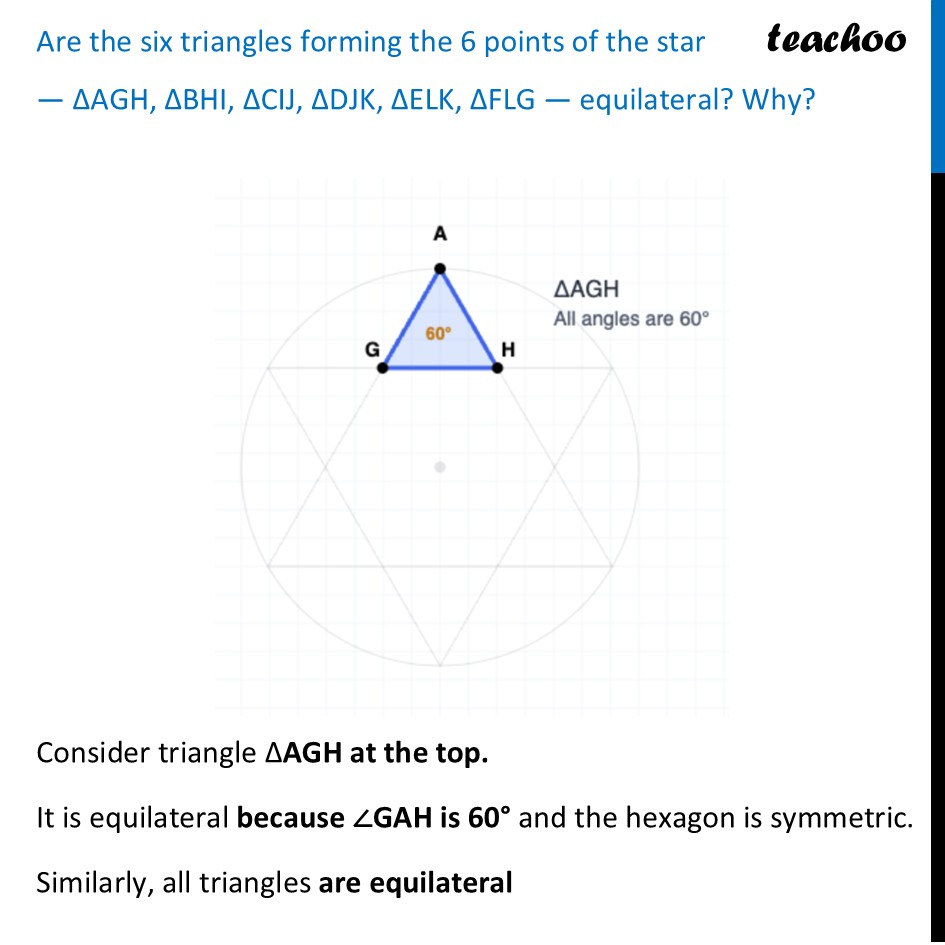
Constructing 6-Pointed StarWe need to construct a 6-Pointed Star To construct this, we make a figure like this Steps of Construction We make a circle of radius say 6 cm 2. Mark any point on the top of the circle. We will call this point A. 3. Place the compass needle on A. With the SAME RADIUS 6 cm, swing the pencil to mark the next point (B). 4. Move the compass needle to B. Swing to mark point C. 5. Continue walking the compass around the circle to mark D, E, and F. 6. Draw lines connecting A-C-E and B-D-F. This creates the 6-pointed star. Now, we are asked some questions Do you see a hexagon here? The intersections form a regular hexagon (GHIJKL) Are the six triangles forming the 6 points of the star — ∆AGH, ∆BHI, ∆CIJ, ∆DJK, ∆ELK, ∆FLG — equilateral? Why? Consider triangle ΔAGH at the top. It is equilateral because ∠GAH is 60° and the hexagon is symmetric. Similarly, all triangles are equilateral
