Question 3 - Figure it out - Pag 144, 145 - Chapter 6 Class 7 - Constructions and Tilings (Ganita Prakash II)

Transcript

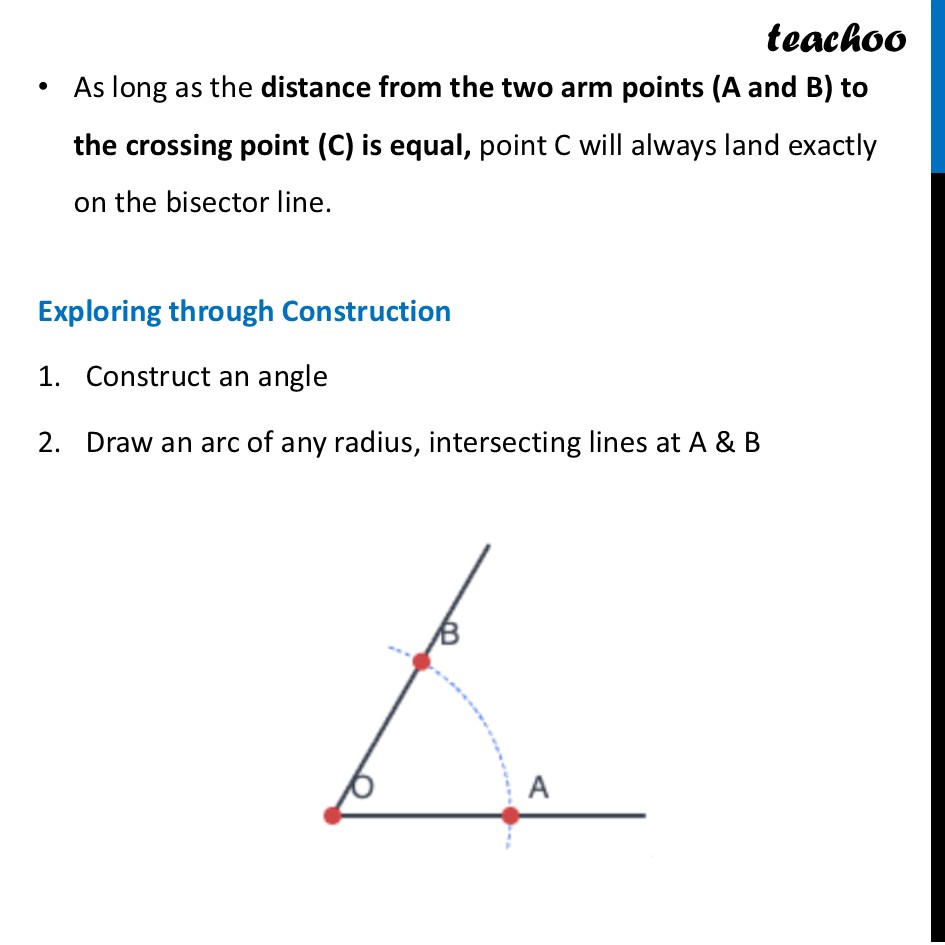
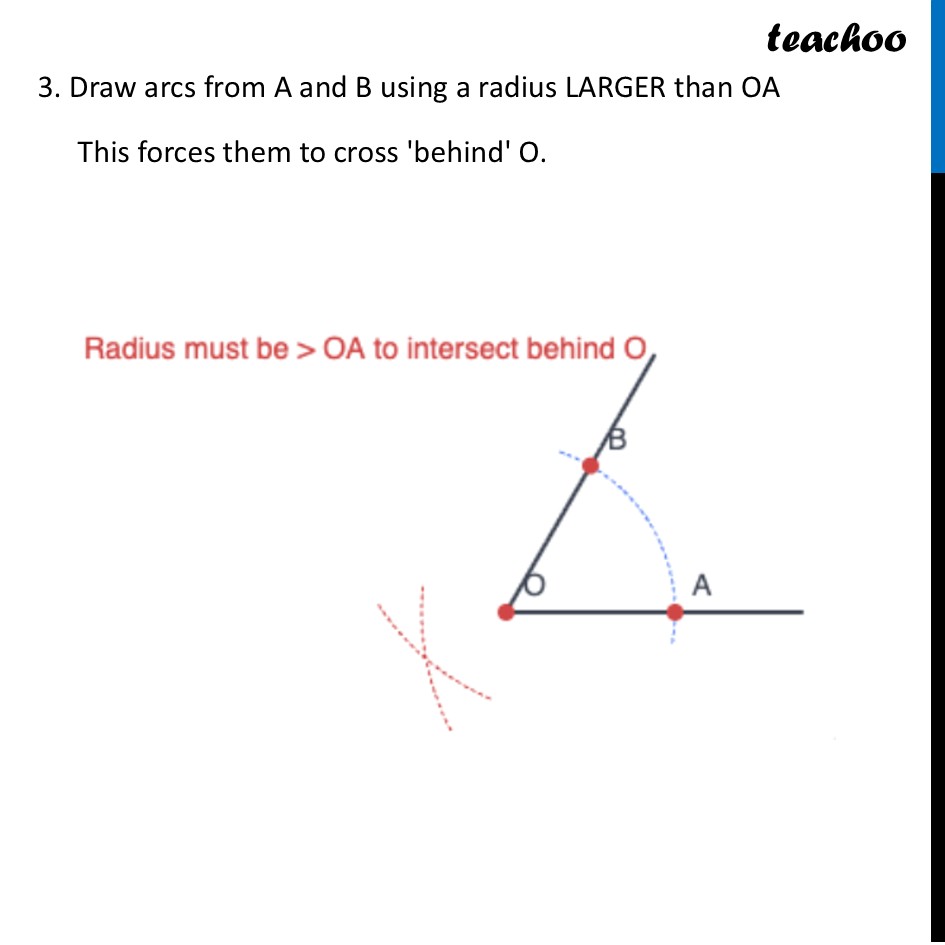
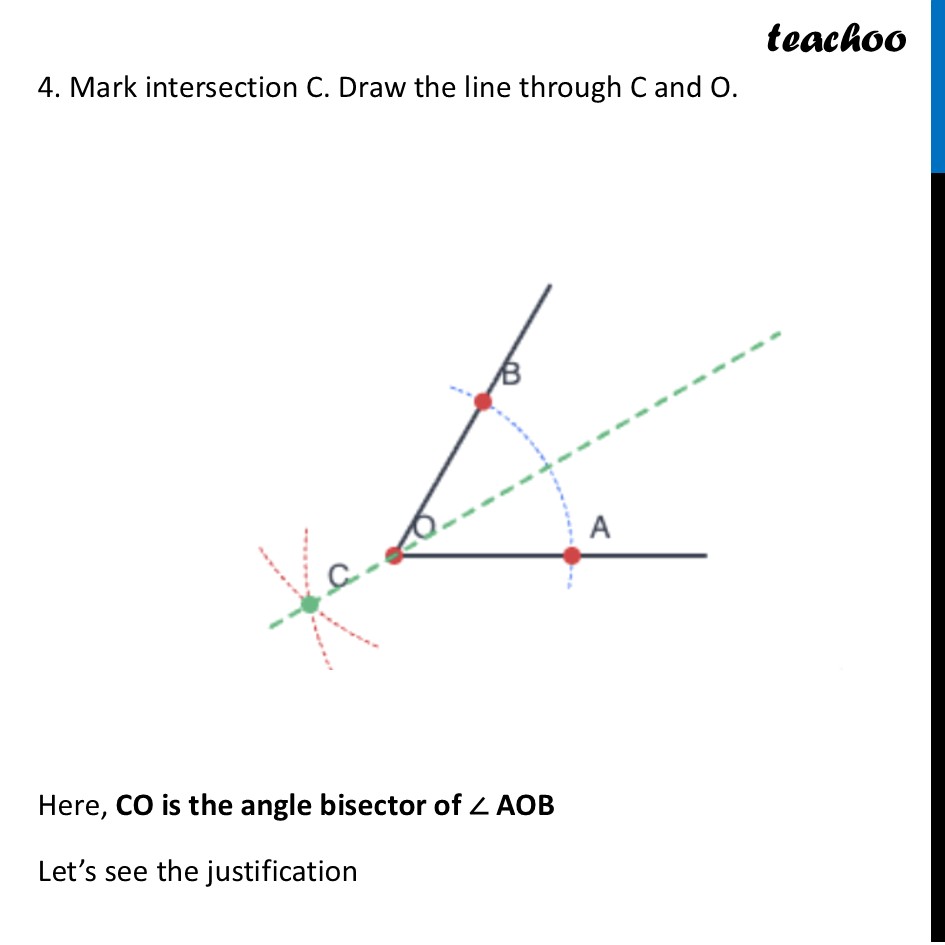
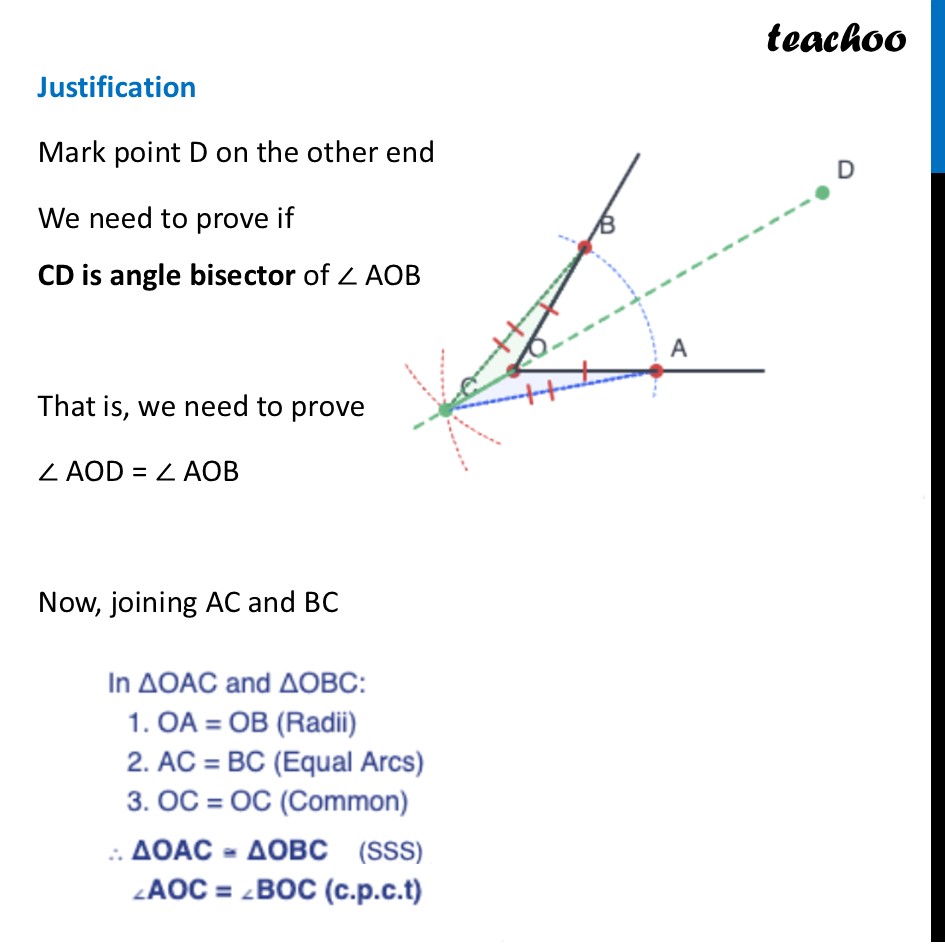
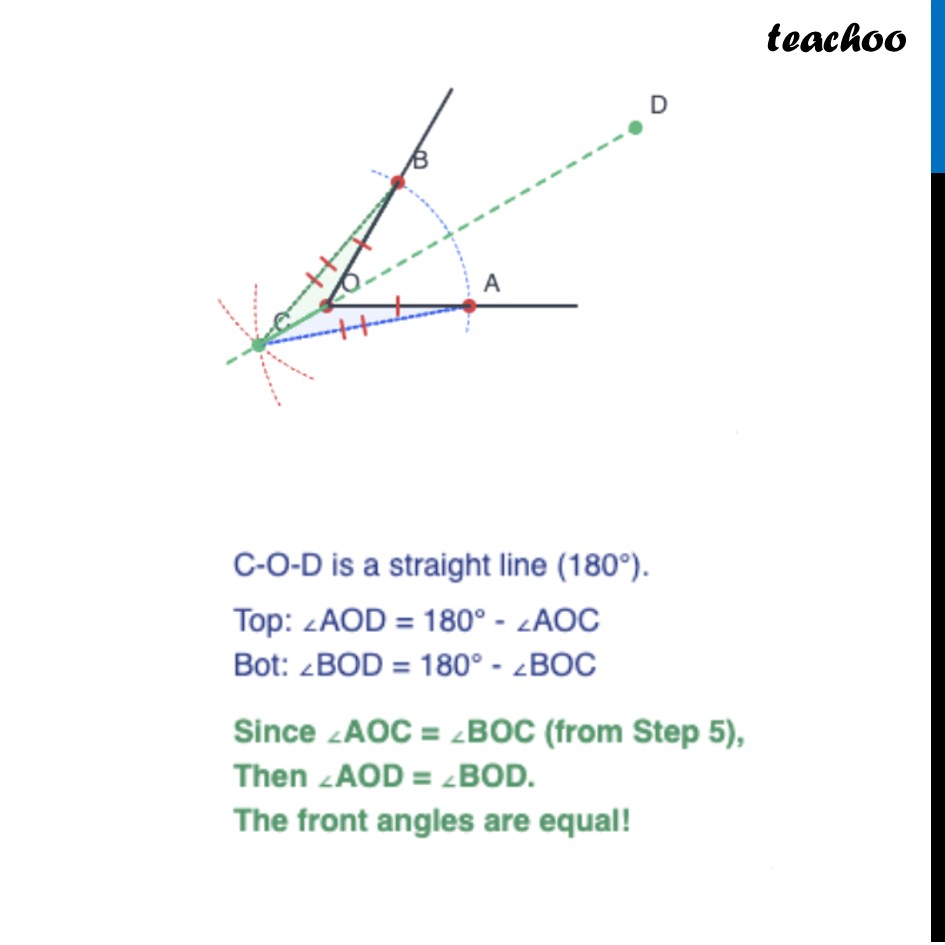
Question 3 In Step 2 of angle bisection, if arcs of equal radius are drawn on the other side, as shown in the figure, will the line OC still be an angle bisector? Explore this through construction, and then justify your answer.Yes, it will still be an angle bisector. This is because of Symmetry. Whether the crossing point C is far out or close in (or even on the "other side" of the chord), it still lies on the precise middle path between the two arms. As long as the distance from the two arm points (A and B) to the crossing point (C) is equal, point C will always land exactly on the bisector line. As long as the distance from the two arm points (A and B) to the crossing point (C) is equal, point C will always land exactly on the bisector line. Exploring through Construction Construct an angle Draw an arc of any radius, intersecting lines at A & B 3. Draw arcs from A and B using a radius LARGER than OA This forces them to cross 'behind' O. 4. Mark intersection C. Draw the line through C and O. Here, CO is the angle bisector of ∠ AOB Let’s see the justification Justification Mark point D on the other end We need to prove if CD is angle bisector of ∠ AOB That is, we need to prove ∠ AOD = ∠ AOB Now, joining AC and BC Thus, we proved the outer angles ∠ AOC = ∠ BOC C-O-D is a straight line . Top: Bot: Since (from Step 5), Then . The front angles are equal!