Question 1 - Page 129 - Shortcut for Divisibility by 11 - Chapter 5 Class 8 - Number Play (Ganita Prakash)

Transcript

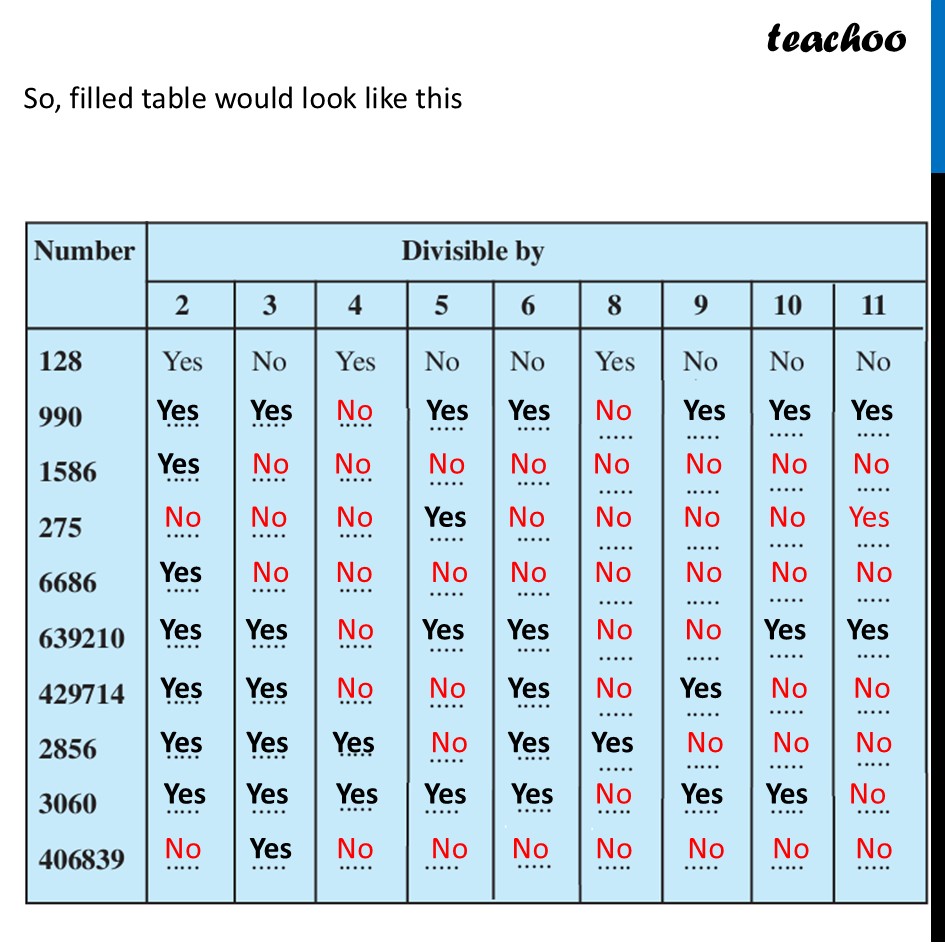
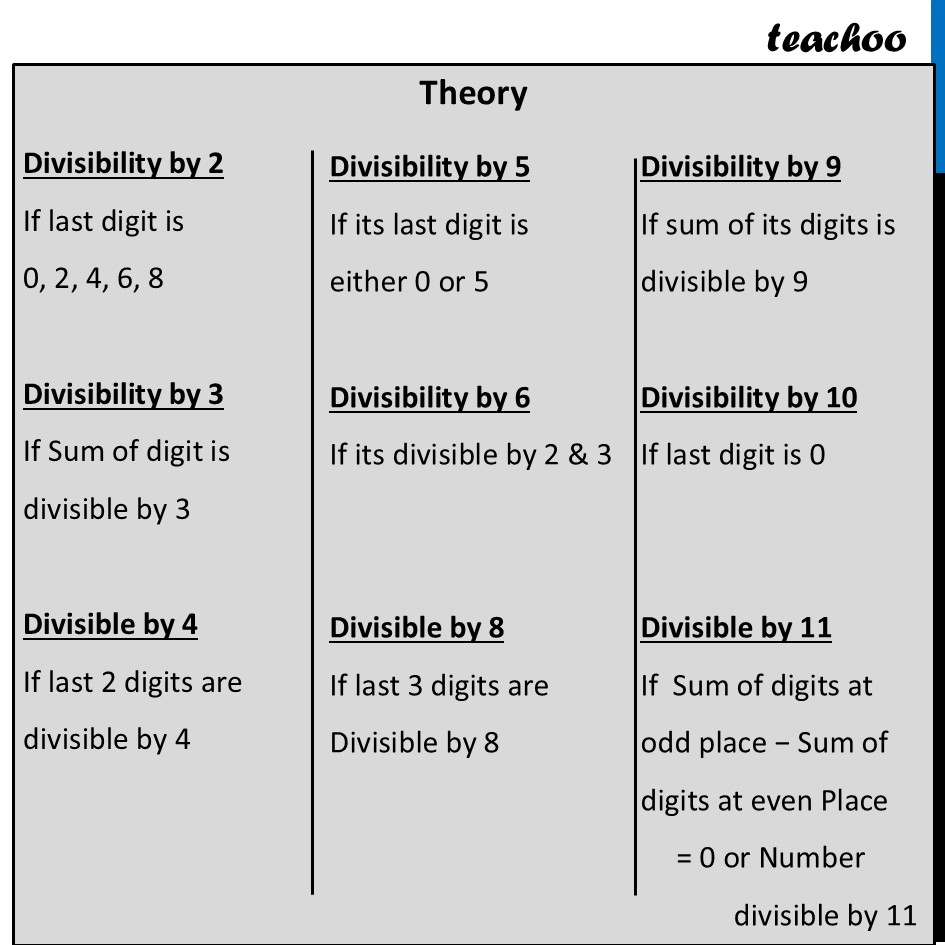
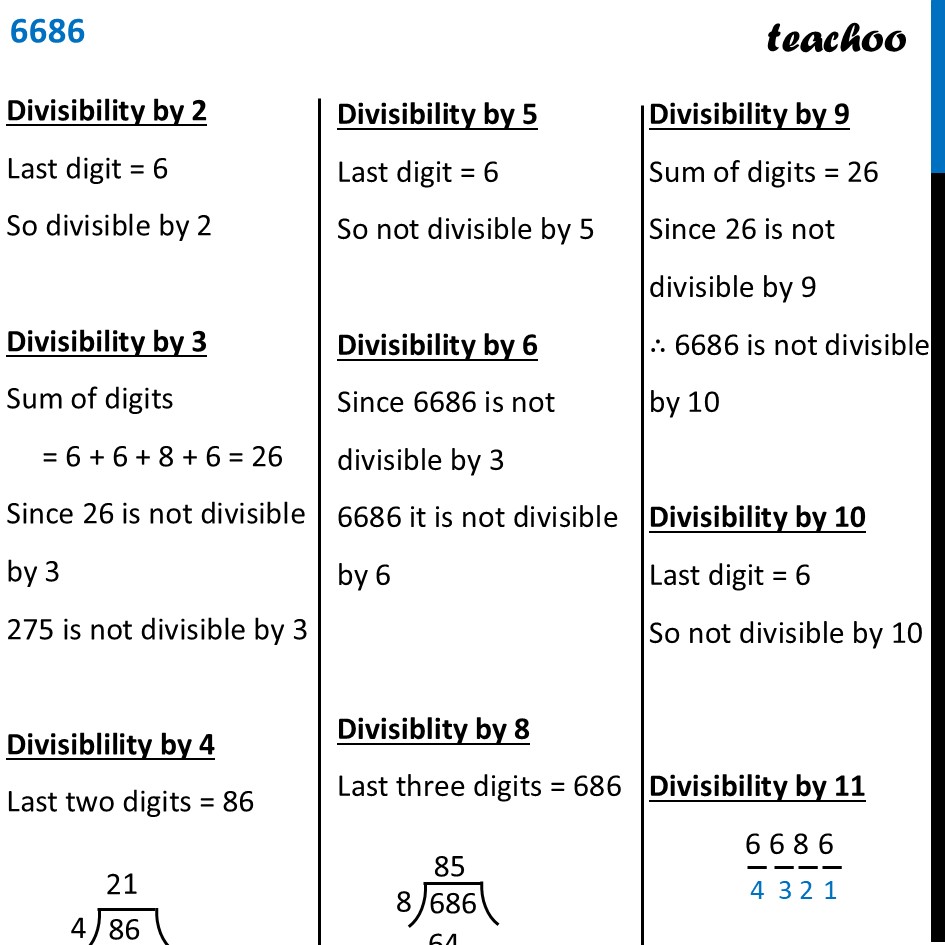
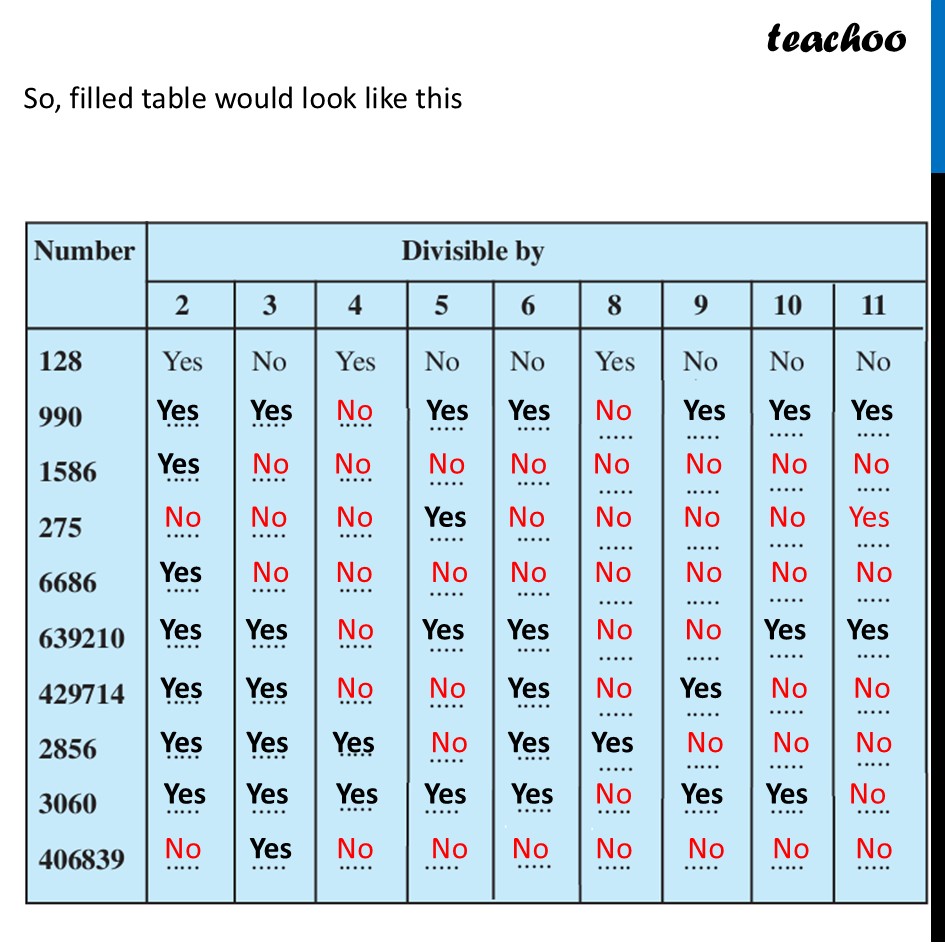
Question 1 - Page 129 Fill in the following table. Find a quick way to do this?So, filled table would look like this Number Divisible by 2 3 4 5 6 8 9 10 11 128 Yes No Yes No No Yes No No No 990 Yes Yes No Yes Yes No Yes Yes Yes 1586 Yes No No No No No No No No 275 No No No Yes No No No No Yes 6686 Yes No No No No No No No No 639210 Yes Yes No Yes Yes No No Yes Yes 429714 Yes Yes No No Yes No Yes No No 2856 Yes Yes Yes No Yes Yes No No No 3060 Yes Yes Yes Yes Yes No Yes Yes No 406839 No Yes No No No No No No NoNumber Divisible by 2 3 4 5 6 8 9 10 11 128 Yes No Yes No No Yes No No No 990 Yes Yes No Yes Yes No Yes Yes Yes 1586 Yes No No No No No No No No 275 No No No Yes No No No No Yes 6686 Yes No No No No No No No No 639210 Yes Yes No Yes Yes No No Yes Yes 429714 Yes Yes No No Yes No Yes No No 2856 Yes Yes Yes No Yes Yes No No No 3060 Yes Yes Yes Yes Yes No Yes Yes No 406839 No Yes No No No No No No NoDivisibility by 2 If last digit is 0, 2, 4, 6, 8 Divisibility by 3 If Sum of digit is divisible by 3 Divisible by 4 If last 2 digits are divisible by 4 Divisibility by 5 If its last digit is either 0 or 5 Divisibility by 6 If its divisible by 2 & 3 Divisible by 8 If last 3 digits are Divisible by 8 Divisibility by 9 If sum of its digits is divisible by 9 Divisibility by 10 If last digit is 0 Divisible by 11 If Sum of digits at odd place − Sum of digits at even Place = 0 or Number divisible by 11 Divisibility by 2 Since last digit is 0, It is divisible by 2 Divisibility by 3 Sum of digits = 9 + 9 + 0 = 18 Since 18 is divisible by 3 990 is divisible 3 Divisiblility by 4 Last 2 digits = 90 Since 90 is not divisible by 4 990 is not divisible by 4 Divisibility by 5 Since last digit is 0 It is divisible by 5 Divisibility by 6 Since it is divisible by 2 & 3 It is divisible by 6 Divisiblity by 8 Last 3 digits = 990 ∴ 990 is not divisible by 8 Divisibility by 9 Sum of digits = 9 + 9 + 0 = 18 Since 18 is divisible by 9 990 is divisible by 9 Divisibility by 10 Since last digit is 0 It is divisible by 10 Divisible by 11 990 Sum of odd digits = 0 + 9 = 9 Sum of even digits = 9 Difference = 9 − 9 = 0 Since difference is 0 It is divisible by 11 Divisibility by 2 Last digit is 6, so divisible by 2 Divisibility by 3 Sum of digits = 1 + 5 + 8 + 6 = 20 Since 20 is not divisible by 3 ∴ 1586 is not divisible by 3 Divisiblility by 4 Last 2 digits = 86 Since 86 is not divisible by 4 ∴ 1586 is not divisible by 4 Divisibility by 5 Last digit is 6 So 1586 is not divisible by 5 Divisibility by 6 1586 is not divisible by 3 ∴ 1586 is not divisible by 6 Divisiblity by 8 Last 3 digits = 586 Since 586 is not divisible by 8 ∴1586 is not divisible by 8 Divisibility by 9 Sum of digits = 1 + 5 + 8 + 6 = 20 Since 20 is not divisible by 9 1586 is not divisible by 9 Divisibility by 10 Last digit is 6 So 1586 is not divisible by 10 Divisible by 11 1586 Sum of odd digits = 6 + 5 = 11 Sum of even digits = 1 + 8 = 9 Difference = 11 − 9 = 2 Since 2 is not divisible by 11 So 1586 is not divisible by 11 Divisibility by 2 Last digit = 5 ∴ It is not divisible by 2 Divisibility by 3 Sum of digits = 2 + 7 + 5 = 14 Since 14 is not divisible by 3 275 is not divisible by 3 Divisiblility by 4 Last 2 digits = 75 Since 75 is not divisible by 4 275 is not divisible by 4 Divisibility by 5 Last digit is 5 So divisible by 5 Divisibility by 6 Since 275 is not divisible by 2 & 3 It is not divisible by 6 Divisiblity by 8 Last 3 digits = 275 ∴ 275 is not divisible by 8 Divisibility by 9 Sum of digits = 2 + 7 + 5 = 14 Since 14 is not divisible by 9 ∴ 275 is not divisible by 9 Divisibility by 10 Last digit = 5 So not divisible by 10 Divisible by 11 275 Sum of odd digits = 5 + 2 = 7 Sum of even digits = 7 Difference = 0 Since difference is 0 ∴ 275 is divisible by 11 Divisibility by 2 Last digit = 6 So divisible by 2 Divisibility by 3 Sum of digits = 6 + 6 + 8 + 6 = 26 Since 26 is not divisible by 3 275 is not divisible by 3 Divisiblility by 4 Last two digits = 86 Since 86 is not divisible by 4 6686 is not divisible by 4 Divisibility by 5 Last digit = 6 So not divisible by 5 Divisibility by 6 Since 6686 is not divisible by 3 6686 it is not divisible by 6 Divisiblity by 8 Last three digits = 686 Since 686 is not divisible by 8 ∴ 6686 is not divisible by 8 Divisibility by 9 Sum of digits = 26 Since 26 is not divisible by 9 ∴ 6686 is not divisible by 10 Divisibility by 10 Last digit = 6 So not divisible by 10 Divisibility by 11 6686 Sum of odd digits = 6 + 6 = 12 Sum of even digits = 8 + 6 = 14 Difference = 14 − 12 = 2 Since 2 is not divisible by 11 ∴ 6686 is not divisible by 11 Divisibility by 2 Last digit = 0 So divisible by 2 Divisibility by 3 Sum of digits = 6 + 3 + 9 + 2 + 1 + 0 = 21 Since 21 is divisible by 3 639210 is divisible by 3 Divisiblility by 4 Last two digits = 10 Since 10 is not divisible by 4 ∴ 639210 is not divisible by 4 Divisibility by 5 Last digit = 0 So, divisible by 5 Divisibility by 6 Since 639210 is divisible by both 2 & 3 It is also divisible by 6 Divisiblity by 8 Last 3 digits = 210 Since 210 is not divisible by 8 ∴ 639210 is not divisible by 8 Divisibility by 9 Sum of digits = 6 + 3 + 9 + 2 + 1 + 0 = 21 Since 21 is not divisible by 9 ∴ 639210 is not divisible by 9 Divisibility by 10 Last digit = 0 So divisible by 10 Divisibility by 11 639210 Sum of odd digits = 0 + 2 + 3 = 5 Sum of even digits = 1 + 9 + 6 = 16 Difference = 16 − 5 = 11 Since difference is 11 ∴ 639210 is divisible by 11 Divisibility by 2 Last digit = 4 ∴ It is divisible by 2 Divisibility by 3 Sum of digits = 4 + 2 + 9 + 7 + 1 + 4 = 27 Since 27 is divisible by 3 429714 is divisible by 3 Divisibilility by 4 Last two digits = 14 Since 14 is not divisible by 4 ∴ 429714 is not divisible by 4 Divisibility by 5 Last digit = 4 So 429714 is not divisible by 5 Divisibility by 6 Since it is divisible by both 2 & 3 It is also divisible by 6 Divisibility by 8 Last 3 digits = 714 Since 714 is not divisible by 8 ∴ 429714 is not divisible by 8 Divisibility by 9 Sum of digits = 4 + 2 + 9 + 7 + 1 + 4 = 27 Since 27 is divisible by 9 ∴ 429714 is divisible by 9 Divisibility by 10 Last digit = 4 So 429714 is not divisible by 10 Divisibility by 11 429714 Sum of odd digits = 2 + 7 + 4 = 13 Sum of even digits = 4 + 9 + 1 = 14 Difference = 14 − 13 = 1 Since 1 is not divisible by 11 ∴ 429714 is not divisible by 11 Divisibility by 2 Last digit is 6, so divisible by 2 Divisibility by 3 Sum of digits = 2 + 8 + 5 + 6 = 21 Since 21 is divisible by 3 ∴ 2856 is divisible by 3 Divisiblility by 4 Last 2 digits = 56 Since 56 is divisible by 4 ∴ 2856 is divisible by 4 Divisibility by 5 Last digit is 6 So 1586 is not divisible by 5 Divisibility by 6 2856 is divisible by 2 & 3 ∴ 2856 is divisible by 6 Divisiblity by 8 Last 3 digits = 856 Since 856 is divisible by 8 ∴2856 is divisible by 8 Divisibility by 9 Sum of digits = 2 + 8 + 5 + 6 = 21 Since 21 is not divisible by 9 2856 is not divisible by 9 Divisibility by 10 Last digit is 6 So 2856 is not divisible by 10 Divisible by 11 2856 Sum of odd digits = 8 + 6 = 14 Sum of even digits = 2 + 5 = 7 Difference = 14 − 7 = 7 Since 7 is not divisible by 11 So 2856 is not divisible by 11 Divisibility by 2 Last digit = 0 So divisible by 2 Divisibility by 3 Sum of digits = 3 + 0 + 6 + 0 = 9 Since 9 is divisible by 3 3060 is divisible by 3 Divisiblility by 4 Last two digits = 60 Since 60 is divisible by 4 ∴ 3060 is divisible by 4 Divisibility by 5 Last digit = 0 So, divisible by 5 Divisibility by 6 Since 3060 is divisible by both 2 & 3 It is also divisible by 6 Divisiblity by 8 Last 3 digits = 060 = 60 Since 3060is not divisible by 8 ∴ 639210 is not divisible by 8 Divisibility by 9 Sum of digits = 3 + 0 + 6 + 0 = 9 Since 9 is divisible by 9 ∴ 3060 is divisible by 9 Divisibility by 10 Last digit = 0 So divisible by 10 Divisibility by 11 3060 Sum of odd digits = 0 + 0 = 0 Sum of even digits = 3 + 6 = 9 Difference = 9 – 0 = 9 Since difference is not 0 nor multiple of 11 ∴ 3060 is not divisible by 11 Divisibility by 2 Last digit = 9 ∴ It is not divisible by 2 Divisibility by 3 Sum of digits = 4 + 0 + 6 + 8 + 3 + 9 = 30 Since 30 is divisible by 3 ∴ It is divisible by 3 Divisiblility by 4 Last 2 digits = 39 Since 39 is not divisible by 4 406839 is not divisible by 4 Divisibility by 5 Last digit is 9 ∴ It is not divisible by 5 Divisibility by 6 Since 406839 is not divisible by 3 It is not divisible by 6 Divisiblity by 8 Last 3 digits = 839 ∴ 406839 is not divisible by 8 Divisibility by 9 Sum of digits = 4 + 0 + 6 + 8 + 3 + 9 = 30 Since 30 is not divisible by 9 ∴ It is not divisible by 9 Divisibility by 10 Last digit = 10 ∴ It is not divisible by 10 Divisible by 11 406839 Sum of odd digits = 9 + 8 + 0 = 17 Sum of even digits = 3 + 6 + 4 = 13 Difference = 4 Since difference is not 0 nor multiple of 11 ∴ It is divisible by 11 So, filled table would look like this Number Divisible by 2 3 4 5 6 8 9 10 11 128 Yes No Yes No No Yes No No No 990 Yes Yes No Yes Yes No Yes Yes Yes 1586 Yes No No No No No No No No 275 No No No Yes No No No No Yes 6686 Yes No No No No No No No No 639210 Yes Yes No Yes Yes No No Yes Yes 429714 Yes Yes No No Yes No Yes No No 2856 Yes Yes Yes No Yes Yes No No No 3060 Yes Yes Yes Yes Yes No Yes Yes No 406839 No Yes No No No. No No No No