Question 1 - Figure it out - Page 94 - Chapter 4 Class 8 - Quadrilaterals (Ganita Prakash)

Transcript

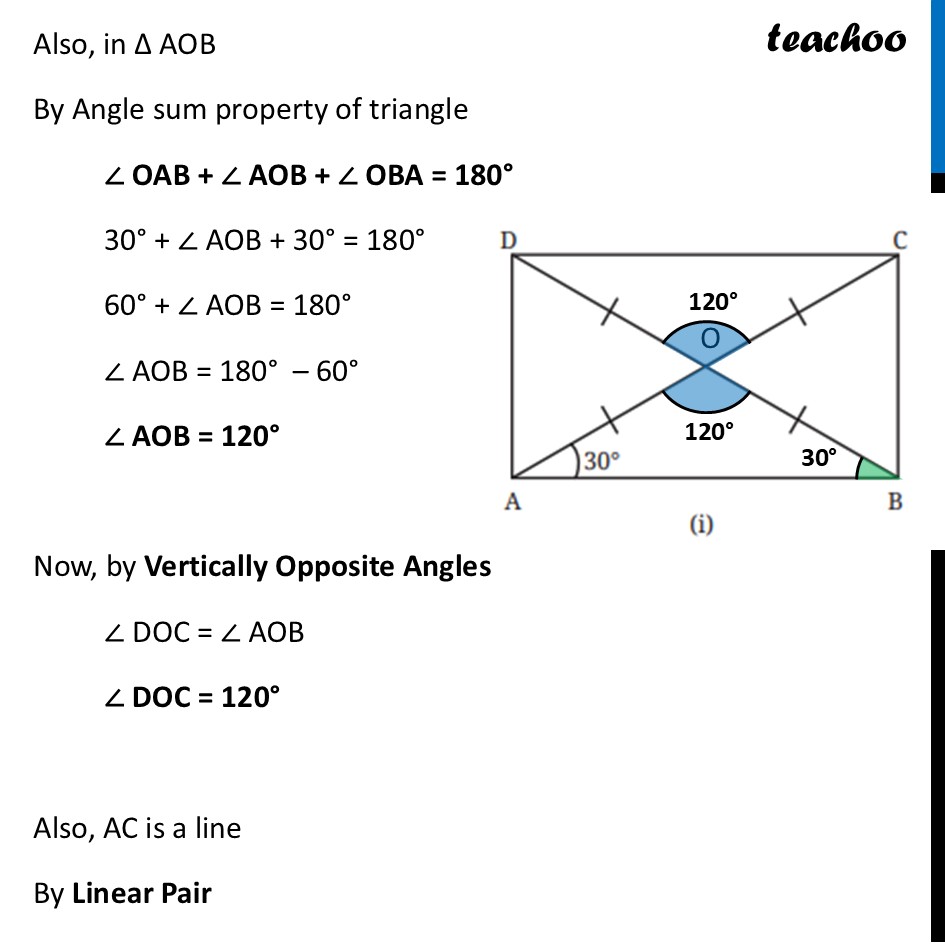
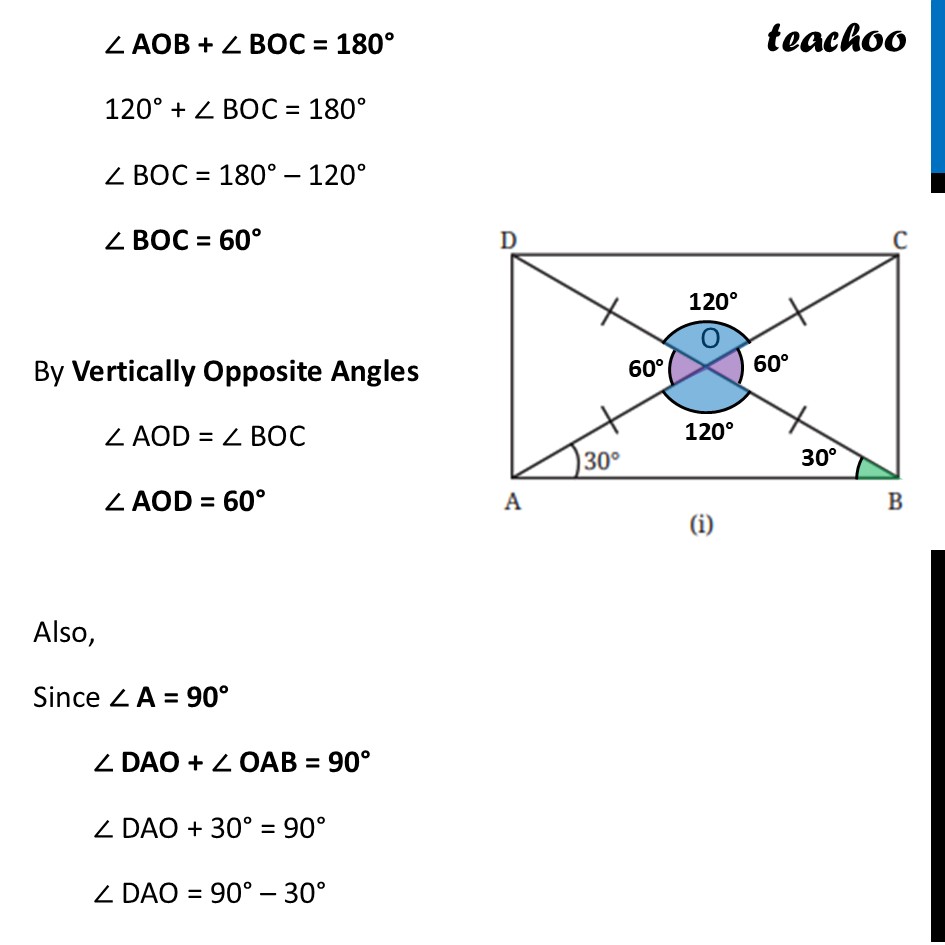
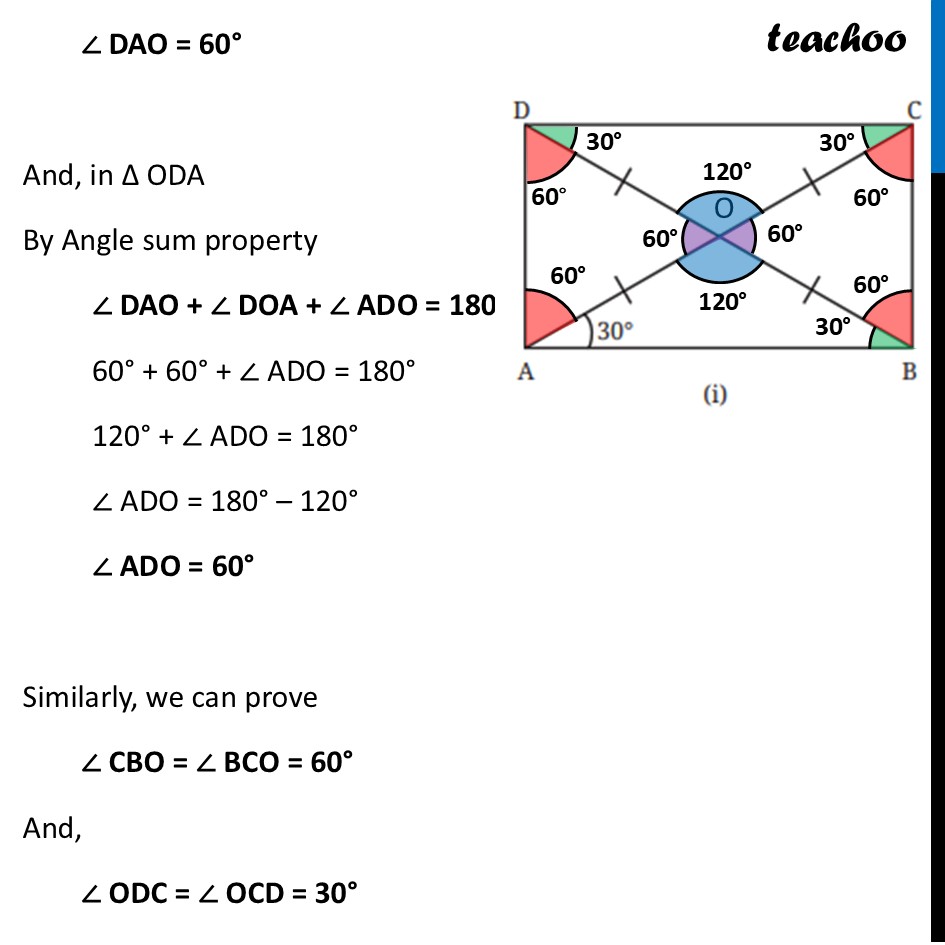
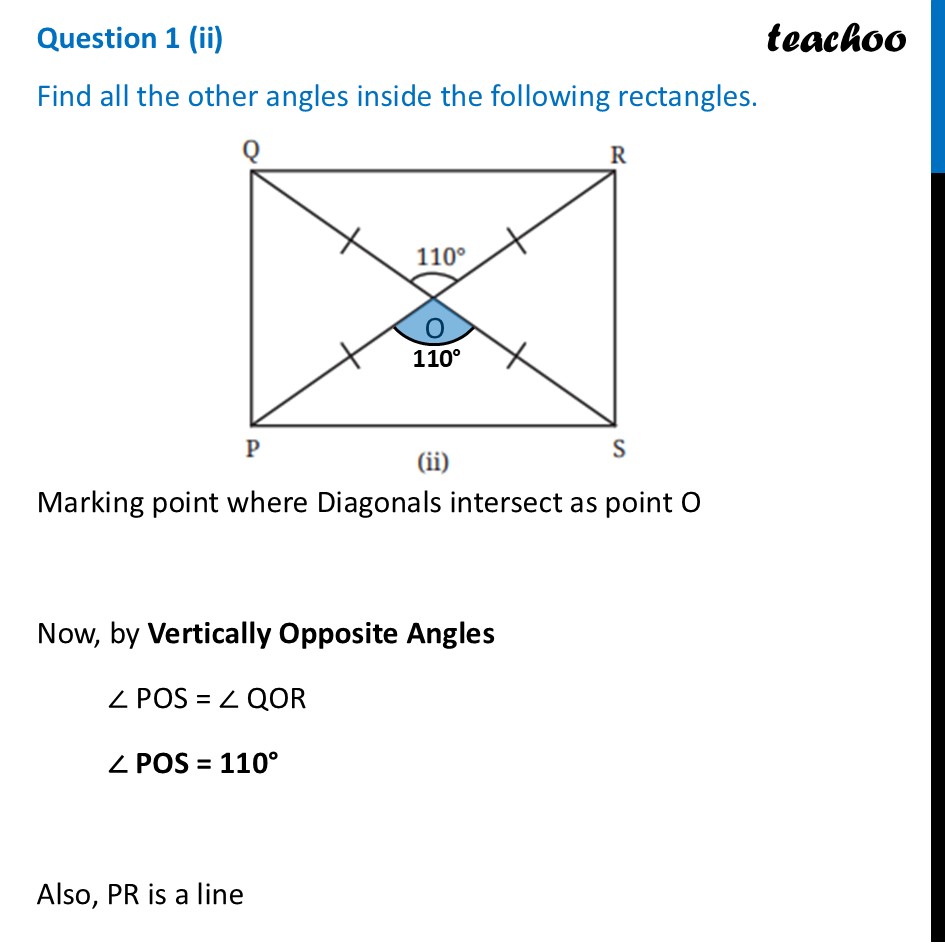
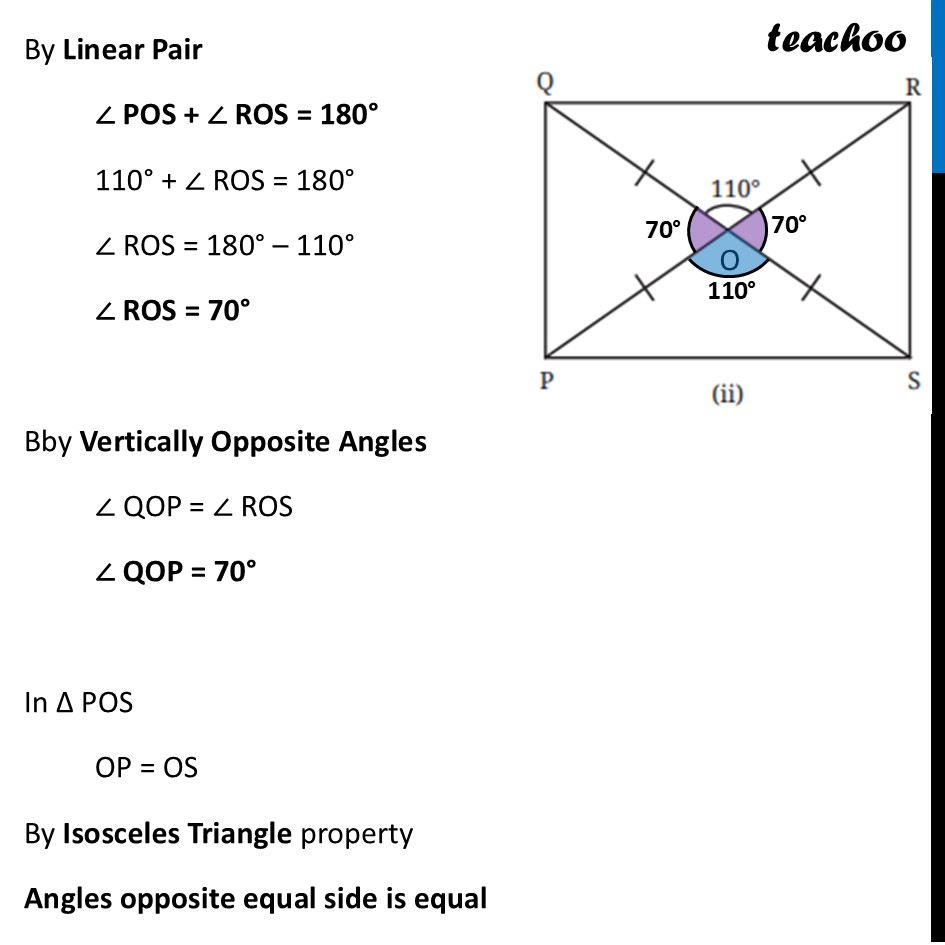
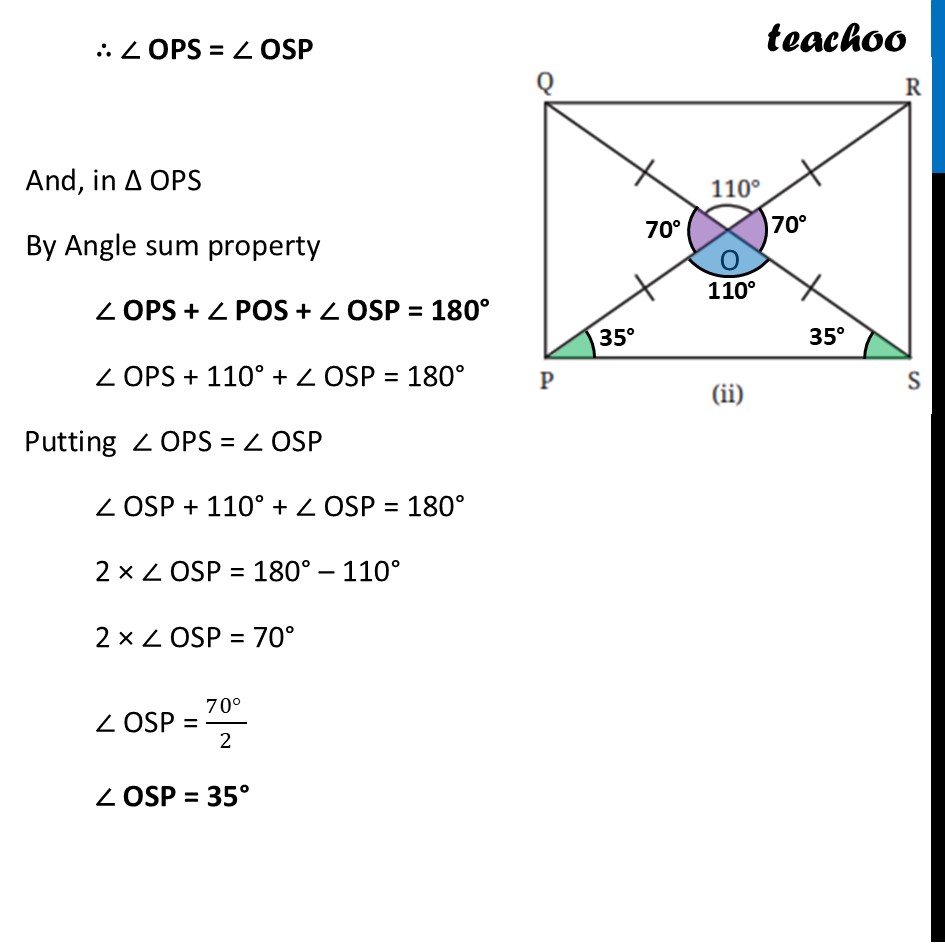
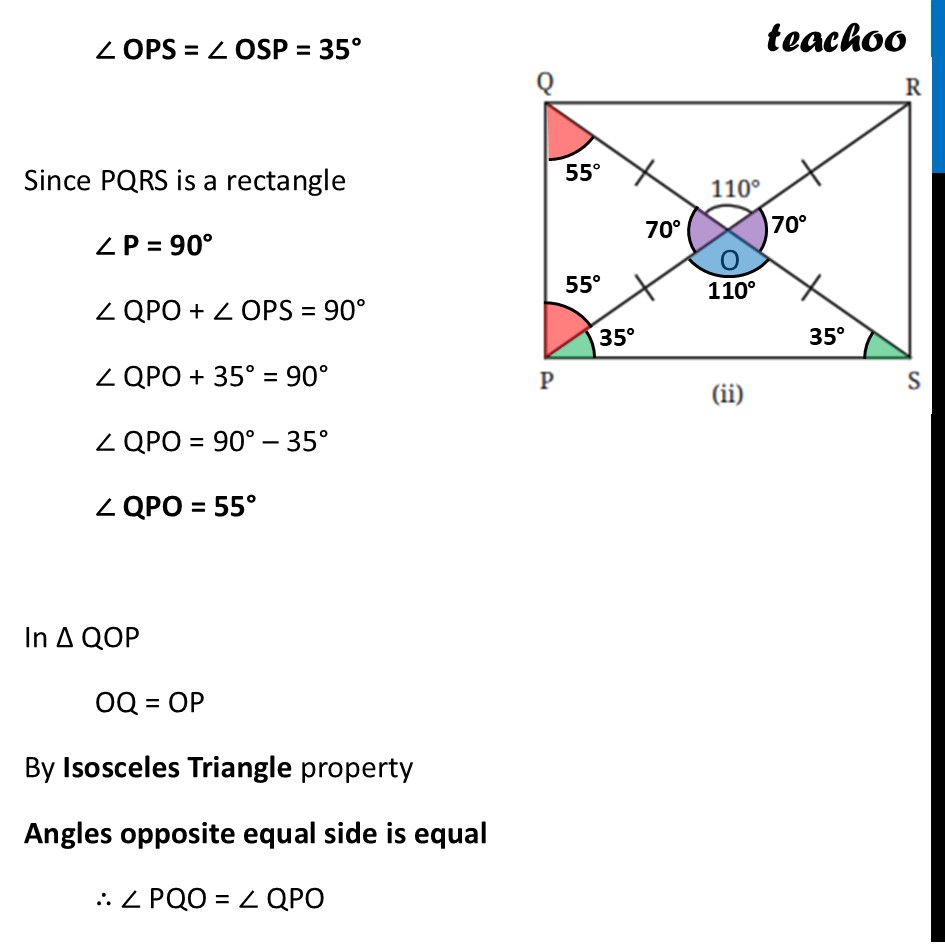
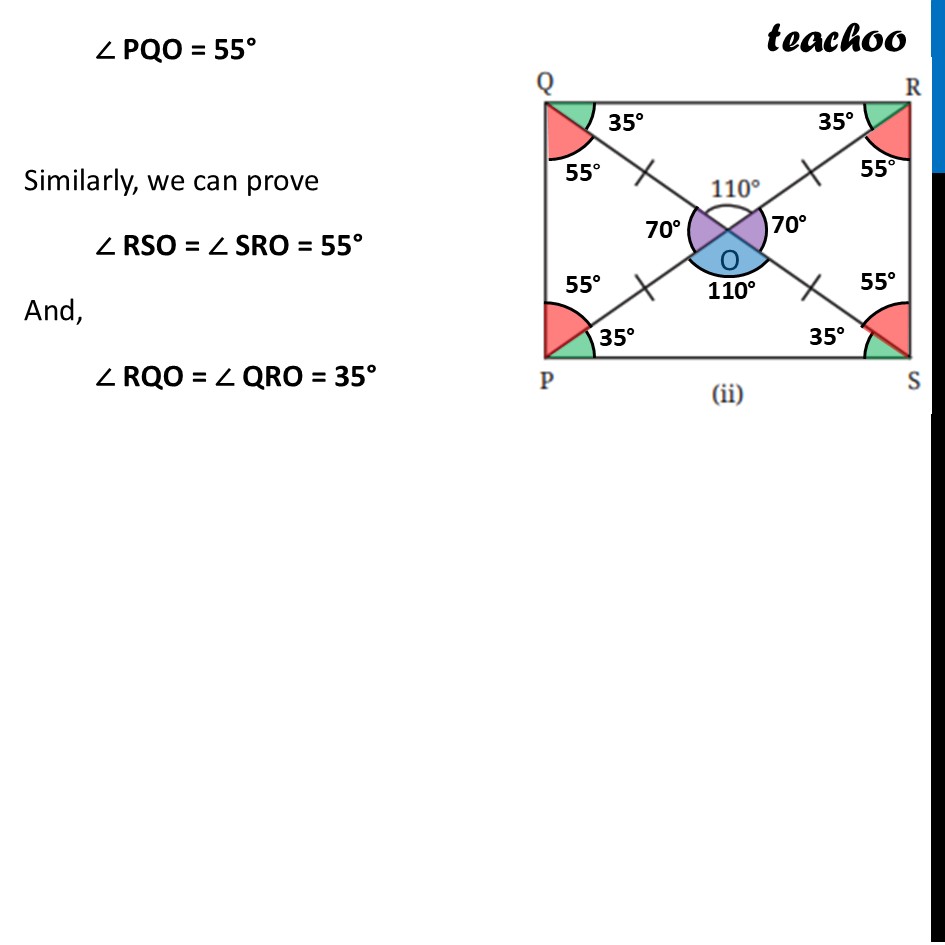
Question 1 (i) Find all the other angles inside the following rectangles.Marking point where Diagonals intersect as point O In ∆ AOB OA = OB By Isosceles Triangle property Angles opposite equal side is equal ∴ ∠ OBA = ∠ OAB ∠ OBA = 30° Also, in ∆ AOB By Angle sum property of triangle ∠ OAB + ∠ AOB + ∠ OBA = 180° 30° + ∠ AOB + 30° = 180° 60° + ∠ AOB = 180° ∠ AOB = 180° – 60° ∠ AOB = 120° Now, by Vertically Opposite Angles ∠ DOC = ∠ AOB ∠ DOC = 120° Also, AC is a line By Linear Pair ∠ AOB + ∠ BOC = 180° 120° + ∠ BOC = 180° ∠ BOC = 180° – 120° ∠ BOC = 60° By Vertically Opposite Angles ∠ AOD = ∠ BOC ∠ AOD = 60° Also, Since ∠ A = 90° ∠ DAO + ∠ OAB = 90° ∠ DAO + 30° = 90° ∠ DAO = 90° – 30° ∠ DAO = 60° And, in ∆ ODA By Angle sum property ∠ DAO + ∠ DOA + ∠ ADO = 180° 60° + 60° + ∠ ADO = 180° 120° + ∠ ADO = 180° ∠ ADO = 180° – 120° ∠ ADO = 60° Similarly, we can prove ∠ CBO = ∠ BCO = 60° And, ∠ ODC = ∠ OCD = 30° Question 1 (ii) Find all the other angles inside the following rectangles.Marking point where Diagonals intersect as point O Now, by Vertically Opposite Angles ∠ POS = ∠ QOR ∠ POS = 110° Also, PR is a line By Linear Pair ∠ POS + ∠ ROS = 180° 110° + ∠ ROS = 180° ∠ ROS = 180° – 110° ∠ ROS = 70° Bby Vertically Opposite Angles ∠ QOP = ∠ ROS ∠ QOP = 70° In ∆ POS OP = OS By Isosceles Triangle property Angles opposite equal side is equal ∴ ∠ OPS = ∠ OSP And, in ∆ OPS By Angle sum property ∠ OPS + ∠ POS + ∠ OSP = 180° ∠ OPS + 110° + ∠ OSP = 180° Putting ∠ OPS = ∠ OSP ∠ OSP + 110° + ∠ OSP = 180° 2 × ∠ OSP = 180° – 110° 2 × ∠ OSP = 70° ∠ OSP = (70° )/2 ∠ OSP = 35° ∠ OPS = ∠ OSP = 35° Since PQRS is a rectangle ∠ P = 90° ∠ QPO + ∠ OPS = 90° ∠ QPO + 35° = 90° ∠ QPO = 90° – 35° ∠ QPO = 55° In ∆ QOP OQ = OP By Isosceles Triangle property Angles opposite equal side is equal ∴ ∠ PQO = ∠ QPO ∠ PQO = 55° Similarly, we can prove ∠ RSO = ∠ SRO = 55° And, ∠ RQO = ∠ QRO = 35°