


Geometric Progression(GP): Calculation based/Proofs
Geometric Progression(GP): Calculation based/Proofs
Last updated at December 16, 2024 by Teachoo




Transcript
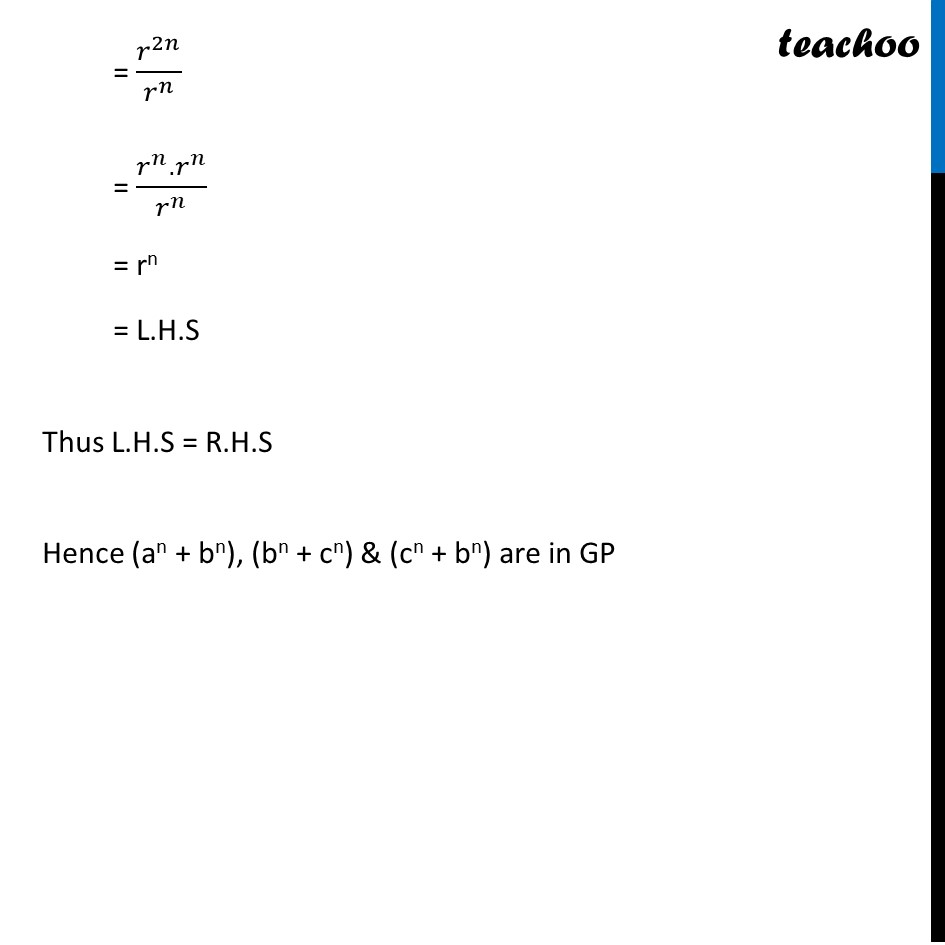
Misc 8 If a, b, c, d are in G.P, prove that (an + bn), (bn + cn), (cn + dn) are in G.P. We know that a, ar , ar2 , ar3, …. are in G.P. with first term a & common ratio r Given a, b, c, d are in G.P. So, a = a b = ar c = ar2 d = ar3 We want to show that (an + bn), (bn + cn), (cn + dn) are in GP i.e. to show common ratio are same (𝑏^𝑛+𝑐^𝑛)/(𝑎^𝑛+𝑏^𝑛 ) = (𝑐^𝑛+𝑑^𝑛)/(𝑏^𝑛+𝑐^𝑛 ) Need to show (𝑏^𝑛+𝑐^𝑛)/(𝑎^𝑛+𝑏^𝑛 ) = (𝑐^𝑛+𝑑^𝑛)/(𝑏^𝑛+𝑐^𝑛 ) Taking L.H.S (𝑏^𝑛+𝑐^𝑛)/(𝑎^𝑛+𝑏^𝑛 ) Putting b = ar , c = ar2 = (〖(𝑎𝑟)〗^𝑛+〖(〖𝑎𝑟〗^2)〗^𝑛)/(𝑎^𝑛+〖(𝑎𝑟)〗^𝑛 ) = (𝑎^𝑛 𝑟^𝑛 + 𝑎^𝑛.𝑟^2𝑛)/(𝑎^𝑛 + 𝑎^𝑛 𝑟^𝑛 ) = (𝑎^𝑛 𝑟^𝑛 (1 +𝑟^𝑛))/(𝑎^𝑛 (1 +𝑟^𝑛)) = rn Taking R.H.S (𝑐^𝑛+𝑑^𝑛)/(𝑏^𝑛+𝑐^𝑛 ) Putting c = ar2, d = ar3, b = ar = (〖(〖𝑎𝑟〗^2)〗^𝑛 + 〖(〖𝑎𝑟〗^3)〗^𝑛)/(〖(𝑎𝑟)〗^𝑛 +〖 (〖𝑎𝑟〗^2)〗^𝑛 ) = (𝑎^𝑛 𝑟^2𝑛+ 𝑎^𝑛 .𝑟^2𝑛)/(𝑎^𝑛 𝑟^𝑛+〖 𝑎〗^𝑛 𝑟^2𝑛 ) = (𝑎^𝑛 (𝑟^2𝑛 + 𝑟^3𝑛))/(𝑎^𝑛 (𝑟^𝑛 + 𝑟^2𝑛)) = ( (𝑟^2𝑛 + 𝑟^3𝑛))/((𝑟^𝑛 + 𝑟^2𝑛)) = (𝑟^2𝑛 (1 + 𝑟))/(𝑟^𝑛 (1 + 𝑟)) = 𝑟^2𝑛/𝑟^𝑛 = (𝑟^𝑛.𝑟^𝑛)/𝑟^𝑛 = rn = rn = L.H.S Thus L.H.S = R.H.S Hence (an + bn), (bn + cn) & (cn + bn) are in GP Hence proved