Playing with Number Patterns

Transcript

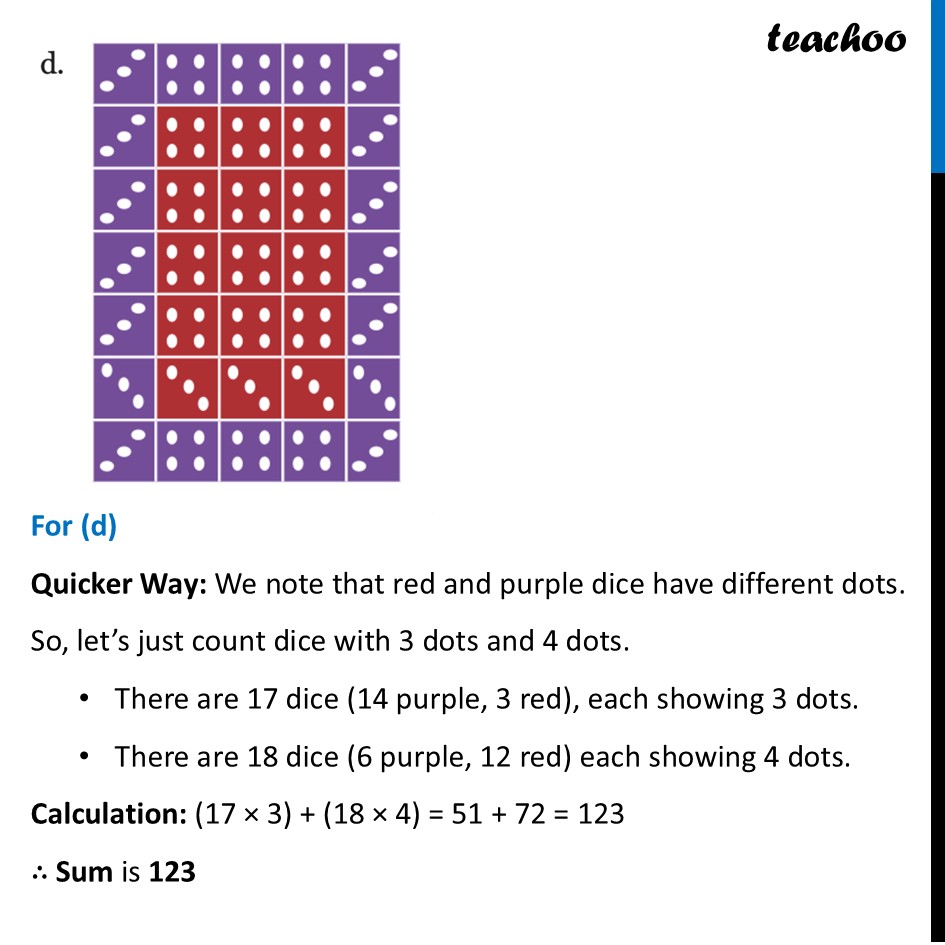
For (b) Quicker Way: Identify the two types of squares: blue squares with 5 dots and teal squares with 1 dot. Count how many of each square there are and multiply by the number of dots. There are 20 blue squares (5 dots each). There are 44 teal squares (1 dot each). Calculation: (20 × 5) + (44 × 1) = 100 + 44 = 144 ∴ Sum is 144 Playing with Number Patterns Here are some numbers arranged in some patterns. Find out the sum of the numbers in each of the below figures. Should we add them one by one or can we use a quicker way? Let’s do this one by one For (a) Quicker Way: The strategy is to count the number of 50s and the number of 40s, multiply each count by its value, and then add the two totals together. There are ten '50s' and twelve '40s’. Calculation: (10 × 50) + (12 × 40) = 500 + 480 = 980 ∴ Sum is 980 For (c) Quicker Way: Count the total number of squares containing '32' and the total number containing '64'. Then multiply and add. There are 32 squares containing the number 32. There are 16 squares containing the number 64. Calculation: (32 × 32) + (16 × 64) = 1024 + 1024 = 2048 ∴ Sum is 2,048 For (e) Quicker Way: The strategy is to count the total occurrences of each number (15, 25, and 35) within the hexagonal pattern and sum their products. Counting: There are eighteen '15s'. There are eighteen '25s'. There are twelve '35s'. Calculation: (18 × 15) + (18 × 25) + (12 × 35) = 270 + 450 + 420 = 1,140 ∴ Sum is 1,140 For (d) Quicker Way: We note that red and purple dice have different dots. So, let’s just count dice with 3 dots and 4 dots. There are 17 dice (14 purple, 3 red), each showing 3 dots. There are 18 dice (6 purple, 12 red) each showing 4 dots. Calculation: (17 × 3) + (18 × 4) = 51 + 72 = 123 ∴ Sum is 123 For (f) Quicker Way: The numbers are in concentric circles. We find the total for each circle and add them all together. Counting: Outer Circle: sixteen '125s' Middle Circle: eight '250s' Inner Circle: four '500s' Center: one '1000' Calculation: (16 × 125) + (8 × 250) + (4 × 500) + 1000 = 2,000 + 2,000 + 2,000 + 1,000 ∴ Sum is 7,000