Ex 14.3, 6 - Chapter 14 Class 10 Statistics (Term 2)

Transcript

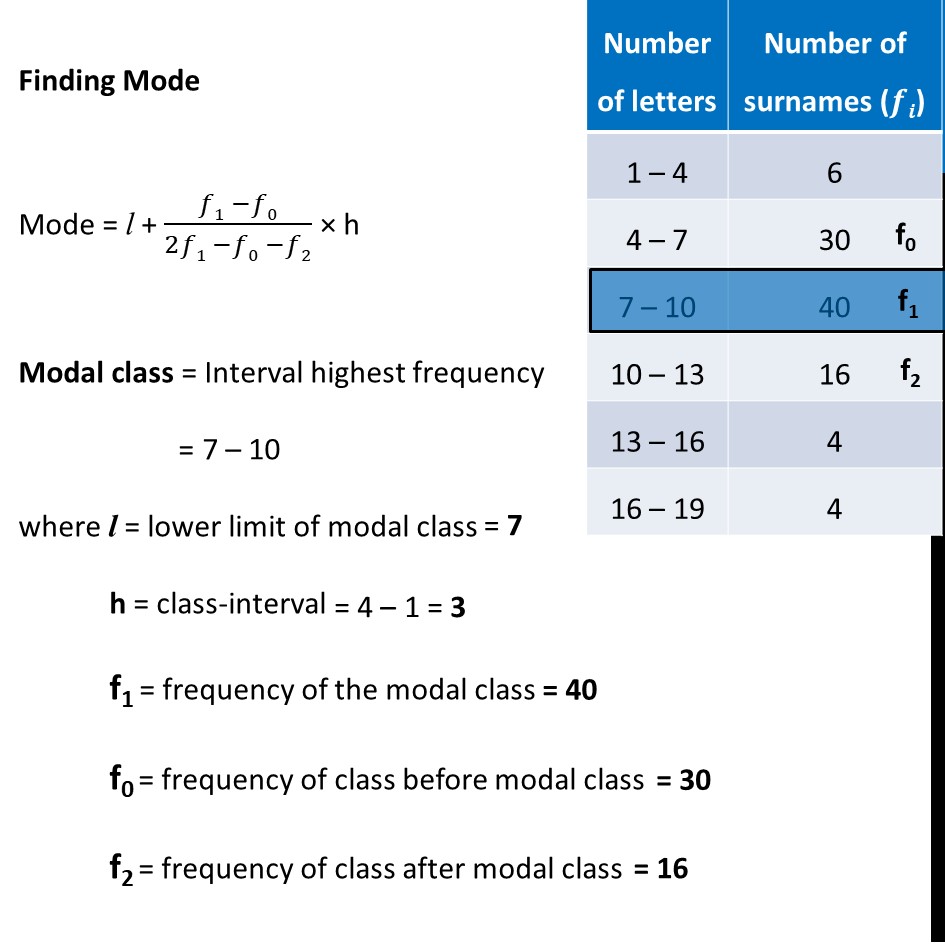
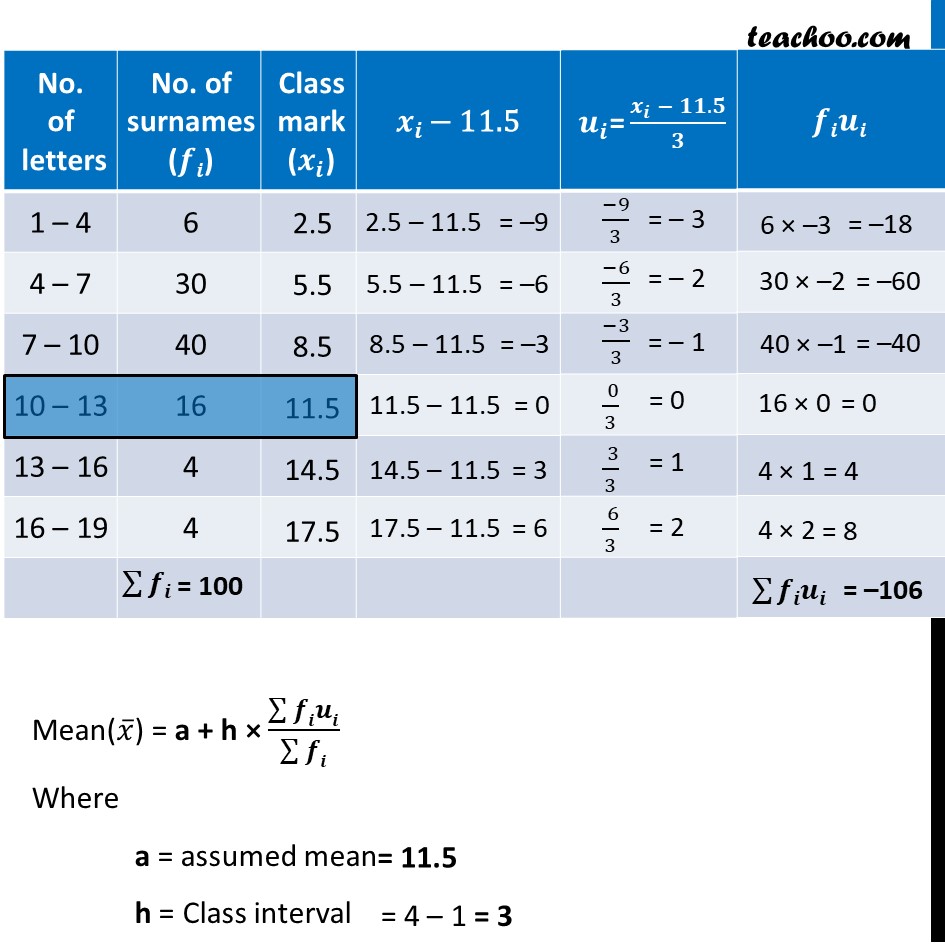
Ex 14.3, 6 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows. Determine the median number of letters in the surnames. Find the mean number of letters in the surnames? Also, find the modal size of the surnames Finding Median Median = l + (𝑁/2 −𝑐𝑓)/𝑓 × h Here, 𝑵/𝟐 ∴ 7 – 10 is median class And, l = h = cf = f = Putting values in formula Median = l + (𝑁/2 −𝑐𝑓)/𝑓 × h = 7 + (𝟓𝟎 − 𝟑𝟔)/𝟒𝟎 × 3 = 7 + 14/40 × 3 = 7 + 1.05 = 8.05 So, Median number of letters is 8.05 Now, we will find mode. Finding Mode Mode = l + (𝑓1 −𝑓0)/(2𝑓1 −𝑓0 −𝑓2) × h Modal class = Interval highest frequency = 7 – 10 where l = lower limit of modal class h = class-interval f1 = frequency of the modal class f0 = frequency of class before modal class f2 = frequency of class after modal class Putting values in formula Mode = 1500 + (𝟒𝟎 −𝟐𝟒)/(𝟐(𝟒𝟎)−𝟐𝟒−𝟑𝟑) × 500 = 7 + (40 −30)/(2(40)−30−16) × 3 = 7 + 10/(80−46) × 3 = 7 + 10/34 × 3 = 7 + 0.88 = 7.88 Thus, Modal number of letters is 7.88 Now, let’s find Mean Mean(𝑥 ̅) = a + h × (∑▒𝒇𝒊𝒖𝒊)/(∑▒𝒇𝒊) Where a = assumed mean h = Class interval = 11.5 Also, ∑▒𝒇𝒊 = 100 ∑▒𝒇𝒊𝒖𝒊 = −106 Putting values in formula Mean(𝑥 ̅) = a + h × (∑▒𝑓𝑖𝑢𝑖)/(∑▒𝑓𝑖) 𝒙 ̅ = 11.5 + 3 × (−𝟏𝟎𝟔)/𝟏𝟎𝟎 𝑥 ̅ = 11.5 – 3.18 𝑥 ̅ = 8.32 Therefore, the Mean is 8.32