Question 4 - Examples - Chapter 11 Class 10 Areas related to Circles

Transcript

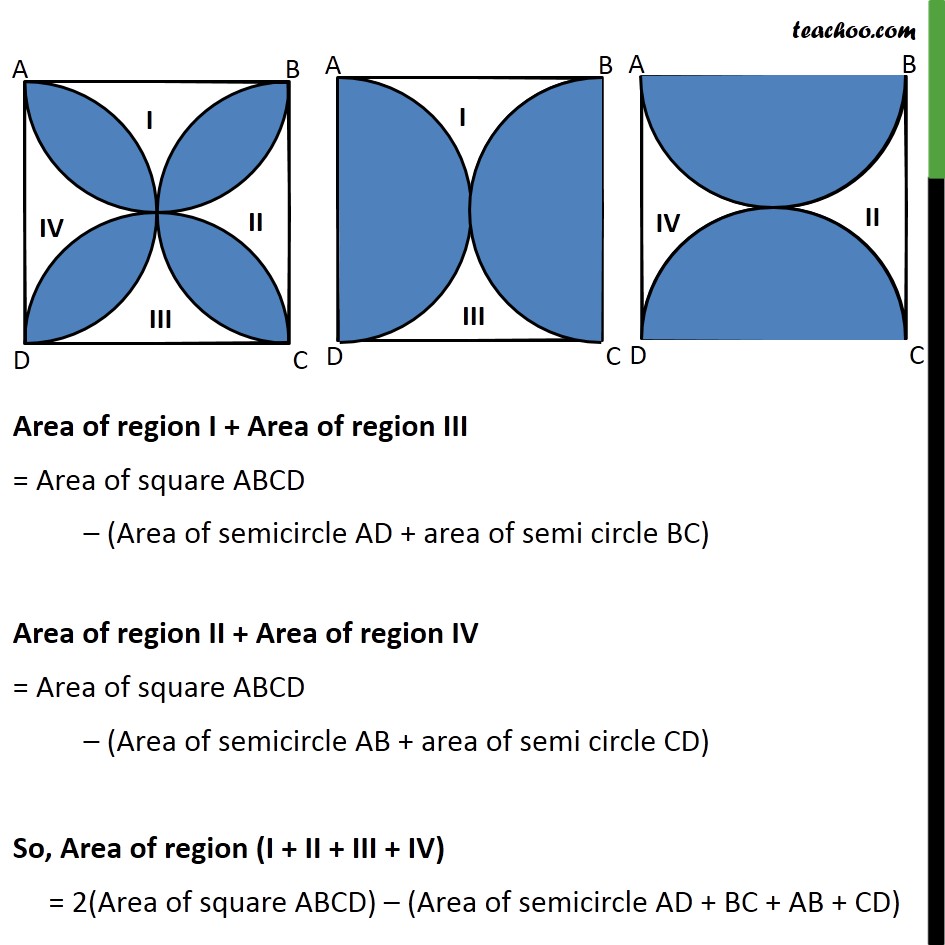
Question 4 (Method 1) Find the area of the shaded design in figure, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. (Use π= 3.14) Given Side of square ABCD = 10 cm Area of square ABCD = (side)2 = (10)2 = 100 cm2 Given semicircle is drawn with side of square as diameter, So, Diameter of semicircle = Side of square = 10 cm Radius of semicircle = 𝑠𝑖𝑑𝑒/2 = 10/2 = 5 cm Area of semi circle AD = 1/2× area of circle = 1/2×πr2 = 1/2×π×(5)2 = (3.14 × 25)/2 Since radius is same for semi-circle AD, BC, AB, CD Area of semi circle AD = Area of semi circle BC = Area of semi circle AB = Area of semi circle CD = (3.14 × 25)/2 Let us mark the unshaded region as I , II, III, and IV. Area of shaded region = Area of ABCD – (Area of I + II + III + IV) Area of region I + Area of region III = Area of square ABCD – (Area of semicircle AD + area of semi circle BC) Area of region II + Area of region IV = Area of square ABCD – (Area of semicircle AB + area of semi circle CD) So, Area of region (I + II + III + IV) = 2(Area of square ABCD) – (Area of semicircle AD + BC + AB + CD) Putting values = 2(100) – ((3.14 × 25)/2 + (3.14 × 25)/2 + (3.14 × 25)/2 + (3.14 × 25)/2) = 200 – 4 × (3.14 × 25)/2 = 200 – 2 × 3.14 × 25 = 200 – 157 = 43 cm2 Now, Area of shaded region = Area of ABCD – (Area of I + II + III + IV) = 100 – 43 = 57 cm2 Hence, area of shaded region = 57 cm2 Question 4 (Method 2) Find the area of the shaded design in figure, where ABCD is a square of side 10 cm and semicircles are drawn with each side of the square as diameter. (Use π= 3.14) Given Side of square ABCD = 10 cm Area of square ABCD = (side)2 = (10)2 = 100 cm2 Given semicircle is drawn with side of square as diameter, So, Diameter of semicircle = Side of square = 10 cm Radius of semicircle = 𝑠𝑖𝑑𝑒/2 = 10/2 = 5 cm Area of semi circle AD = 1/2× area of circle = 1/2×πr2 = 1/2×π×(5)2 = (3.14 × 25)/2 Since radius is same for semi-circle AD, BC, AB, CD Area of semi circle AD = Area of semi circle BC = Area of semi circle AB = Area of semi circle CD = (3.14 × 25)/2 Area of 4 semicircles – Area of shaded region = Area of square ABCD Area of shaded region = Area of 4 semicircles – Area of square ABCD Area of shaded region = 4 × (3.14 × 25)/2 – 100 = 2 × 3.14 × 25 – 100 = 157 – 100 = 57 cm2