Question 4 - Pythagoras Theoram - Proving - Chapter 6 Class 10 Triangles

Transcript

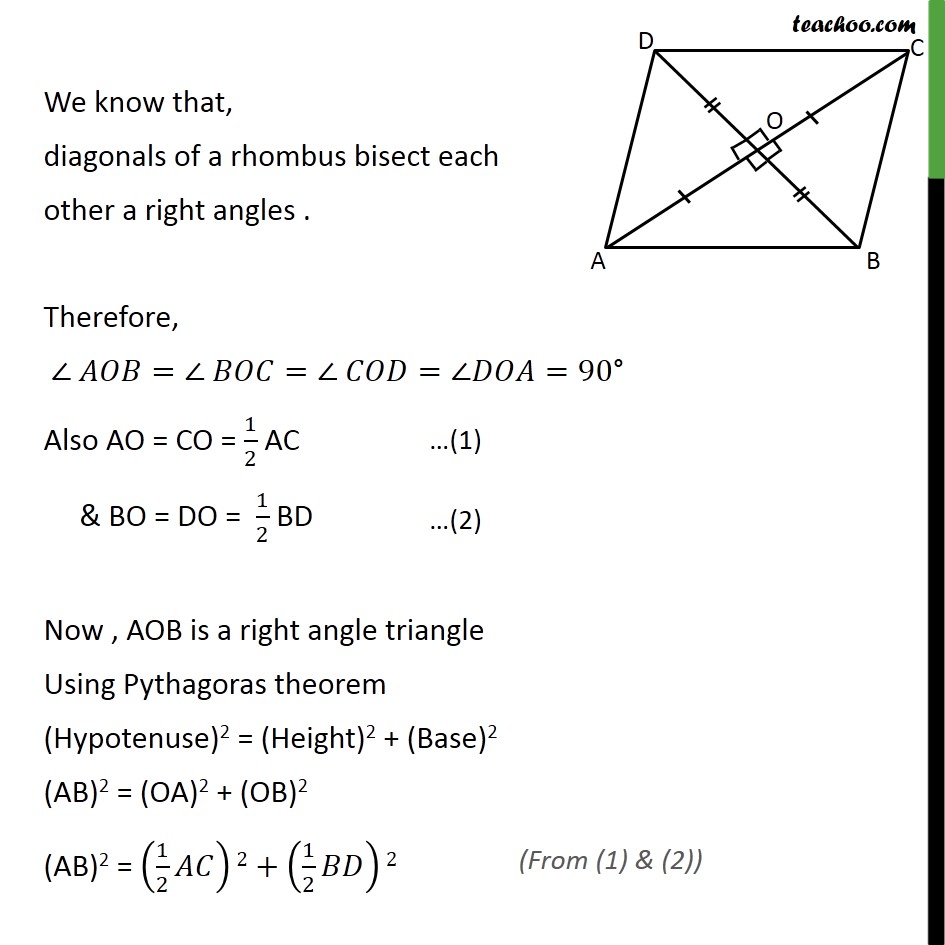
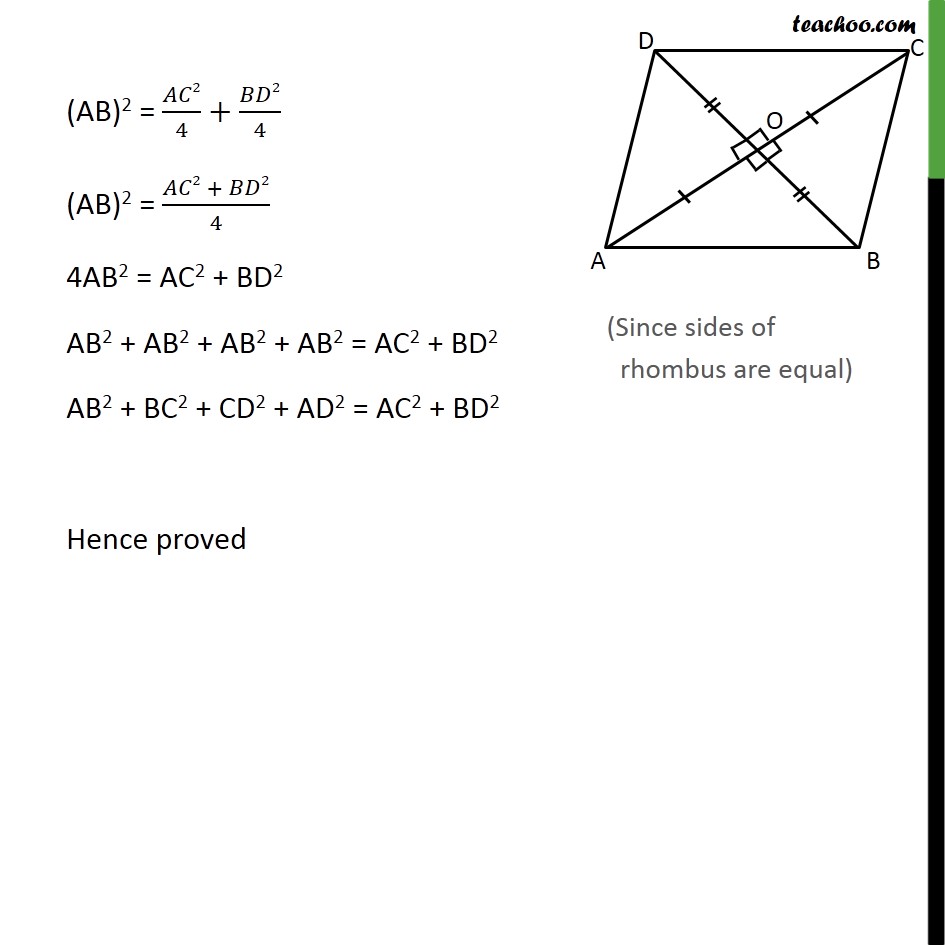
Question7 Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals. Given:- Rhombus ABCD with diagonals AC & BD intersecting at O To prove: Sum of square of all sides = Sum of the squares of it s diagonals AB2 + BC2 + CD2 + AD2 = AC2 + BD2 Proof: Since sides of a rhombus are equal AB = BC = CD = AD We know that, diagonals of a rhombus bisect each other a right angles . Therefore, = = = =90 Also AO = CO = 1/2 AC & BO = DO = 1/2 BD Now , AOB is a right angle triangle Using Pythagoras theorem (Hypotenuse)2 = (Height)2 + (Base)2 (AB)2 = (OA)2 + (OB)2 (AB)2 = (1/2 )2+(1/2 )2 (AB)2 = 2/4+ 2/4 (AB)2 = ( 2 + 2)/4 4AB2 = AC2 + BD2 AB2 + AB2 + AB2 + AB2 = AC2 + BD2 AB2 + BC2 + CD2 + AD2 = AC2 + BD2 Hence proved