

Last updated at Feb. 13, 2025 by Teachoo



Transcript
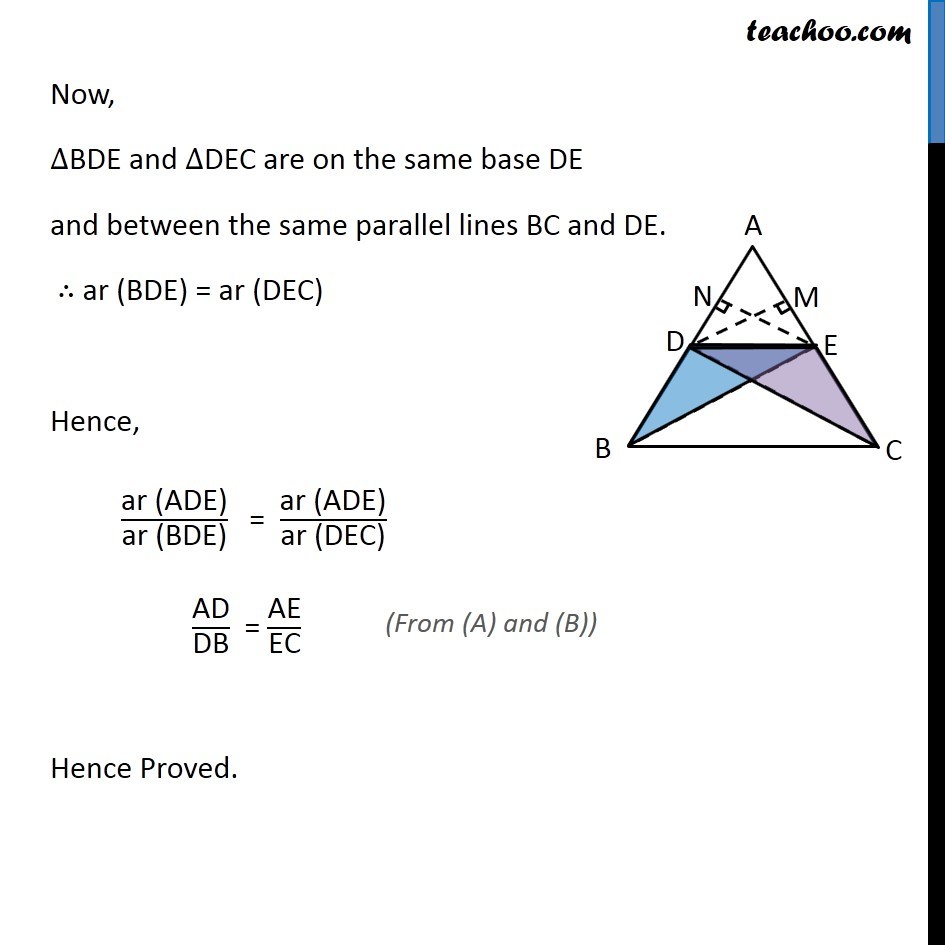
Theorem 6.1: If a line is drawn parallel to one side of a triangle to intersect the other two side in distinct points, the other two sides are divided in the same ratio. Given: Δ ABC where DE ∥ BC To Prove: 𝐴𝐷/𝐷𝐵 = 𝐴𝐸/𝐸𝐶 Construction: Join BE and CD Draw DM ⊥ AC and EN ⊥ AB. Proof: Now, Now, ar (ADE) = 1/2 × Base × Height = 1/2 × AE × DM ar (DEC) = 1/2 × Base × Height = 1/2 × EC × DM Divide (3) and (4) "ar (ADE)" /"ar (DEC)" = (1/2 " × AE × DM" )/(1/2 " × EC × DM " ) "ar (ADE)" /"ar (DEC)" = "AE" /"EC" Now, ∆BDE and ∆DEC are on the same base DE and between the same parallel lines BC and DE. ∴ ar (BDE) = ar (DEC) Hence, "ar (ADE)" /"ar (BDE)" = "ar (ADE)" /"ar (DEC)" "AD" /"DB" = "AE" /"EC" Hence Proved.