Question 1 - Forming equations graphically and algebraically - Chapter 3 Class 10 Pair of Linear Equations in Two Variables

Transcript

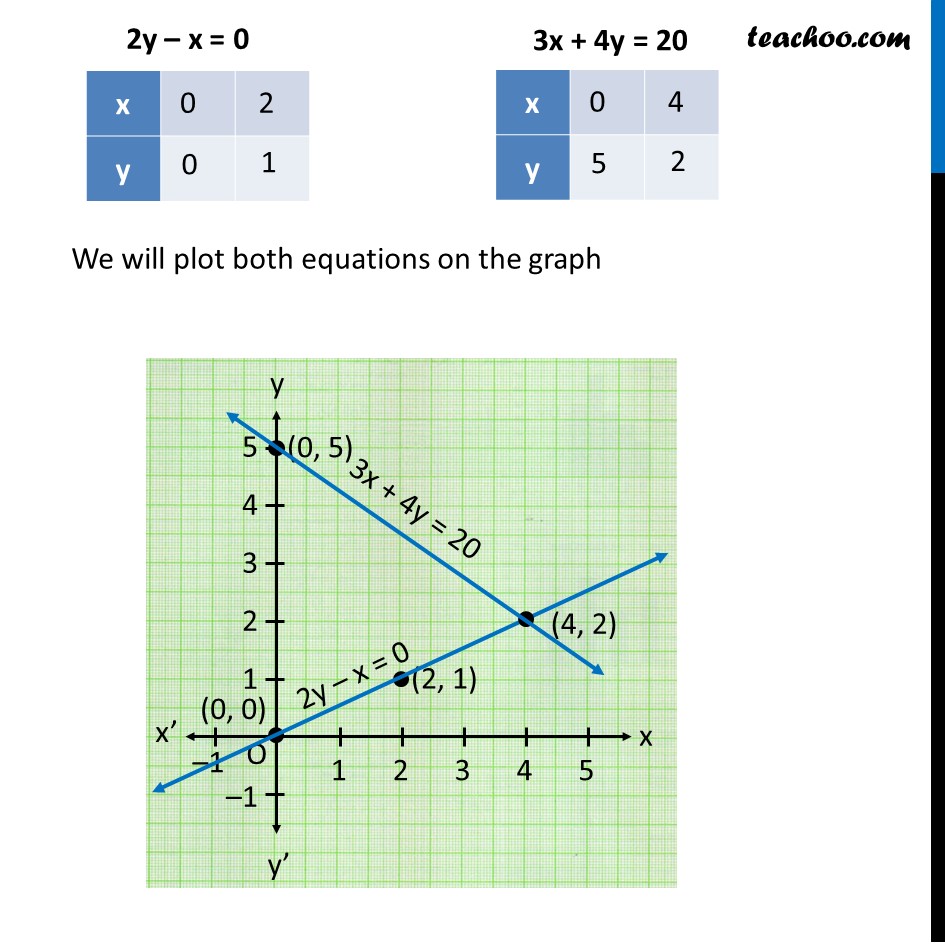
Question 1 Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play Hoopla (a game in which you throw a ring on the items kept in a stall, and if the ring covers any object completely, you get it). The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. If each ride costs Rs 3, and a game of Hoopla costs Rs 4, how would you find out the number of rides she had and how many times she played Hoopla, provided she spent Rs 20. Represent the situation algebraically and graphically. Let the number of rides Akhila has on the giant wheel be x. Let the number of times Akhila played Hoopla be y. Given that The number of times she played Hoopla is half the number of rides she had on the Giant Wheel y = 1/2 x 2y = x 2y – x = 0 Also, If each ride costs Rs 3, and a game of Hoopla costs Rs 4, how would you find out the number of rides she had and how many times she played Hoopla, provided she spent Rs 20 Number of rides of giant wheel × (Rs 3) + Number of times Hoopla played × (Rs 4) = Total money 3x + 4y = 20 Now, plotting equations 2y – x = 0 ...(1) 3x + 4y = 20 …(2) For Equation (1) 2y – x = 0 Let x = 0 2y − 0 = 0 2y = 0 y = 0 So, x = 0, y = 0 is a solution i.e. (0, 0) is a solution Let x = 2 2y − 2 = 0 2y = 2 y = 1 So, x = 2, y = 1 is a solution i.e. (2, 1) is a solution For Equation (2) 3x + 4y = 20 Putting x = 0 3(0) + 4y = 20 0 + 4y = 20 4y = 20 y = 20/4 y = 5 So, x = 0, y = 5 is a solution i.e. (0, 5) is a solution Putting x = 4 3(4) + 4y = 20 12 + 4y = 20 4y = 20 − 12 y = 8/4 y = 2 So, x = 4, y = 2 is a solution i.e. (4, 2) is a solution We will plot both equations on the graph