Ex 8.2, 3 - Chapter 8 Class 8 Algebraic Expressions and Identities

Transcript

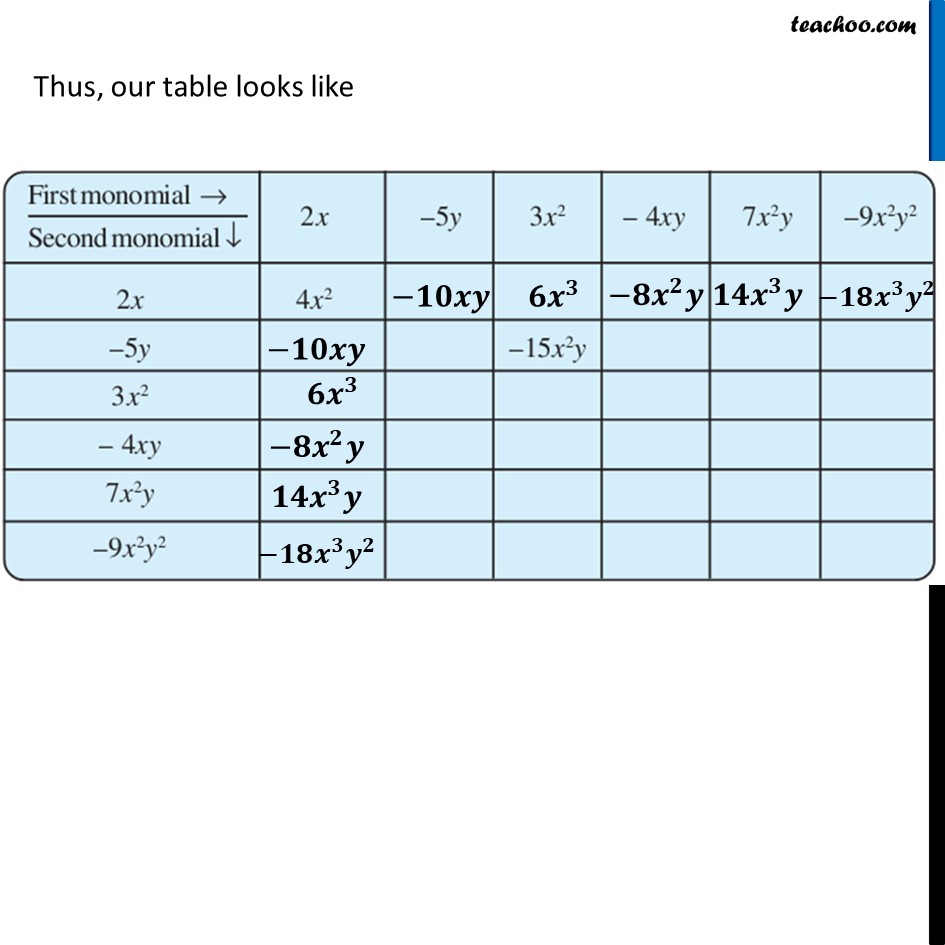
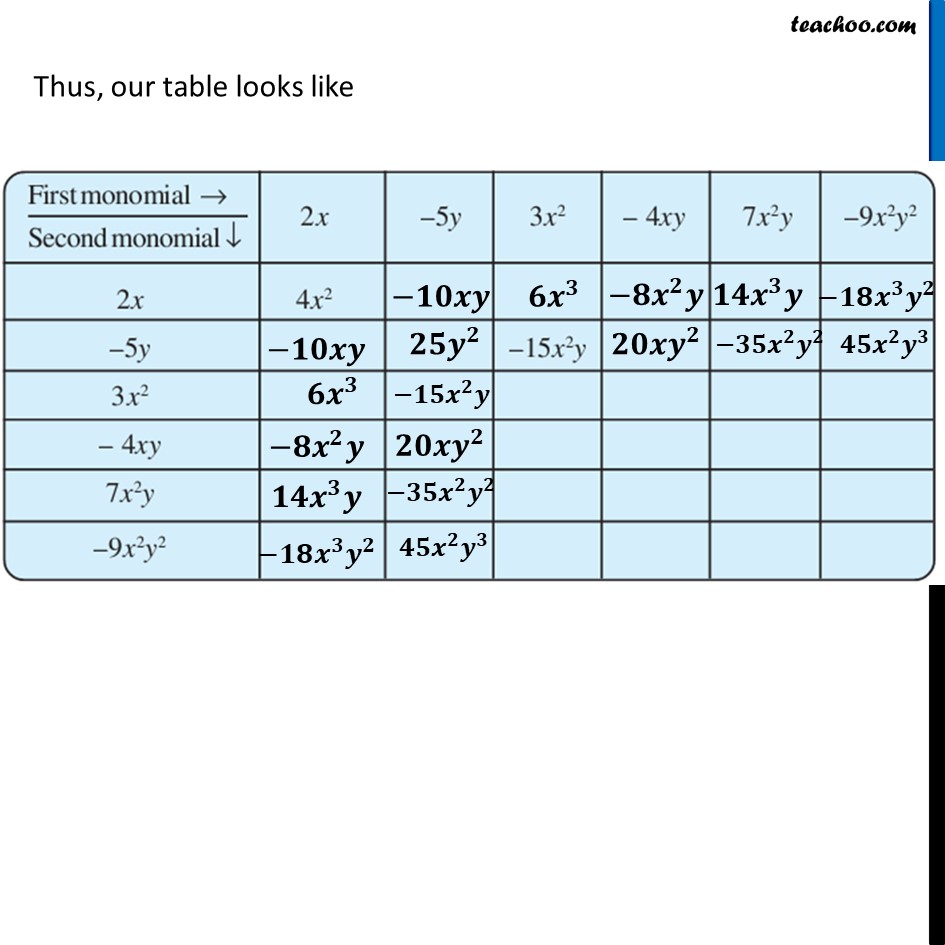
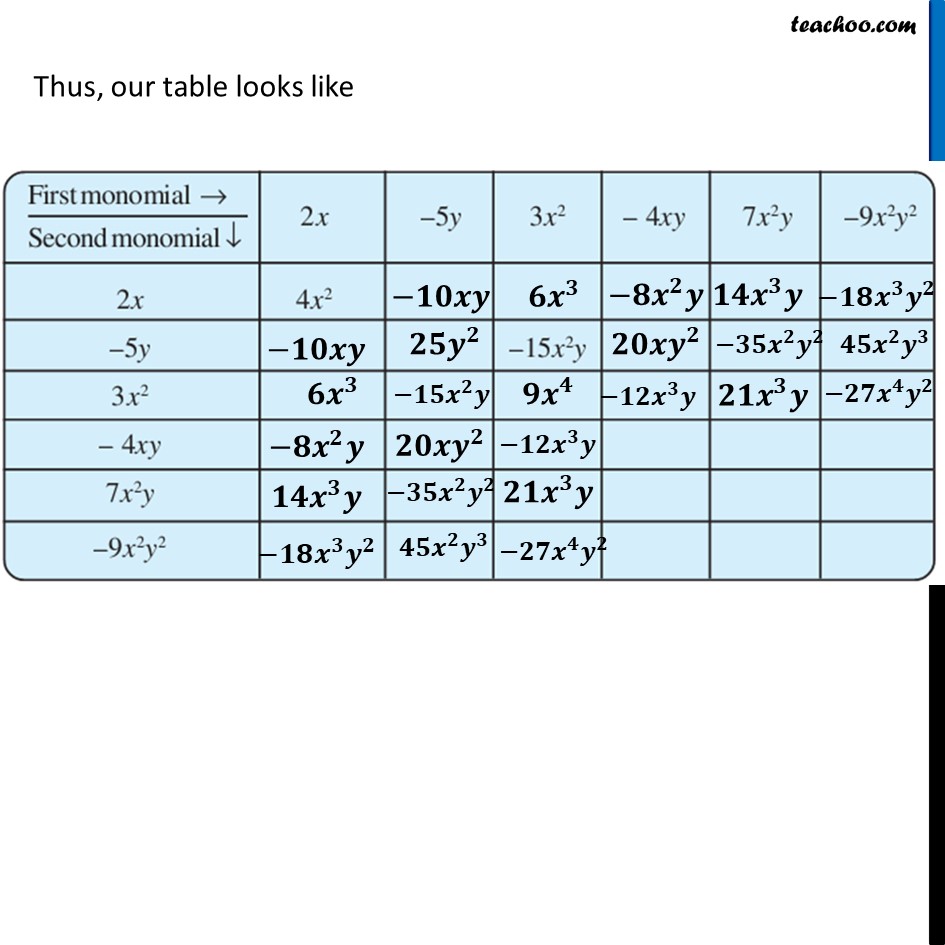
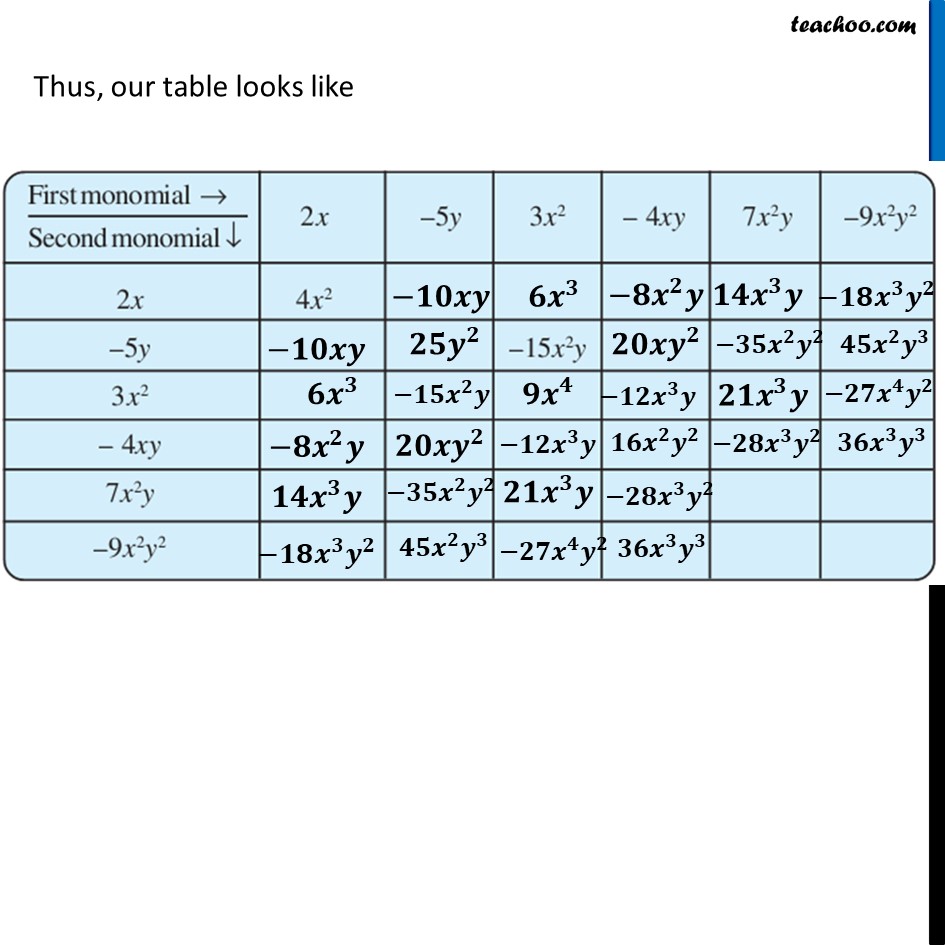
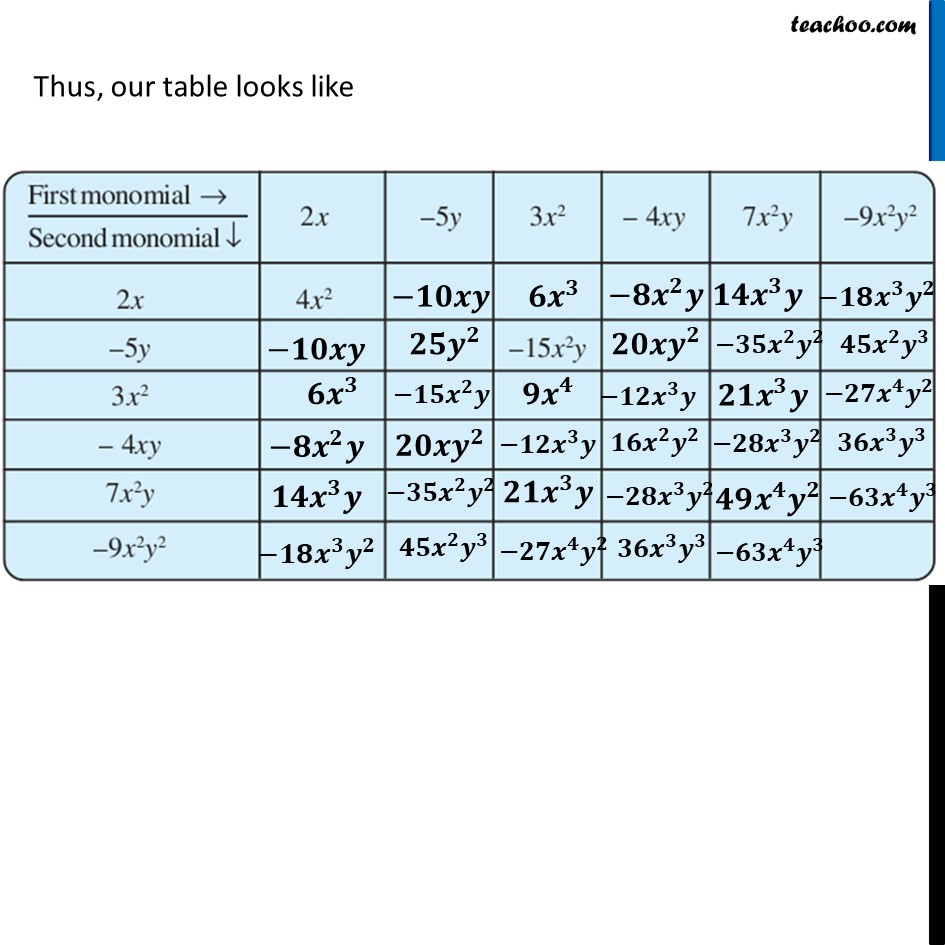
Ex 8.2, 3 Complete the table of products.For 2x 2𝑥 × −5𝑦 = 2 × 𝑥 × −5 × 𝑦 = (2 × −5) × 𝑥 × 𝑦 = −10 × 𝑥 × 𝑦 = −10𝑥𝑦 𝟐𝒙 × 𝟑𝒙^𝟐 = 2 × 𝑥 × 3 × 𝑥^2 = (2 × 3) × (𝑥 × 𝑥^2 ) = 6 × 𝑥^3 = 𝟔𝒙^𝟑 𝟐𝒙 × −𝟒𝒙𝒚 = 2 × 𝑥 × −4 × 𝑥 × y = (2 × −4) × (𝑥 × 𝑥) × 𝑦 = −8 ×〖 𝑥〗^2 × 𝑦 = −𝟖𝒙^𝟐 𝒚 𝟐𝒙 × 𝟕𝒙^𝟐 𝒚 = 2 × 𝑥 × 7 × 𝑥^2 × y = (2 × 7) × (𝑥 × 𝑥^2 ) × 𝑦 = 14 × 𝑥^3 × 𝑦 = 𝟏𝟒𝒙^𝟑 𝒚 𝟐𝒙 × −𝟗𝒙^𝟐 𝒚^𝟐 = 2 × 𝑥 × −9 × 𝑥^2 × y^2 = (2 × −9) × (𝑥 × 𝑥^2 ) × 𝑦^2 = −18 × 𝑥^3 × 𝑦^2 = −𝟏𝟖𝒙^𝟑 𝒚^𝟐 Thus, our table looks like (−𝟓𝒚) × (−𝟓𝒚) = −5 × 𝑦 × −5 × 𝑦 = (−5 × −5) × (𝑦 × 𝑦) = 25 × 𝑦^2 = 𝟐𝟓𝒚^𝟐 (−𝟓𝒚) × (−𝟒𝒙𝒚) = −5 × 𝑦 × −4 × 𝑥 × 𝑦 = (−5 × −4) × 𝑦 × 𝑦 × 𝑥 = 20 × 𝑦^2 × 𝑥 = 𝟐𝟎𝒚^𝟐 𝒙 For −5y (−𝟓𝒚) × 𝟕𝒙^𝟐 𝒚 = −5 × 𝑦 × 7 × 𝑥^2 × 𝑦 = (−5 × 7) × (𝑦 × 𝑦) × 𝑥^2 = −35 × 𝑦^2 × 𝑥^2 = −𝟑𝟓𝒚^𝟐 𝒙^𝟐 (−𝟓𝒚) × (−𝟗𝒙^𝟐 𝒚^𝟐 ) = −5 × 𝑦 × (−9) × 𝑥^2 × 𝑦^2 = (−5 × −9) × 𝑥^2 × (𝑦 × 𝑦^2 ) = 45 × 𝑥^2 × 𝑦^3 = 𝟒𝟓𝒙^𝟐 𝒚^𝟑 Thus, our table looks like For 3x2 𝟑𝒙^𝟐 × 𝟑𝒙^𝟐 = 3 × 𝑥^2 × 3 × 𝑥^2 = (3 × 3) × (𝑥^2 × 𝑥^2 ) = 9 × 𝑥^4 = 𝟗𝒙^𝟒 𝟑𝒙^𝟐 × (−𝟒𝒙𝒚) = 3 × 𝑥^2 × −4 × 𝑥 × 𝑦 = (3 × −4) × (𝑥^2 × 𝑥) × 𝑦 = −12 × 𝑥^3 × 𝑦 = −𝟏𝟐𝒙^𝟑 𝒚 For 3x2 𝟑𝒙^𝟐 × 𝟑𝒙^𝟐 = 3 × 𝑥^2 × 3 × 𝑥^2 = (3 × 3) × (𝑥^2 × 𝑥^2 ) = 9 × 𝑥^4 = 𝟗𝒙^𝟒 𝟑𝒙^𝟐 × (−𝟒𝒙𝒚) = 3 × 𝑥^2 × −4 × 𝑥 × 𝑦 = (3 × −4) × (𝑥^2 × 𝑥) × 𝑦 = −12 × 𝑥^3 × 𝑦 = −𝟏𝟐𝒙^𝟑 𝒚 𝟑𝒙^𝟐 × 𝟕𝒙^𝟐 𝒚 = 3 × 𝑥^2 × 7 × 𝑥^2 × 𝑦 = (3 × 7)×(𝑥^2 × 𝑥^2 ) × 𝑦 = 21 × 𝑥^4 × 𝑦 = 𝟐𝟏𝒙^𝟒 𝒚 𝟑𝒙^𝟐 × (−𝟗𝒙^𝟐 𝒚^𝟐) = 3 × 𝑥^2 × 7 × 𝑥^2 × 𝑦 = (3 × −9) × (𝑥^2 × 𝑥^2 ) × 𝑦^2 = −27 × 𝑥^4 ×𝑦^2 = −𝟐𝟕𝒙^𝟒 𝒚^𝟐 Thus, our table looks like For −4xy (−𝟒𝒙𝒚) × (−𝟒𝒙𝒚) = −4 × 𝑥 × 𝑦 × −4 × 𝑥 × 𝑦 = (−4 × −4) × (𝑥 × 𝑥) × (𝑦 × 𝑦) = 16 × 𝑥^2 × 𝑦^2 = 𝟏𝟔𝒙^𝟐 𝒚^𝟐 (−𝟒𝒙𝒚) × 𝟕𝒙^𝟐 𝒚 = −4 × 𝑥 × 𝑦 × 7 × 𝑥^2 × 𝑦 = (−4 × 7) × (𝑥 × 𝑥^2 ) × (𝑦 × 𝑦) = −28 × 𝑥^3 × 𝑦^2 = −𝟐𝟖𝒙^𝟑 𝒚^𝟐 For −4xy (−𝟒𝒙𝒚) × (−𝟗𝒙^𝟐 𝒚^𝟐 ) = −4 × 𝑥 × 𝑦 × −9 × 𝑥^2 × 𝑦^2 = (−4 × −9) × (𝑥 × 𝑥^2 ) × (𝑦 × 𝑦^2 ) = 36 × 𝑥^3 × 𝑦^3 = 𝟑𝟔𝒙^𝟑 𝒚^𝟑 Thus, our table looks like (𝟕𝒙^𝟐 𝒚) × (𝟕𝒙^𝟐 𝒚) = 7 × 𝑥^2 × 𝑦 × 7 × 𝑥^2 × 𝑦 = (7 × 7) × (𝑥^2 × 𝑥^2 ) × (𝑦 × 𝑦) = 49 × 𝑥^4 × 𝑦^2 = 𝟒𝟗𝒙^𝟒 𝒚^𝟐 (𝟕𝒙^𝟐 𝒚) × (−𝟗𝒙^𝟐 𝒚^𝟐 ) = 7 × 𝑥^2 × 𝑦 × −9 × 𝑥^2 × 𝑦^2 = (7 × −9) × (𝑥^2 × 𝑥^2 ) × (𝑦 × 𝑦^2 ) = −63 × 𝑥^4 × 𝑦^3 = −𝟔𝟑𝒙^𝟒 𝒚^𝟑 (−𝟗𝒙^𝟐 𝒚^𝟐 ) × (−𝟗𝒙^𝟐 𝒚^𝟐 ) = −9 × 𝑥^2 × 𝑦^2 × −9 × 𝑥^2 × 𝑦^2 = (−9 × −9) × (𝑥^2 × 𝑥^2 ) × (𝑦^2 × 𝑦^2 ) = 81 × 𝑥^4 × 𝑦^4 = 𝟖𝟏𝒙^𝟒 𝒚^𝟒