Ex 9.2, 10 - Chapter 9 Class 7 Perimeter and Area

Transcript

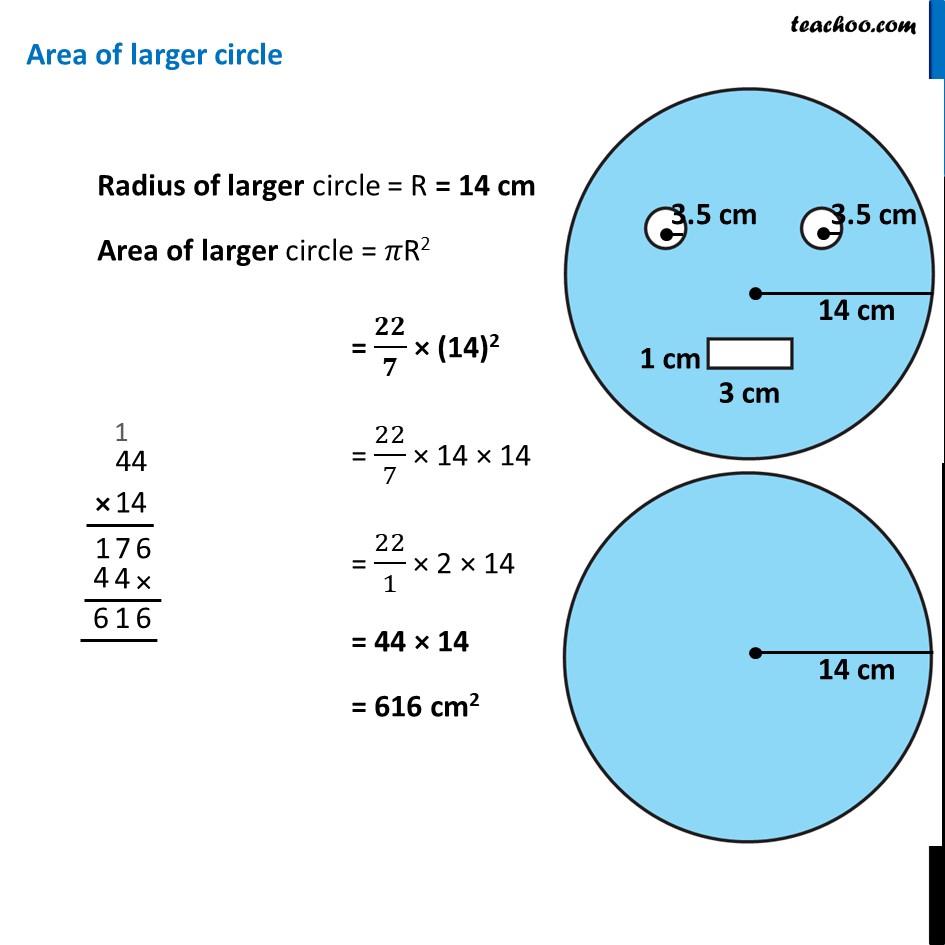
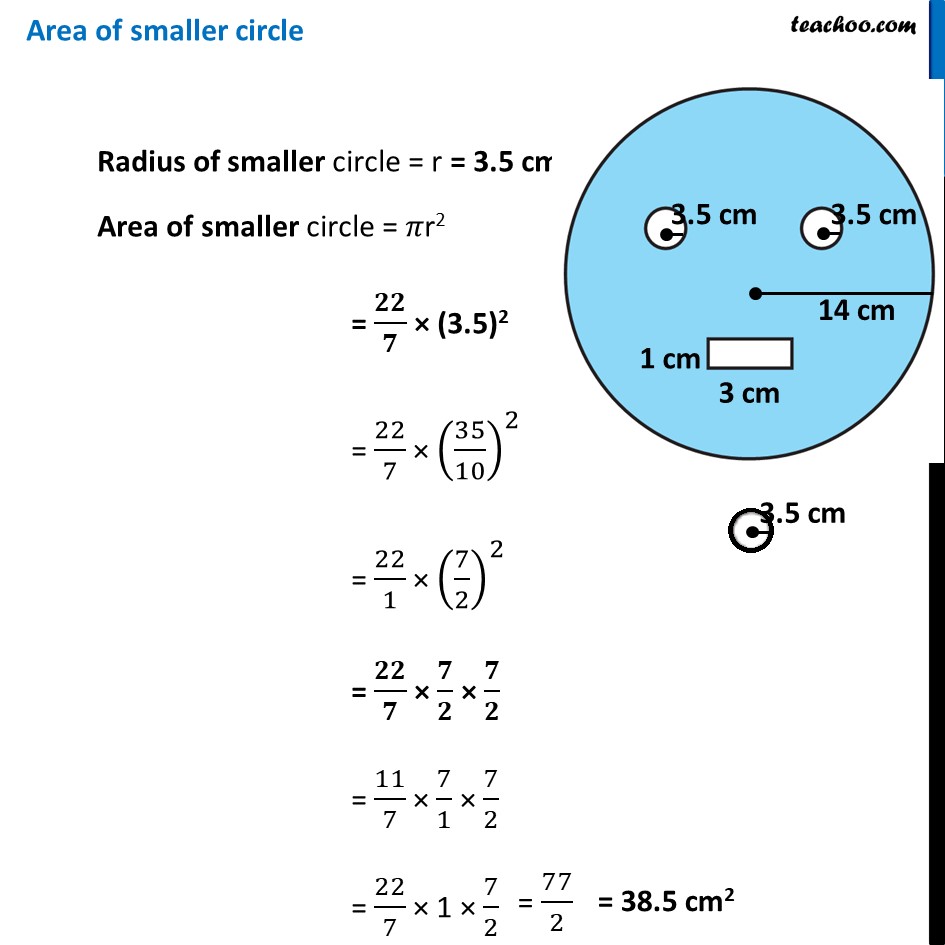
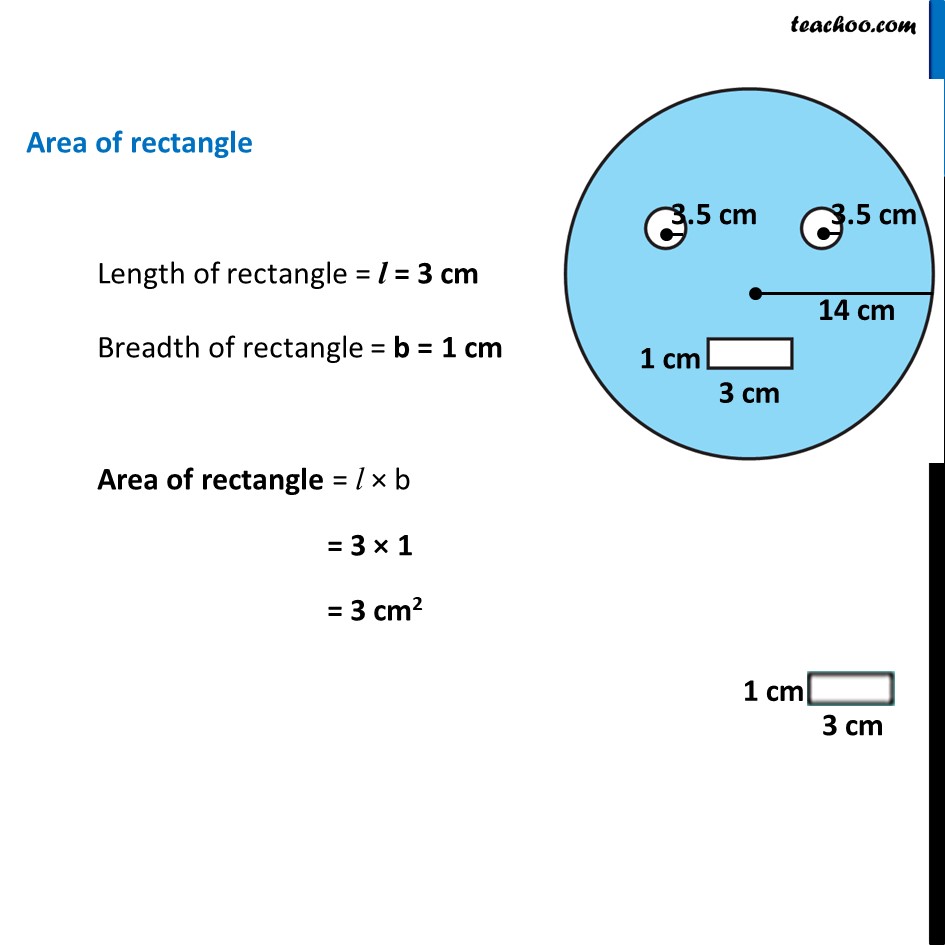
Ex 9.2, 10 From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1cm are removed. (as shown in the adjoining figure). Find the area of the remaining sheet. (𝑇𝑎𝑘𝑒 𝜋=22/7) Remaining Area = Area of larger circle − 2 × Area of smaller circle − Area of rectangle Area of larger circle Radius of larger circle = R = 14 cm Area of larger circle = 𝜋R2 = 𝟐𝟐/𝟕 × (14)2 = 22/7 × 14 × 14 = 22/1 × 2 × 14 = 44 × 14 = 616 cm2 Area of smaller circle Radius of smaller circle = r = 3.5 cm Area of smaller circle = 𝜋r2 = 𝟐𝟐/𝟕 × (3.5)2 = 22/7 × (35/10)^2 = 22/1 × (7/2)^2 = 𝟐𝟐/𝟕 × 𝟕/𝟐 × 𝟕/𝟐 = 11/7 × 7/1 × 7/2 = 22/7 × 1 × 7/2 Area of rectangle Length of rectangle = l = 3 cm Breadth of rectangle = b = 1 cm Area of rectangle = l × b = 3 × 1 = 3 cm2 Therefore, ∴ Remaining Area = Area of larger circle − 2 × Area of smaller circle − Area of rectangle = 616 − 2 × (𝟕𝟕/𝟐) − 3 = 616 − 77 − 3 = 616 − 80 = 536 cm2 ∴ Required area is 536 cm2