

Ex 5.1
Last updated at Dec. 16, 2024 by Teachoo



Transcript
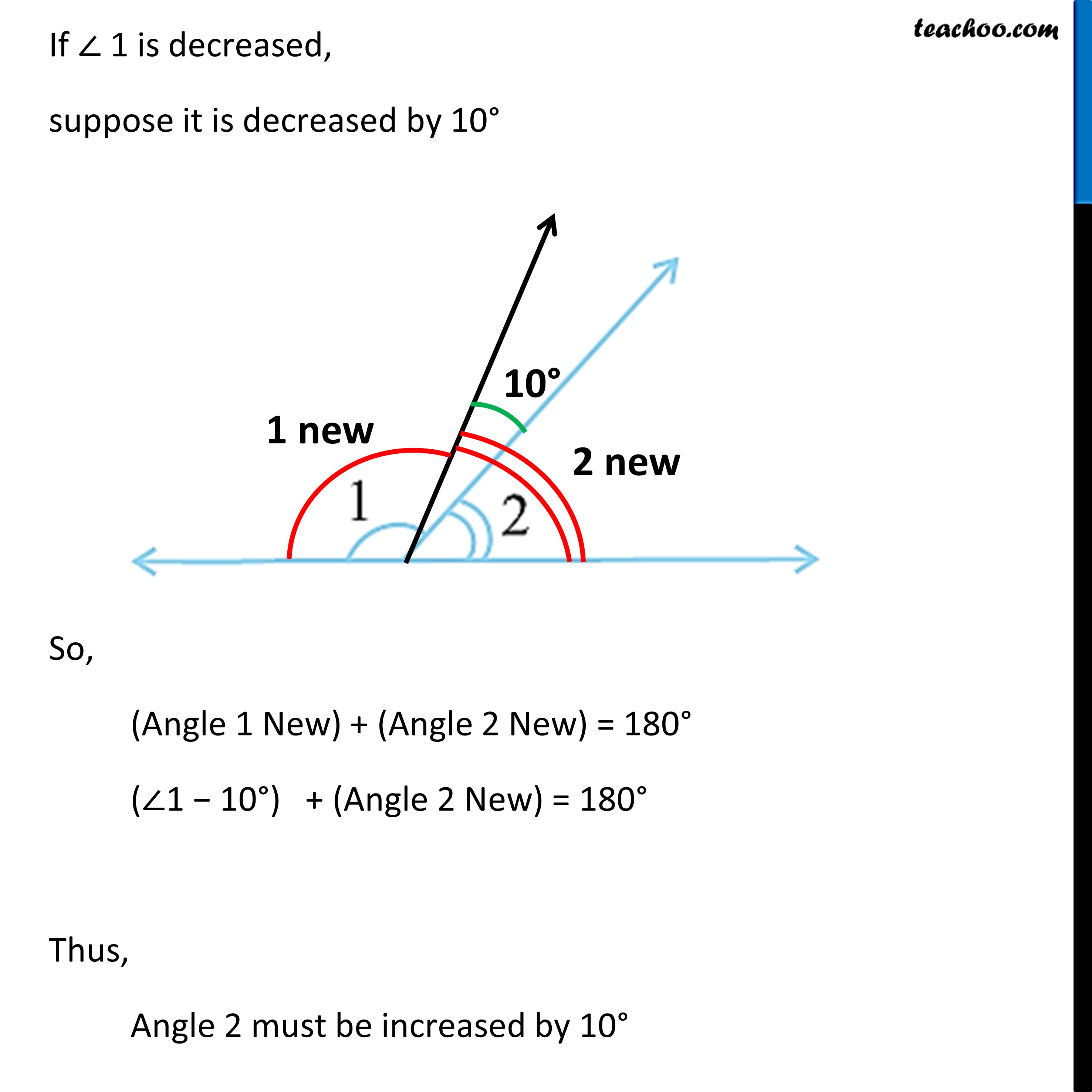
Ex 5.1, 6 (Method 1) In the given figure, ∠1 and ∠2 are supplementary angles. If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.Given, ∠1 and ∠2 are supplementary angles, We know that, If two angles are supplementary, their sum is 180° So, ∠1 + ∠2 = 180° → ∠1 = 180° − ∠2 Now, If ∠1 is decreased by x, ∠1 becomes (∠1 − x). And ∠2 is changed to ∠3, such that (∠1 − x) and ∠3 are also supplementary angles. Then, (∠1 − x) + ∠3 = 180° 180° − ∠2 − x + ∠3 = 180° ∠3 = 180° − 180° + ∠2 + x ∠3 = ∠2 + x So, if ∠ 1 is decreased by x ∠ 2 should be increased by x Hence, in order to make ∠1 and ∠2 supplementary, ∠2 will have to be increased by the same value as ∠1 was decreased. Ex 5.1, 6 (Method 2) In the given figure, ∠1 and ∠2 are supplementary angles. If ∠1 is decreased, what changes should take place in ∠2 so that both the angles still remain supplementary.Given, ∠1 and ∠2 are supplementary, So, ∠1 + ∠2 = 180° If ∠ 1 is decreased, suppose it is decreased by 10° So, (Angle 1 New) + (Angle 2 New) = 180° (∠1 − 10°) + (Angle 2 New) = 180° Thus, Angle 2 must be increased by 10° Our sum becomes (∠1 − 10°) + (∠2 + 10°) = 180° ∠1 + ∠2 + 10° − 10° = 180° ∠1 + ∠2 = 180° Suppose ∠1 is decreased by 20° So, ∠2 must be increased by 20° Our sum becomes (∠1 − 20°) + (∠2 − 20°) = 180° ∠1 + ∠2 + 20° − 20° = 180° ∠1 + ∠2 = 180° ∴ ∠2 must be increased by the same value as ∠1 is being decreased.