

Constructing tangents to a circle
Question 2 Deleted for CBSE Board 2024 Exams
Question 3 Deleted for CBSE Board 2024 Exams
Question 4 Important Deleted for CBSE Board 2024 Exams
Question 5 Deleted for CBSE Board 2024 Exams
Question 6 Important Deleted for CBSE Board 2024 Exams You are here
Question 7 Important Deleted for CBSE Board 2024 Exams
Constructing tangents to a circle
Last updated at April 16, 2024 by Teachoo







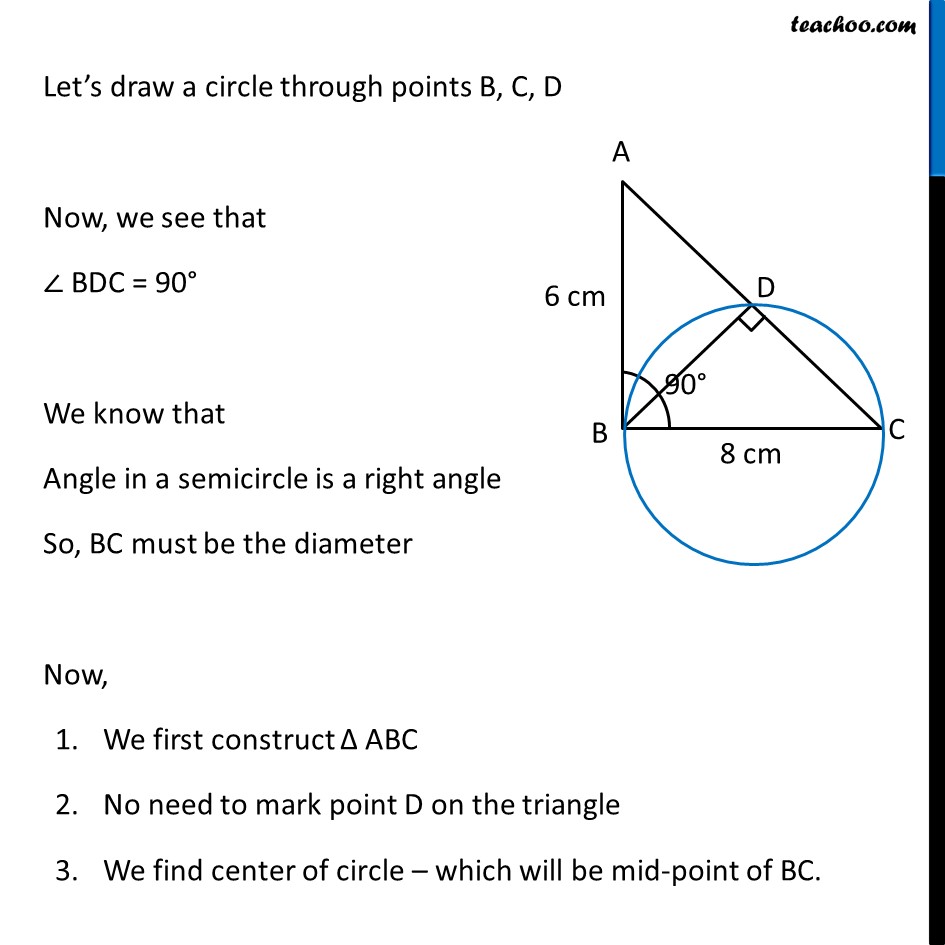
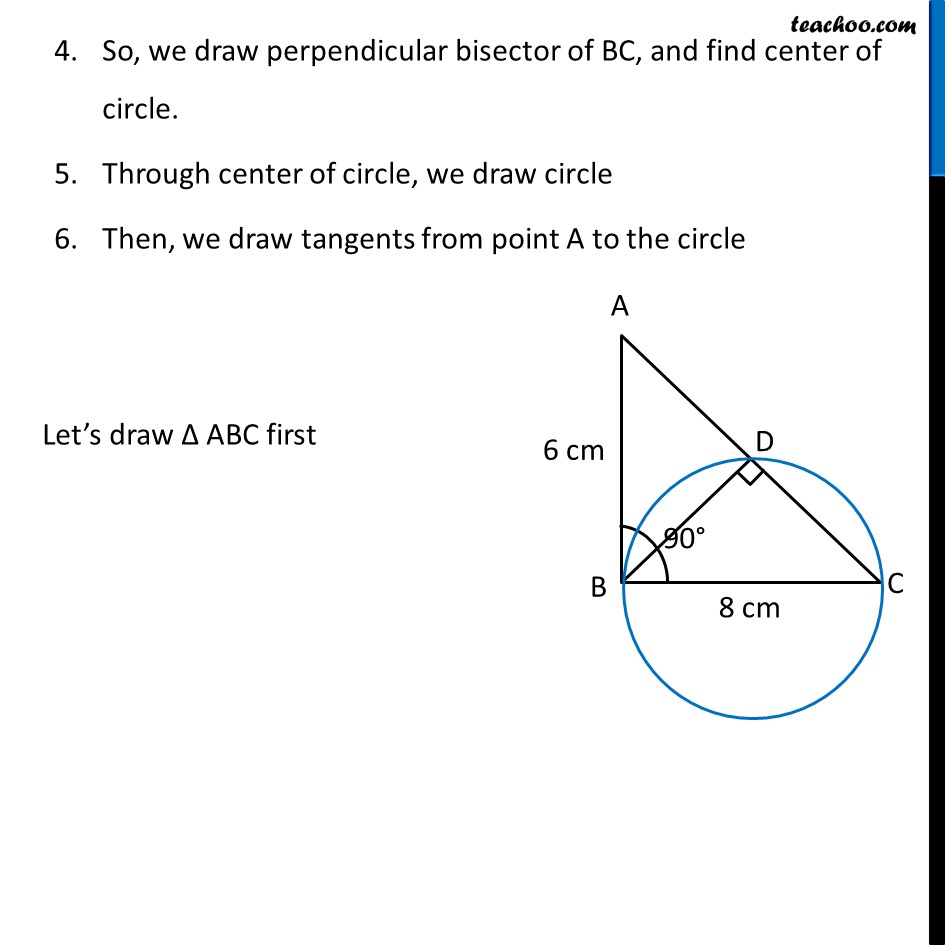
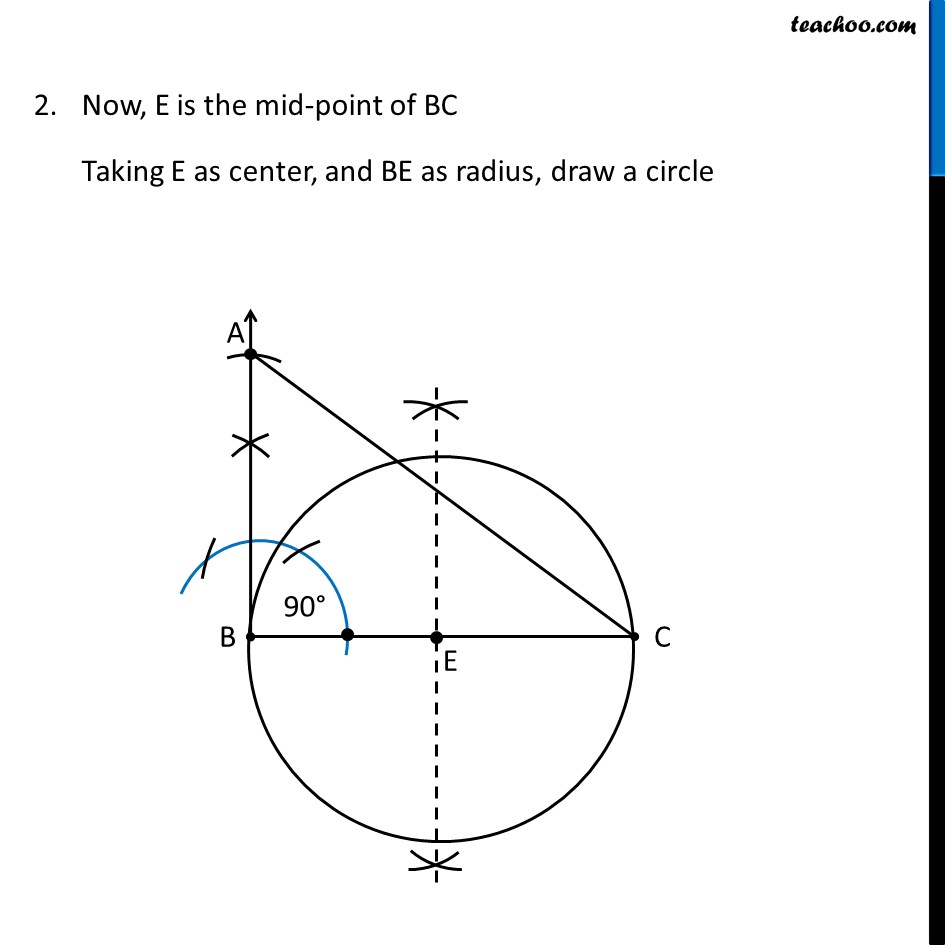
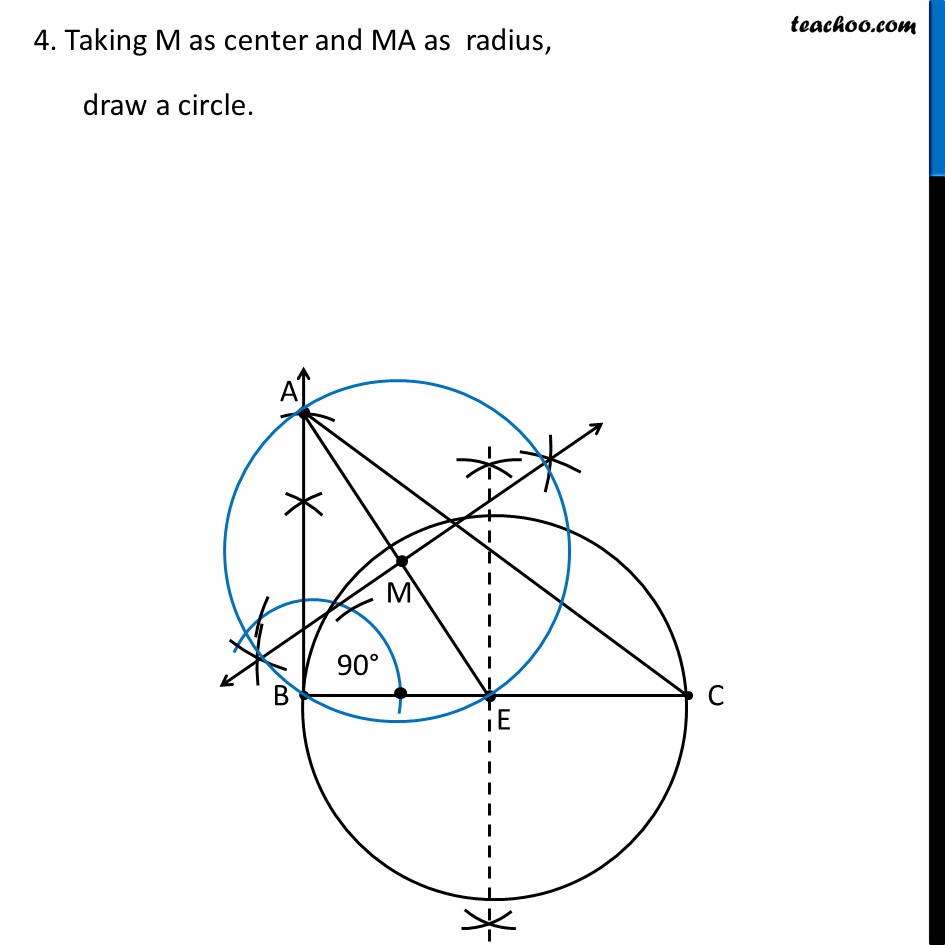
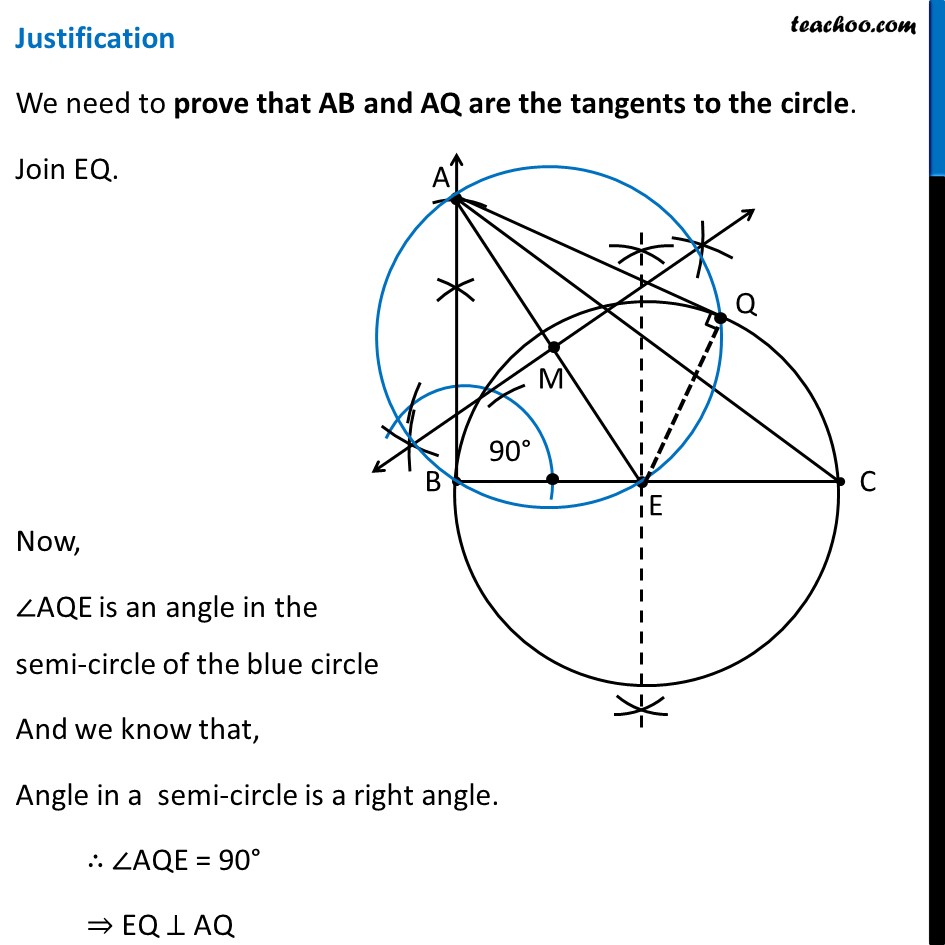
Question 6 Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠ B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle. First we draw a rough sketch Δ ABC Now, it is given that circle is drawn through point B, C, D Let’s draw a circle through points B, C, D Now, we see that ∠ BDC = 90° We know that Angle in a semicircle is a right angle So, BC must be the diameter Now, We first construct Δ ABC No need to mark point D on the triangle We find center of circle – which will be mid-point of BC. So, we draw perpendicular bisector of BC, and find center of circle. Through center of circle, we draw circle Then, we draw tangents from point A to the circle Let’s draw Δ ABC first Steps to draw Δ ABC Draw base BC of side 8 cm Draw ∠ B = 90° 3. Taking B as center, 6 cm as radius, we draw an arc Let the point where arc intersects the ray be point A 4. Join AC ∴ Δ ABC is the required triangle Now, let’s draw a circle and construct tangents Steps to draw circle and tangents Draw perpendicular bisector of line BC Let the line intersect BC at point E. Now, E is the mid-point of BC Taking E as center, and BE as radius, draw a circle We need to construct tangents from point A to the circle Join point A to center of Circle E. Make perpendicular bisector of AE Let M be the midpoint of AE 4. Taking M as center and MA as radius, draw a circle. 5. Let blue circle intersect the other circle at B and Q Join AQ Thus, AB and AQ are the required tangents Justification We need to prove that AB and AQ are the tangents to the circle. Join EQ. Now, ∠AQE is an angle in the semi-circle of the blue circle And we know that, Angle in a semi-circle is a right angle. ∴ ∠AQE = 90° ⇒ EQ ⊥ AQ Since EQ is the radius of the circle, AQ has to be a tangent of the circle. Similarly, AB is a tangent of the circle.