

Linear equations given - Unbounded
Linear equations given - Unbounded
Last updated at Dec. 16, 2024 by Teachoo




Transcript
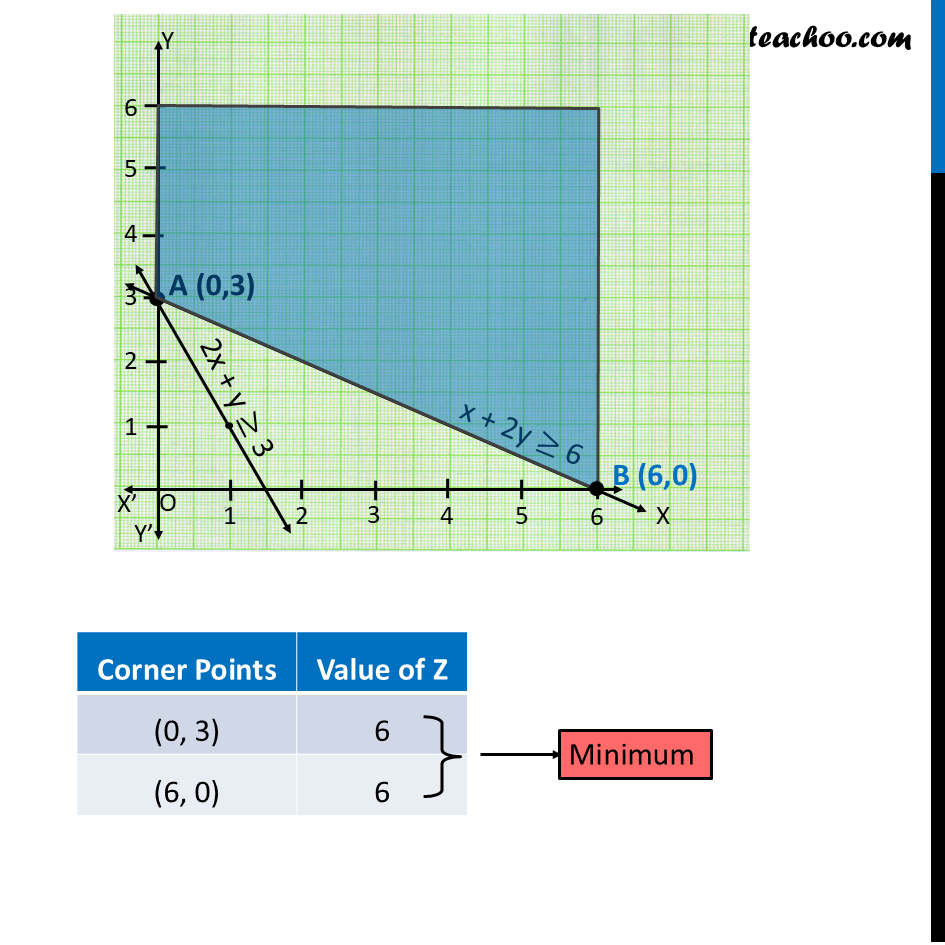
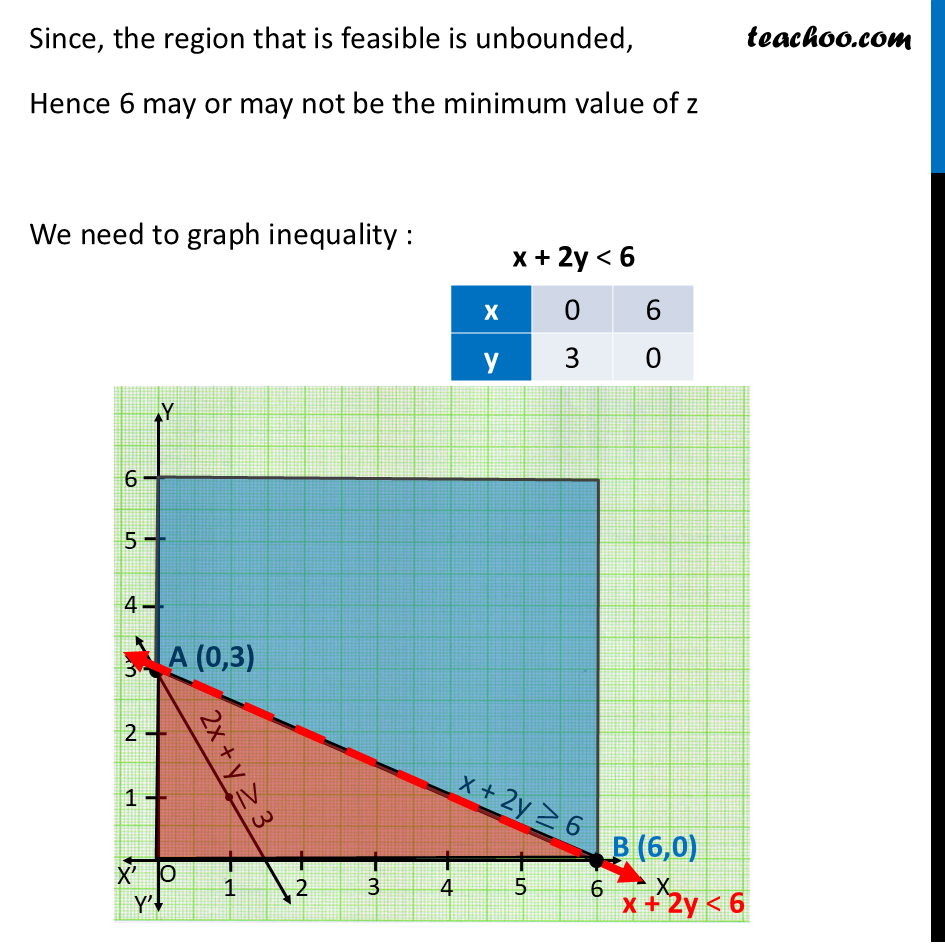
Ex 12.1, 6 Solve the following Linear Programming Problems graphically: Minimise Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0. Show that the minimum of Z occurs at more than two points. Minimize Z = x + 2y Subject to 2x + y ≥ 3 x + 2y ≥ 6 x , y ≥ 0 2x + y ≥ 3 x + 2y ≥ 6 Since, the region that is feasible is unbounded, Hence 6 may or may not be the minimum value of z We need to graph inequality : There is no common point between feasible region & inequality ∴ Z = 6 is minimum on all points joining line (0, 3), (6, 0) i.e. Z = 6 will be minimum on x + 2y = 6 Explanation – Taking points on line x +2y = 6 Hence, Z is minimum at all the points joining (0, 3) & (6, 0) ⇒ Z will be minimum on all points joining line (0, 3) & (6, 0) ∴ Z will be minimum on x + 2y = 6