Misc 2 - Chapter 12 Class 12 Linear Programming

Transcript

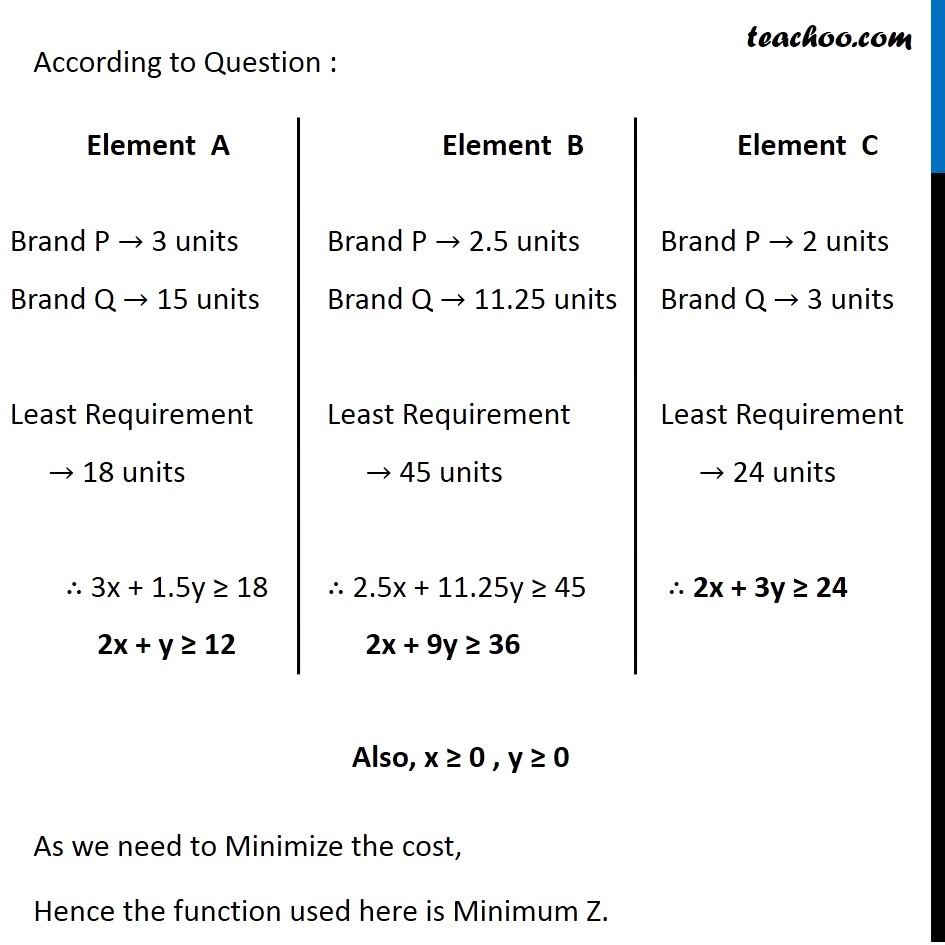
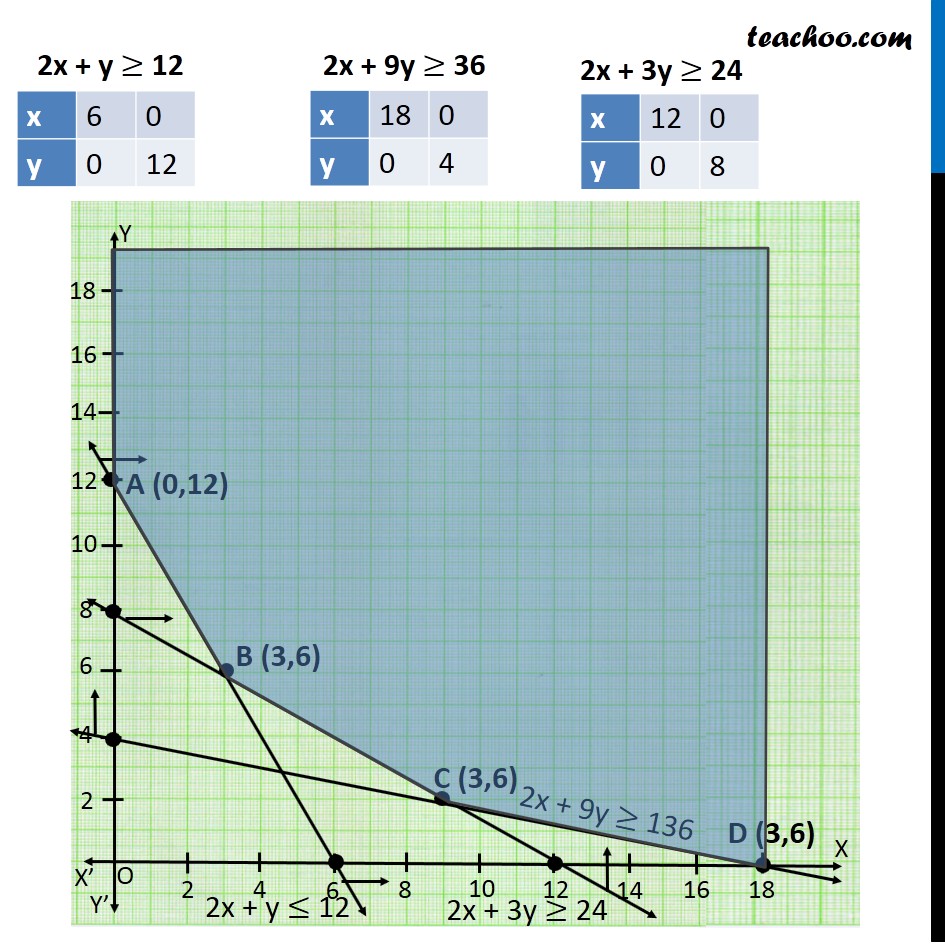
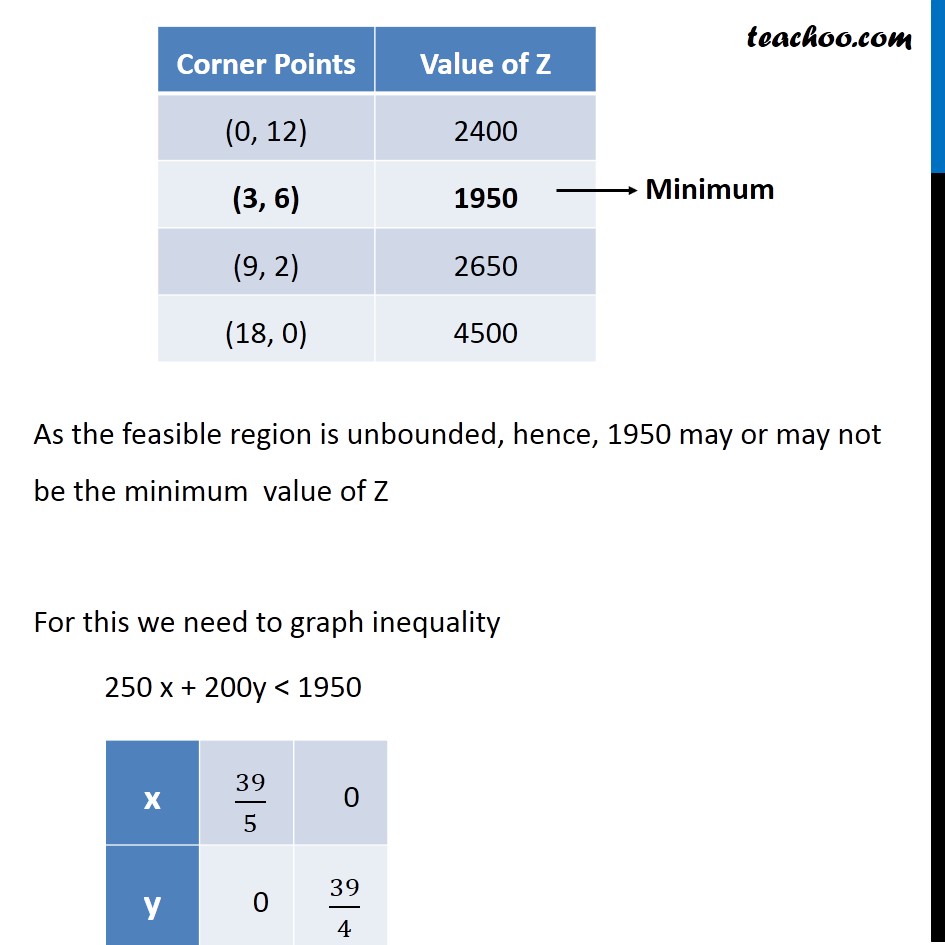
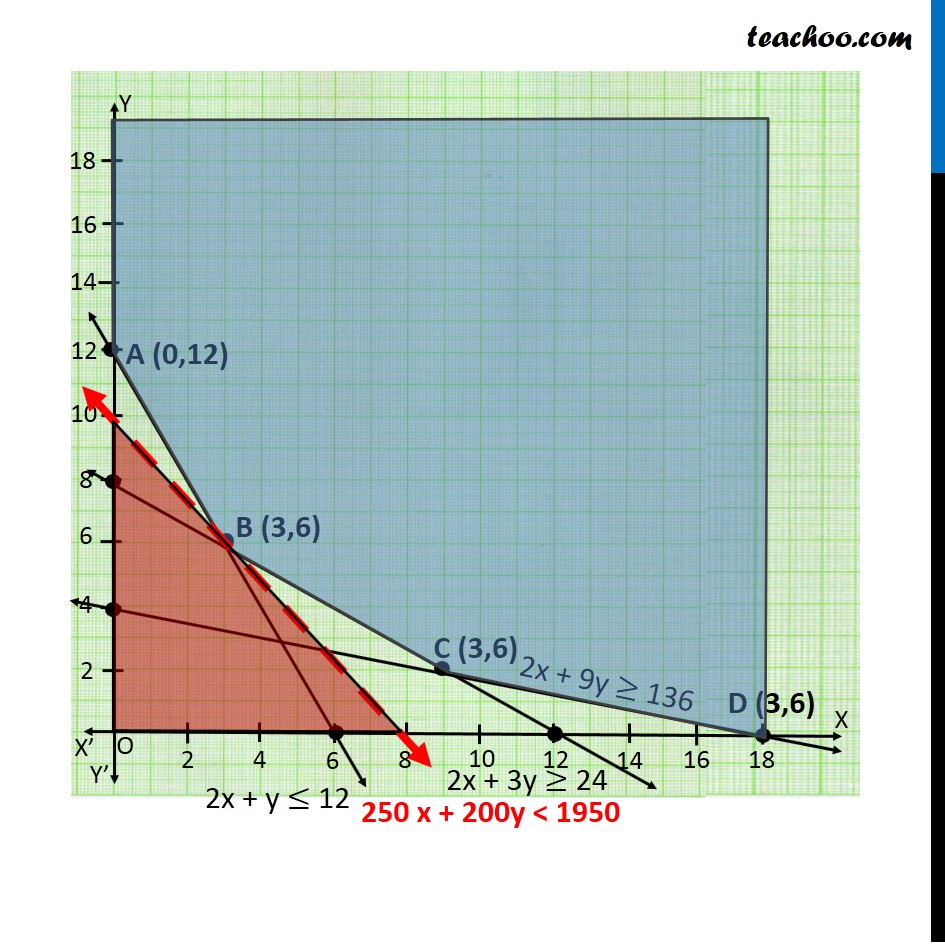
Misc 2 A farmer mixes two brands P and Q of cattle feed. Brand P, costing Rs 250 per bag, contains 3 units of nutritional element A, 2.5 units of element B and 2 units of element C. Brand Q costing Rs 200 per bag contains 1.5 units of nutritional element A, 11.25 units of element B, and 3 units of element C. The minimum requirements of nutrients A, B and C are 18 units, 45 units and 24 units respectively. Determine the number of bags of each brand which should be mixed in order to produce a mixture having a minimum cost per bag? What is the minimum cost of the mixture per bag? Let the mixture contain x bags of brand P & y bags of brand Q According to Question : As we need to Minimize the cost, Hence the function used here is Minimum Z. Element A Brand P → 3 units Brand Q → 15 units Least Requirement → 18 units ∴ 3x + 1.5y ≥ 18 2x + y ≥ 12 Element B Brand P → 2.5 units Brand Q → 11.25 units Least Requirement → 45 units ∴ 2.5x + 11.25y ≥ 45 2x + 9y ≥ 36 Element C Brand P → 2 units Brand Q → 3 units Least Requirement → 24 units ∴ 2x + 3y ≥ 24 Now, Cost of brand P → Rs 250 Cost of brand Q → Rs 200 ∴ Minimize Z = 250 x + 200 y Combining all constraints : Min z = 250 x + 200 y Subject to constraints 2x + y ≥ 12 2x + 9y ≥ 36 2x + 3y ≥ 24 x ≥ 0, y ≥ 0 As the feasible region is unbounded, hence, 1950 may or may not be the minimum value of Z For this we need to graph inequality 250 x + 200y < 1950 Since there is no common point between the feasible region f the inequality. Hence, the cost will be minimum if The mixture contains = 3 bags of brand P mixture contains = 6 bags of brand Q Minimum cost is Rs 1950