Ex 13.3, 3 - Chapter 13 Class 12 Probability (Term 2)
Last updated at May 29, 2018 by Teachoo
Bayes theorem
Example 16
Ex 13.3, 2 Important
Ex 13.3, 3 You are here
Misc 3
Ex 13.3, 4 Important
Ex 13.3, 9
Ex 13.3, 5
Ex 13.3, 13 (MCQ) Important
Example 21 Important
Ex 13.3, 6 Important
Ex 13.3, 10 Important
Example 18 Important
Example 17 Important
Ex 13.3, 7
Ex 13.3, 8 Important
Example 19 Important
Ex 13.3, 11
Ex 13.3, 12 Important
Example 37 Important
Example 20 Important
Example 33 Important
Misc 12
Misc 16 Important
Misc 13 Important
Chapter 13 Class 12 Probability (Term 2)
Concept wise
- Conditional Probability - Values given
- Conditional Probability - Statement
- Multiplication rule of probability
- Independent events
- Basic Probability
- Theorem of total probability
-
Bayes theorem
- Random Variable - Defination
- Probability distribution
- Mean or Expectation of random variable
- Variance and Standard Deviation of a Random Variable
- Bernoulli Trials
- Binomial Distribution
Transcript
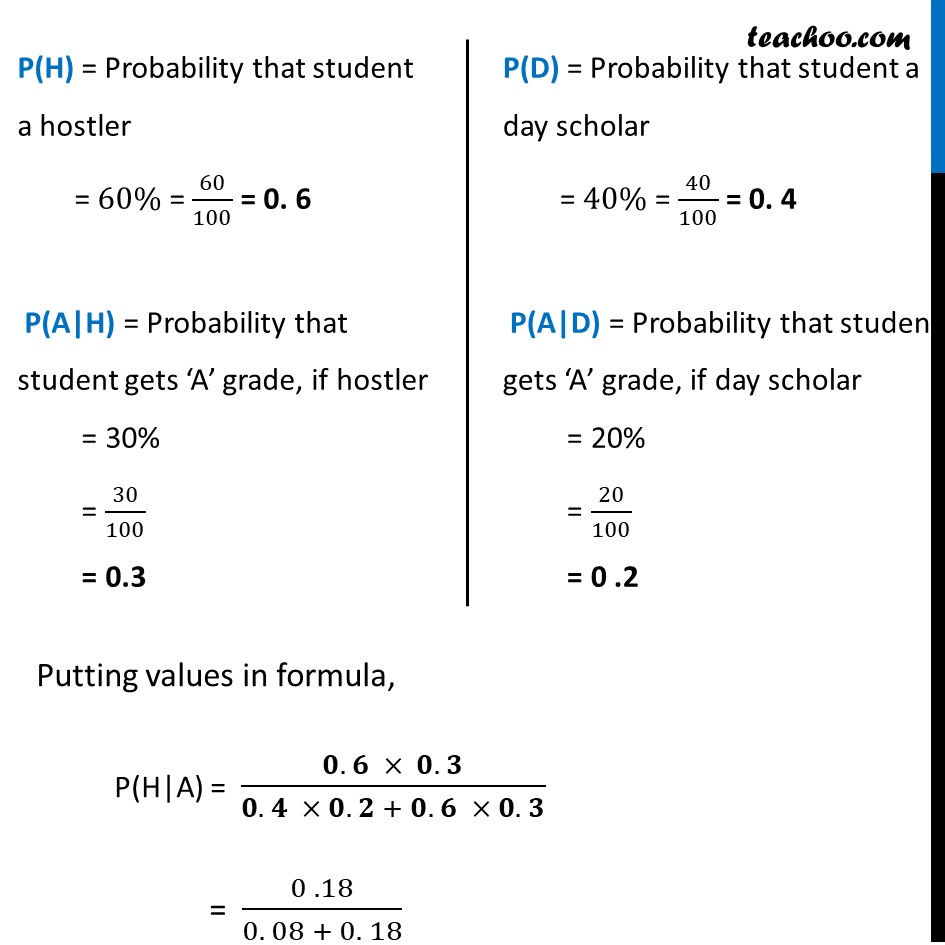
Ex 13.3, 3 Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all students who reside in hostel attain A grade and 20% of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostler? Let H : student selected is a hostler D : student selected is a day scholar A : student has an ‘A’ grade We need to find the Probability that the student selected is a hostler, if he has an ‘A’ grade. i.e. P(H|A) So, P(H|A) = P(H) . P(A|H) P(D) . P(A|D) + P(H) . P(A|H) Putting values in formula, P(H|A) = 0. 6 × 0. 30. 4 × 0. 2 + 0. 6 × 0. 3 = 0 .180. 08 + 0. 18 = 0. 180. 26 = 1826 = 913 Therefore, required probability is 𝟗𝟏𝟑
