Ex 2.2, 12 - Chapter 2 Class 12 Inverse Trigonometric Functions

Transcript

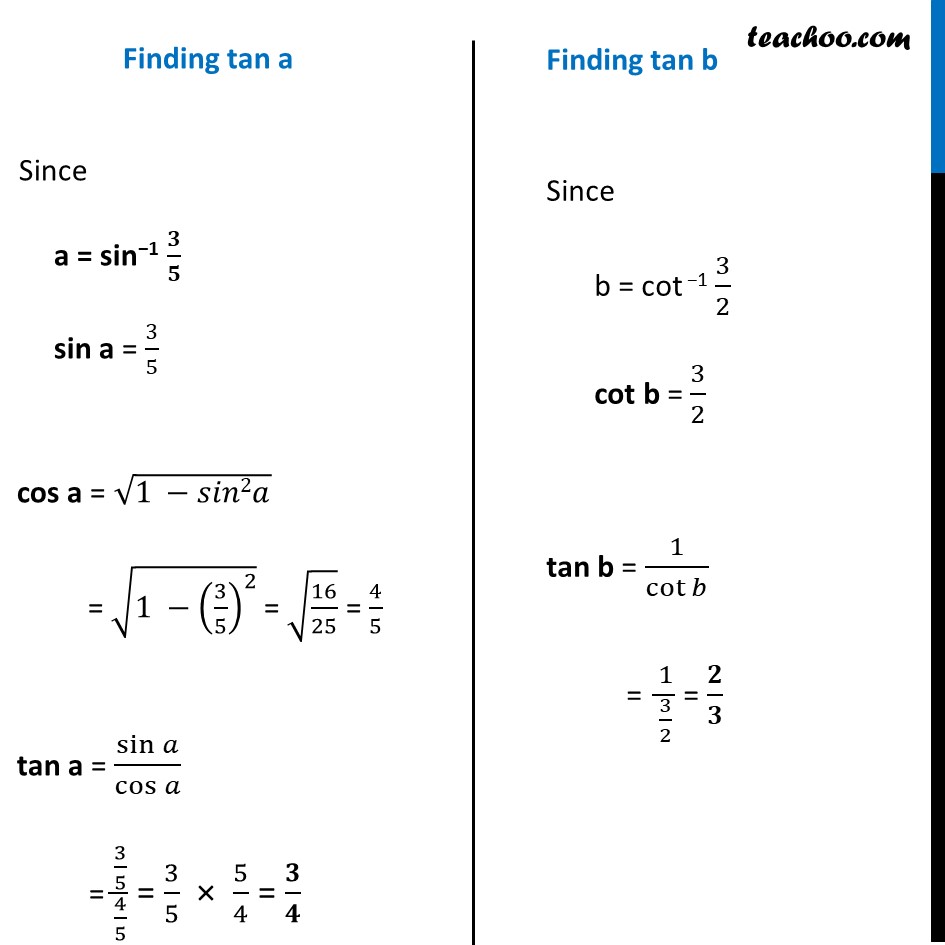
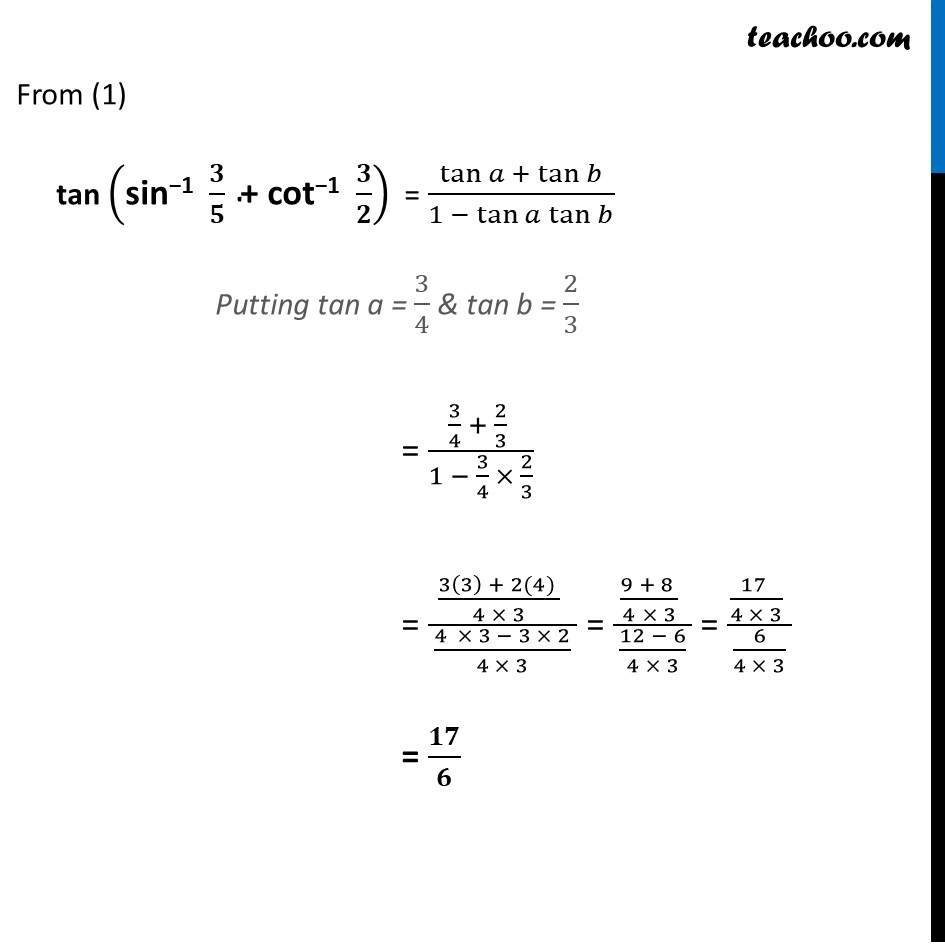
Ex 2.2, 12 tan (sin−1 3/5 + cot−1 3/2 ) We write sin-1 3/5 & cot-1 3/2 in terms of tan-1 Let sin−1 3/5 = a & cot−1 3/2 = b So, our equation becomes tan (sin−1 𝟑/𝟓 + cot−1 𝟑/𝟐 ) = tan (a + b) = 𝒕𝒂𝒏⁡〖𝒂 + 𝒕𝒂𝒏⁡𝒃 〗/(𝟏 − 𝒕𝒂𝒏⁡〖𝒂 𝒕𝒂𝒏⁡𝒃 〗 ) Finding tan a Since a = sin−1 𝟑/𝟓 sin a = 3/5 cos a = √(1 −𝑠𝑖𝑛2𝑎) = √(1 −(3/5)^2 ) = √(16/25) = 4/5 tan a = sin⁡𝑎/cos⁡𝑎 = (3/5)/(4/5) = 3/5 × 5/4 = 𝟑/𝟒 Finding tan b Since b = cot −1 3/2 cot b = 3/2 tan b = 1/cot⁡𝑏 = 1/(3/2) = 𝟐/𝟑 From (1) tan ("sin−1 " 𝟑/𝟓 " + cot−1 " 𝟑/𝟐) = tan⁡〖𝑎 + tan⁡𝑏 〗/(1 − tan⁡〖𝑎 tan⁡𝑏 〗 ) Putting tan a = 3/4 & tan b = 2/3 = (3/4 + 2/3 )/(1 − 3/4 × 2/3) = ((3(3) + 2(4) )/(4 × 3) )/( (4 × 3 − 3 × 2)/(4 × 3) ) = ((9 + 8 )/(4 × 3) )/( (12 − 6)/(4 × 3) ) = ((17 )/(4 × 3) )/( 6/(4 × 3) ) = 𝟏𝟕/𝟔