Are you a bookworm?

Transcript

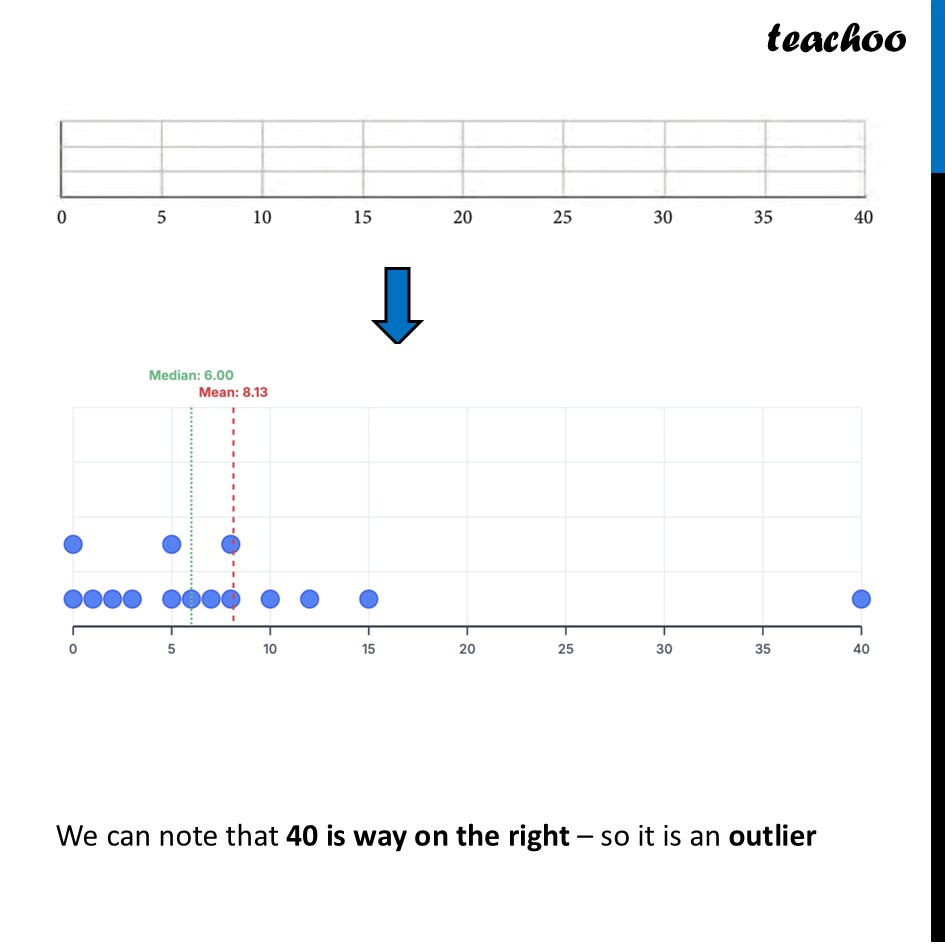
Are you a bookworm?We answer this question After the summer vacation, a class teacher asked his class how many short stories they had read. Each student answered the number of stories read on a piece of paper, as shown below. Find the mean and median number of short stories read. Before calculating them, can you guess whether the mean will be less than or greater than the median? Now, the data is 6, 3, 0, 8, 2, 5, 7, 15, 12, 10, 40, 5, 0, 1, 8 Let’s do our question one-by-one Guess whether the mean will be less than or greater than the median? There is a huge number here: 40. This is a high outlier. It will pull the Mean up. So, the Mean > Median. Mark the data, mean, and median on the dot plot. First, let’s find the mean and median Now, Mean = (𝑆𝑢𝑚 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠)/(𝑁𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛𝑠) = (6 + 3 + 0 + 8 + 2 + 5 + 7 + 15 + 12 + 10 + 40 + 5 + 0 + 1 + 8)/15 = 122/15 = 8.133… For Median We sort the data in ascending order 0, 0, 1, 2, 3, 5, 5, 6, 7, 8, 8, 10, 12, 15, 40 Number of observations = 15 Since number of odd, Median will be the middle number Thus, Median = ((𝟏𝟓 + 𝟏)/𝟐)^𝒕𝒉 observation = (𝟏𝟔/𝟐)^𝒕𝒉 observiation = 8th observation = 6 Thus, we also verified that Mean (8.13) is greater than the Median (6). Marking the data, the mean, and the median on the dot plot below Data: 6, 3, 0, 8, 2, 5, 7, 15, 12, 10, 40, 5, 0, 1, 8 Mean = 8.13 & Median = 6 We can note that 40 is way on the right – so it is an outlier We are asked some more questions like Which of the values would you consider an outlier? In the bookworm data, 40 is the outlier. It is much higher than the rest (where most kids read between 0 and 15 books). Find the mean and median in the absence of the outlier. Remove 40. New Sum =122−40=82. New Count =14. New Mean: 82÷14≈𝟓.𝟖𝟔 New Median: Middle of 5 and 6 =(5 + 6)/2 = 11/2 = 5.5 Notice that The Mean dropped significantly (from 8.13 to 5.86 )! The Median barely changed ( 6 to 5.5).