Question 3 - Figure it out - Page 20, 21 - Chapter 1 Class 7 - Geometric Twins (Ganita Prakash II)

Transcript

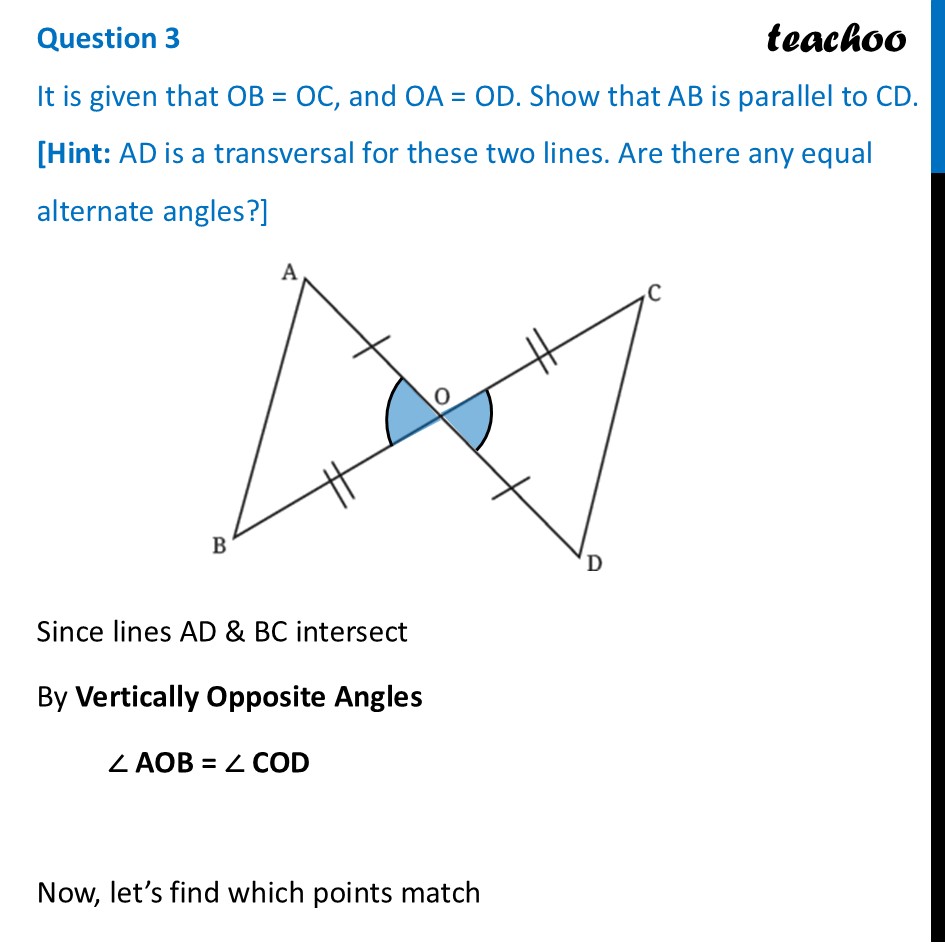
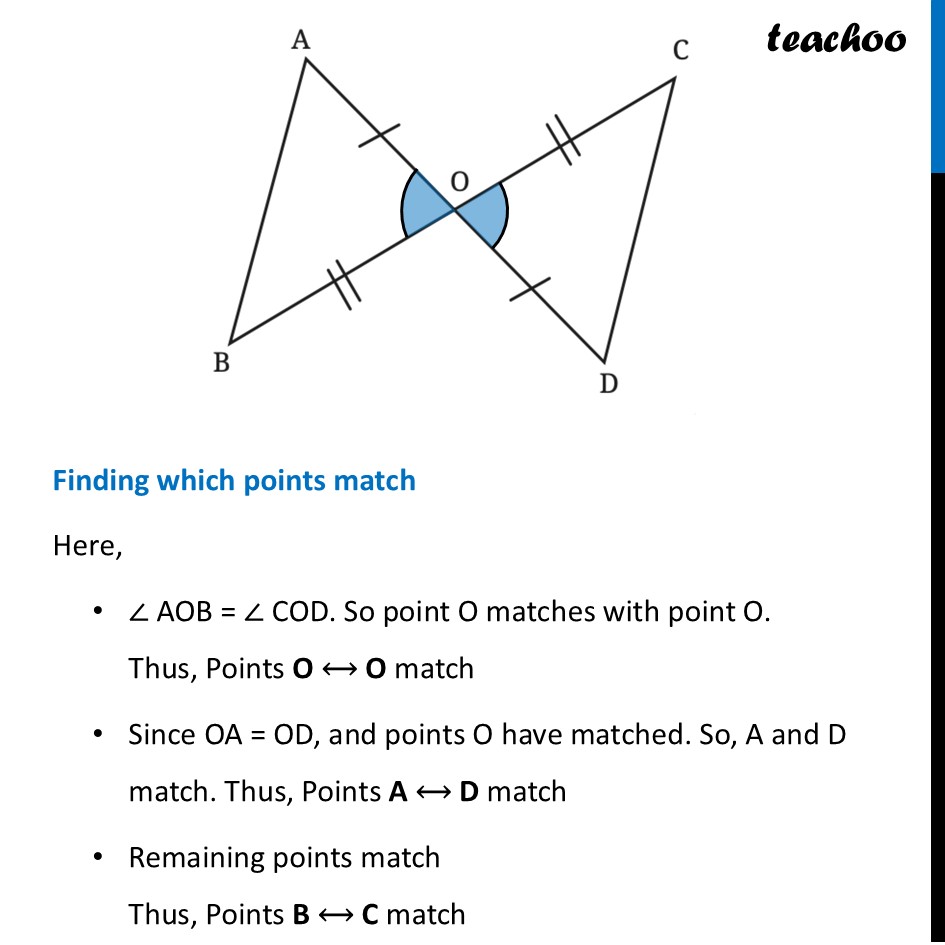
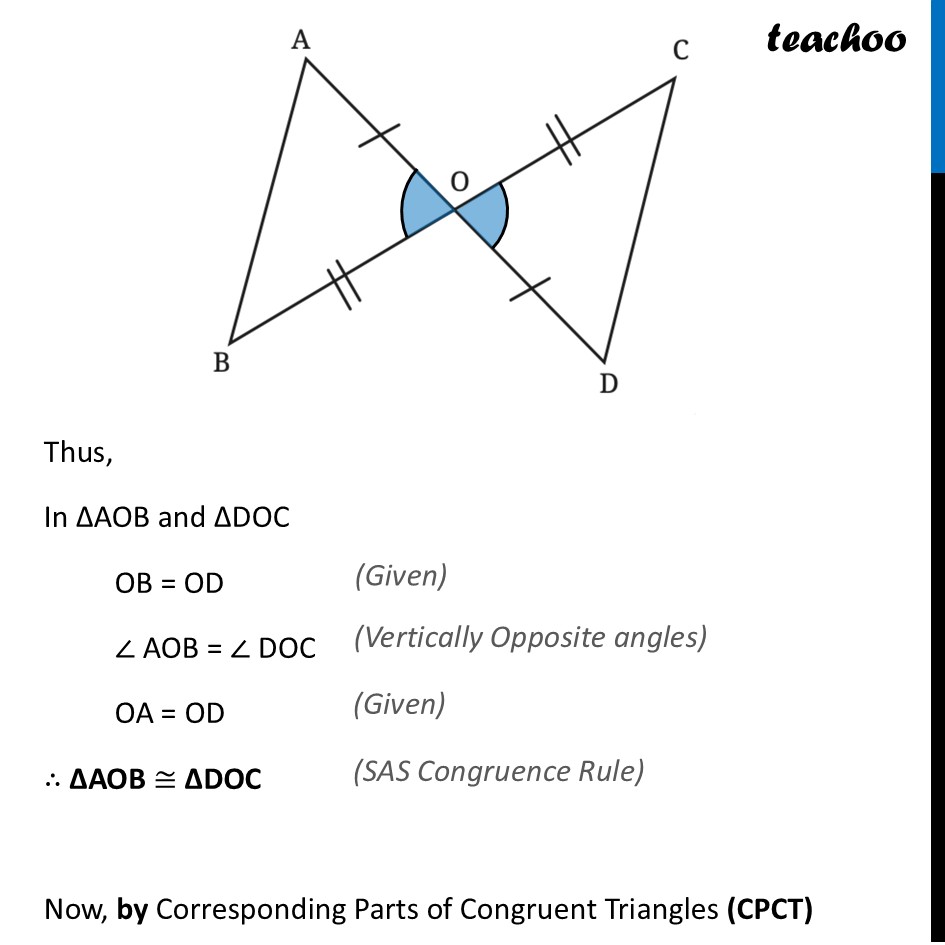
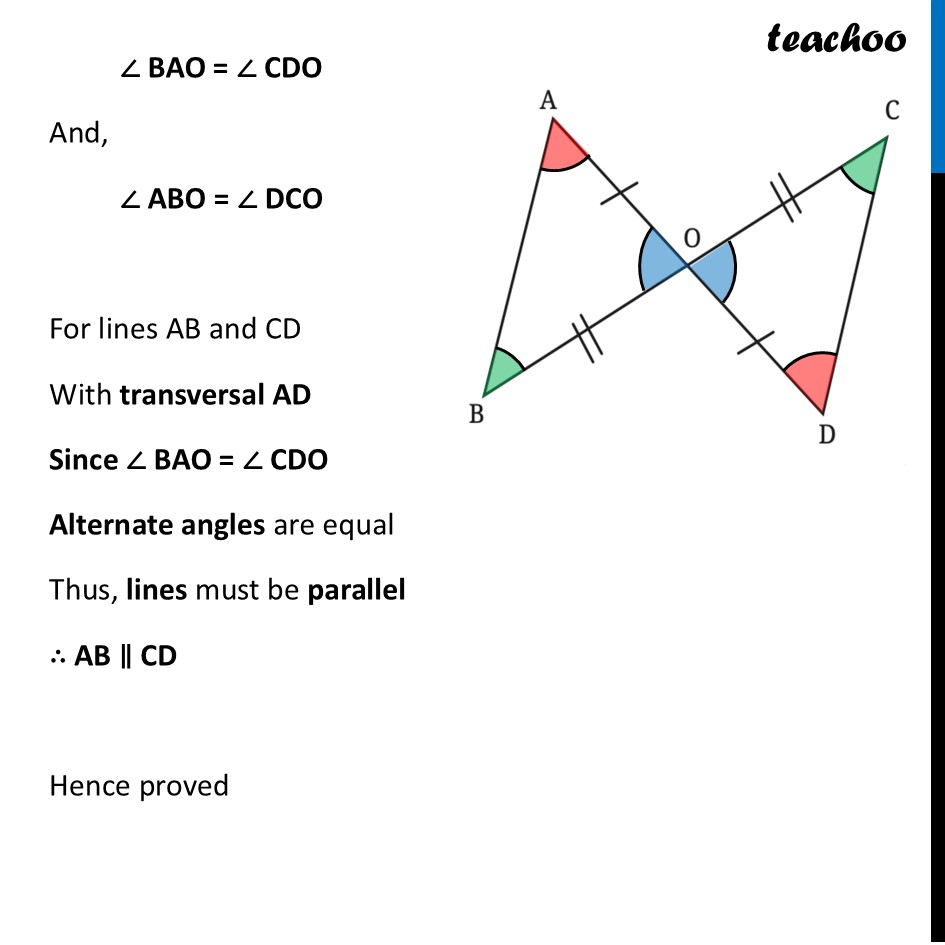
Question 3 It is given that OB = OC, and OA = OD. Show that AB is parallel to CD. [Hint: AD is a transversal for these two lines. Are there any equal alternate angles?]Since lines AD & BC intersect By Vertically Opposite Angles ∠ AOB = ∠ COD Now, let’s find which points match Finding which points match Here, ∠ AOB = ∠ COD. So point O matches with point O. Thus, Points O ⟷ O match Since OA = OD, and points O have matched. So, A and D match. Thus, Points A ⟷ D match Remaining points match Thus, Points B ⟷ C match So, we can write ∆ OAB ≅ ∆ ODC And, by Corresponding Parts of Congruent Triangles (CPCT) Corresponding sides are equal Thus, AB = DC Thus, In ∆AOB and ∆DOC OB = OD ∠ AOB = ∠ DOC OA = OD ∴ ∆AOB ≅ ∆DOC Now, by Corresponding Parts of Congruent Triangles (CPCT) (Given) ∠ BAO = ∠ CDO And, ∠ ABO = ∠ DCO For lines AB and CD With transversal AD Since ∠ BAO = ∠ CDO Alternate angles are equal Thus, lines must be parallel ∴ AB ∥ CD Hence proved