Question 1 - Page 154 - Area of Shaded Region - Chapter 6 Class 8 - We Distribute yet things Multiply (Ganita Prakash)

Transcript

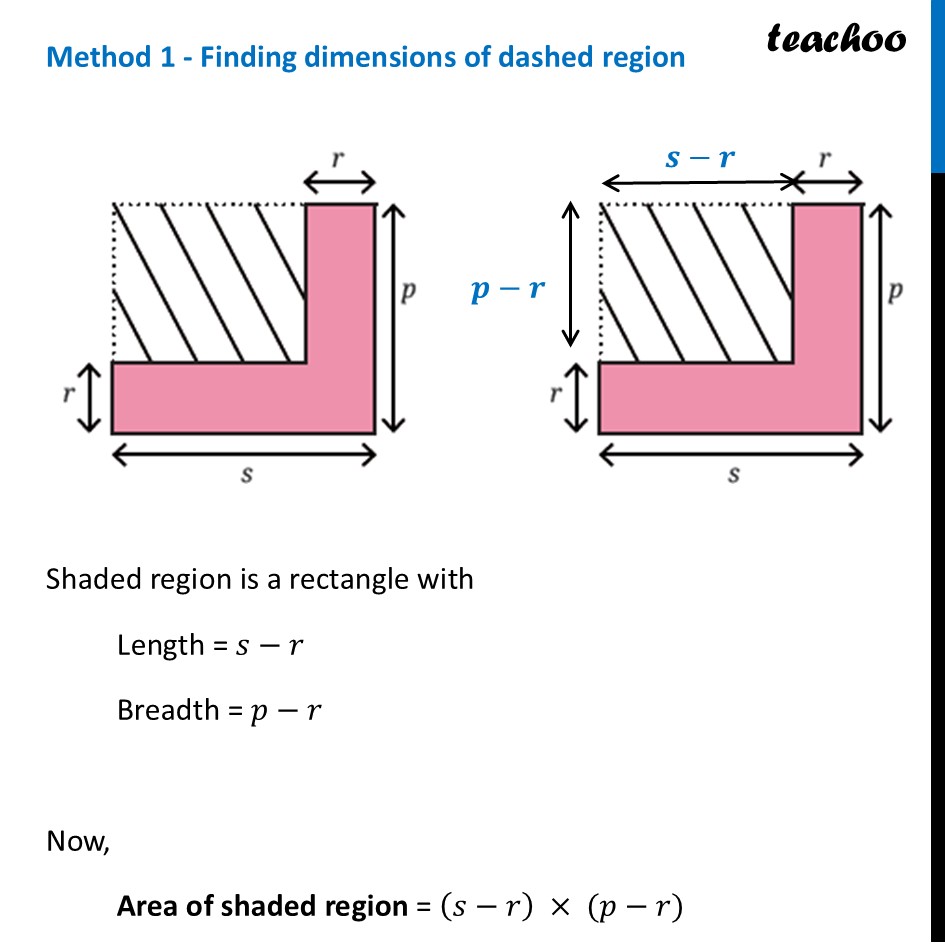
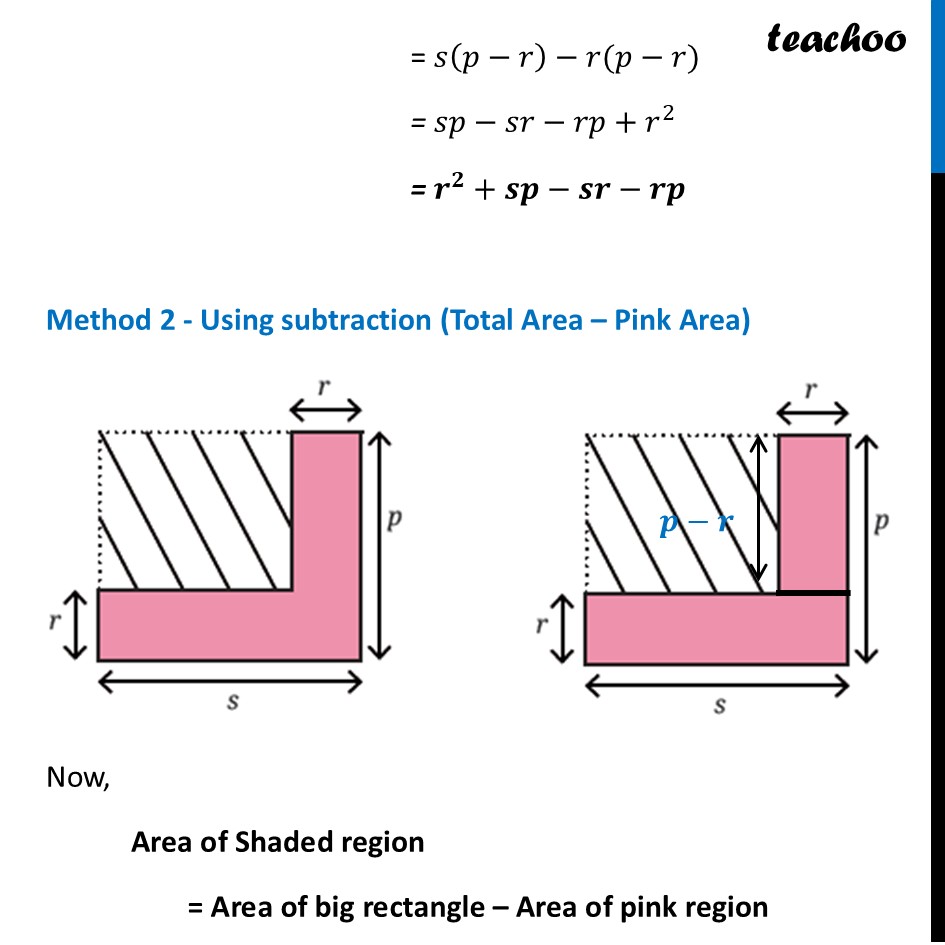
Question 1 - Page 154 Write an expression for the area of the dashed region in the figure below. Use more than one method to arrive at the answer. Substitute p = 6, r = 3.5, and s = 9, and calculate the area.Let’s use two methods for this Finding dimensions of dashed region Using subtraction (Total Area – Pink Area) Method 1 - Finding dimensions of dashed region Shaded region is a rectangle with Length = 𝑠−𝑟 Breadth = 𝑝−𝑟 Now, Area of shaded region = (𝑠−𝑟) × (𝑝−𝑟) = 𝑠(𝑝−𝑟)−𝑟(𝑝−𝑟) = 𝑠𝑝−𝑠𝑟−𝑟𝑝+𝑟^2 = 𝒓^𝟐+𝒔𝒑−𝒔𝒓−𝒓𝒑 Method 2 - Using subtraction (Total Area – Pink Area) Now, Area of Shaded region = Area of big rectangle – Area of pink region Area of big rectangle Big rectangle is a rectangle with sides p & s Area of big rectangle = 𝒑 × 𝒔 Area of pink region Pink region has two rectangles Rectangle with sides r & s Rectangle with sides (p – r) and r Thus, Area of pink region = 𝒓 × 𝒔+(𝒑−𝒓) × 𝒓 = 𝒓𝒔+𝒑𝒓 −𝒓^𝟐 Now, Area of Shaded region = Area of big rectangle – Area of pink region = 𝒑𝒔−(𝒓𝒔+𝒑𝒓−𝒓^𝟐) = 𝑝𝑠−𝑟𝑠−𝑟𝑝+𝑟^2 = 𝒓^𝟐+𝒑𝒔−𝒓𝒔−𝒓𝒑 Another part of the question was Substitute p = 6, r = 3.5, and s = 9, and calculate the area. Putting values in the equation Area of Shaded region = 𝑟^2+𝑝𝑠−𝑟𝑠−𝑟𝑝 = (𝟑.𝟓)^𝟐+𝟔 × 𝟗−𝟑.𝟓 × 𝟗−𝟑.𝟓 × 𝟔 = (7/2)^2+6 × 9−7/2 × 9−7/2 × 6 = 49/4+54−31.5−21 = 12.25+54−31.5−21 = 𝟏𝟑.𝟕𝟓 square units