Question 2 - Page 153 - Area of Shaded Region - Chapter 6 Class 8 - We Distribute yet things Multiply (Ganita Prakash)

Transcript

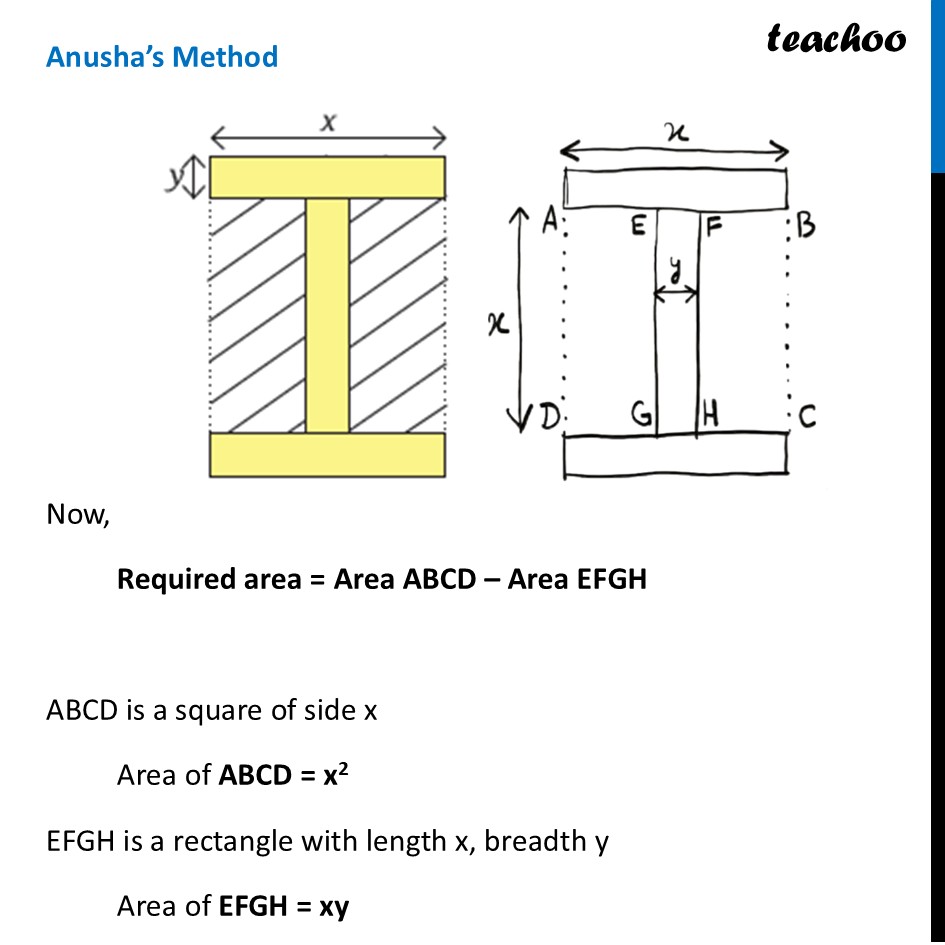
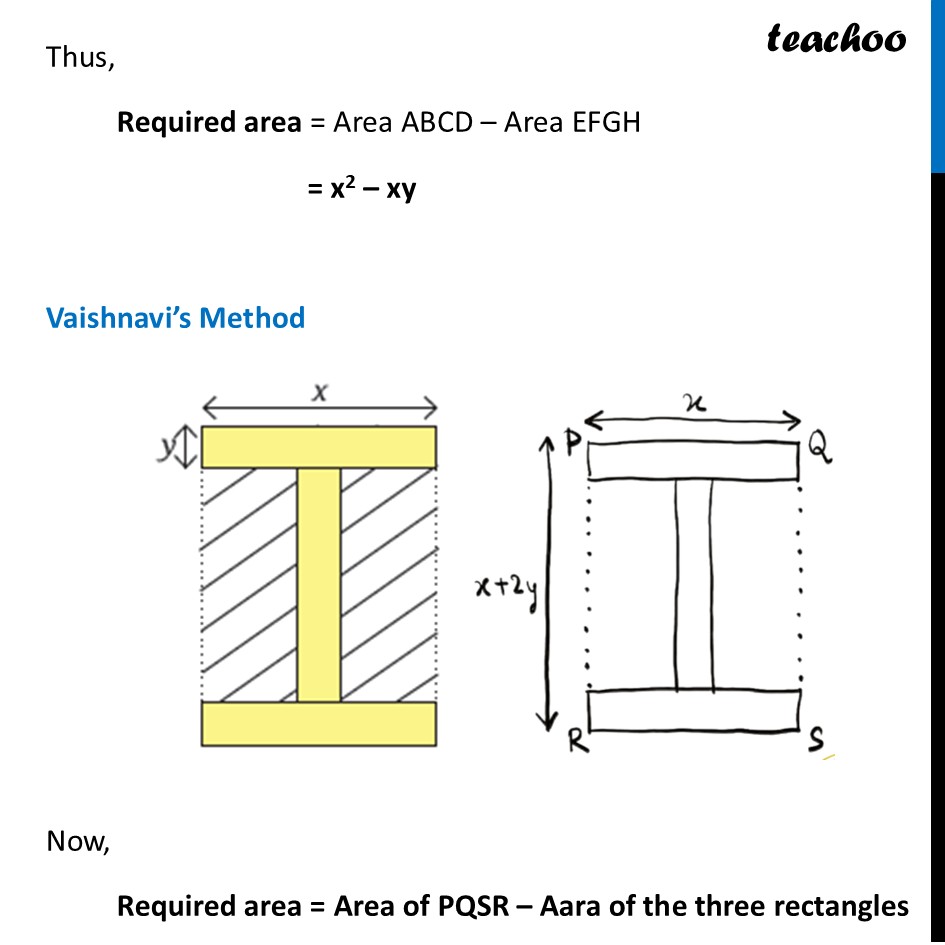
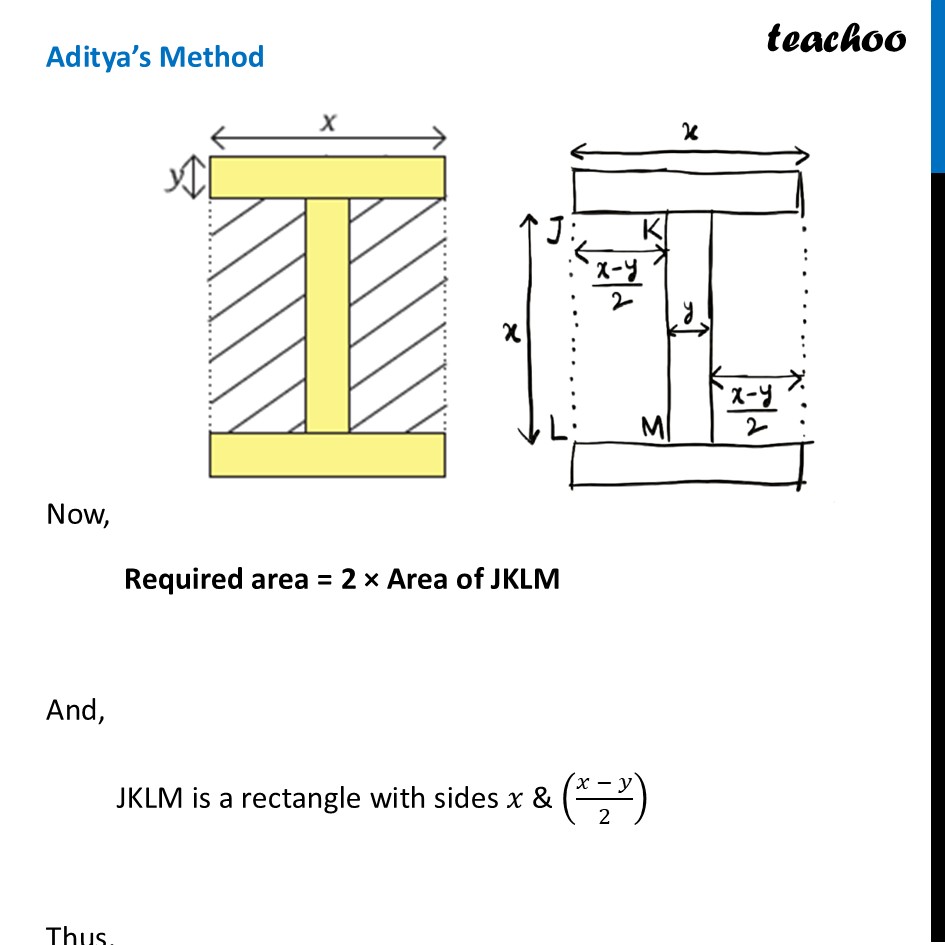
Question 2 - Page 153 Find out the area of the region with slanting lines in the figure. All three rectangles have the same dimensions. By expanding the expressions, verify that all three expressions are equivalent. If x = 8 and y = 3, find the area of the shaded region We do this by 3 methods Anusha’s Method Vaishnavi’s Method Aditya’s Method Let’s do it one by one Anusha’s Method Now, Required area = Area ABCD – Area EFGH ABCD is a square of side x Area of ABCD = x2 EFGH is a rectangle with length x, breadth y Area of EFGH = xy Thus, Required area = Area ABCD – Area EFGH = x2 – xy Thus, Required area = Area ABCD – Area EFGH = x2 – xy Vaishnavi’s Method Now, Required area = Area of PQSR – Aara of the three rectangles PQSR is a rectangle with sides x and (x + 2y) Area of PQSR = x(x + 2y) And, Three rectangels have sides x and y Area of 3 rectangles = 3 × Area of 1 rectangle = 3 × (xy) = 3xy Thus Required area = Area of PQSR – Aara of the three rectangles = x(x + 2y) – 3xy = x2 + 2xy – 3xy = x2 – xy Aditya’s Method Now, Required area = 2 × Area of JKLM And, JKLM is a rectangle with sides 𝑥 & ((𝑥 − 𝑦)/2) Thus, Area of JKLM = 𝑥 × ((𝑥 − 𝑦)/2) Now, Required area = 2 × Area of JKLM = 2 × 𝑥 × ((𝑥 − 𝑦)/2) = 𝑥 (𝑥−𝑦) =𝒙^𝟐−𝒙𝒚 Thus, Area of JKLM = 𝑥 × ((𝑥 − 𝑦)/2) Now, Required area = 2 × Area of JKLM = 2 × 𝑥 × ((𝑥 − 𝑦)/2) = 𝑥 (𝑥−𝑦) =𝒙^𝟐−𝒙𝒚 Now, the next part of our question was By expanding the expressions, verify that all three expressions are equivalent. If x = 8 and y = 3, find the area of the shaded region. We note that all 3 expressions are same Now, putting x = 8 and y = 3 in our equation Required Area = 𝑥^2−𝑥𝑦 = 𝟖^𝟐−𝟖 × 𝟑 =64−24 = 40 square units