Pattern made of Square Tiles

Transcript

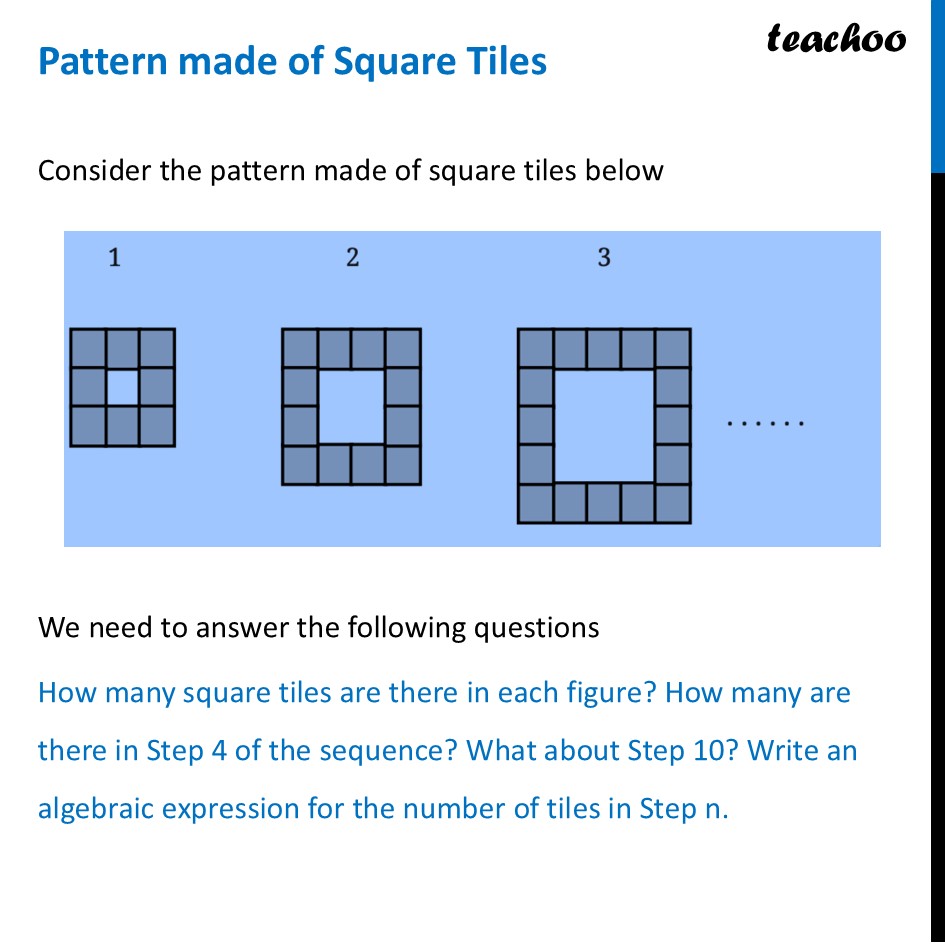
Pattern made of Square TilesConsider the pattern made of square tiles below We need to answer the following questions How many square tiles are there in each figure? How many are there in Step 4 of the sequence? What about Step 10? Write an algebraic expression for the number of tiles in Step n. We notice that we have to two squares here Outer square with tiles Inner Hole Let's count square tiles one by one using the whole method Step 1: There is a 3 × 3 square on the outside and a 1 × 1 hole in the middle. Count: 3 × 3 – 1 × 1 = 9 – 1 = 8 tiles Step 2: There is a 4 × 4 square on the outside and a 2 × 2 hole in the middle. Count: 4 × 4 – 2 × 2 = 16 – 4 = 12 tiles Step 3: There is a 5 × 5 square on the outside and a 3 × 3 hole in the middle. Count: 5 × 5 – 3 × 3 = 25 – 9 = 16 tiles The Pattern: The pattern is 8, 12, 16... The number of tiles increases by 4 every time Number of Tiles in Step 4 So, in Step 4, we will have 16 + 4 = 20 tiles Now, let’s see pattern again with Step Number (n) Finding Number of Tiles using Step Number Our pattern was 8, 12, 16, 20,…. For Step 1: It was 3 × 3 – 1 × 1 So, we can say Number of Tiles = (Number of Step + 2)2 – (Number of Step)2 = (n + 2)2 – n2 For Step 2: Putting n = 2 in formula Number of Tiles = (n + 2)2 – n2 = (2 + 2)2 – 22 = 42 – 22 = 16 – 4 = 12 So, this matches. Algebraic Expression Thus, our Algebraic Expression for Number of Tiles are Number of Tiles = (n + 2)2 – n2 = n2 + 2 × 2 × n + 22 – n2 = n2 + 4n + 4 – n2 = 4n + 4 We also need to find Number of Tiles in Step 10 Number of Tiles in Step 10 Putting n = 10 in our formula Number of tiles = (n + 2)2 – n2 = (10 + 2)2 – 102 = 122 – 102 = 144 – 100 = 44