Properties of Kite (Proof)

Transcript

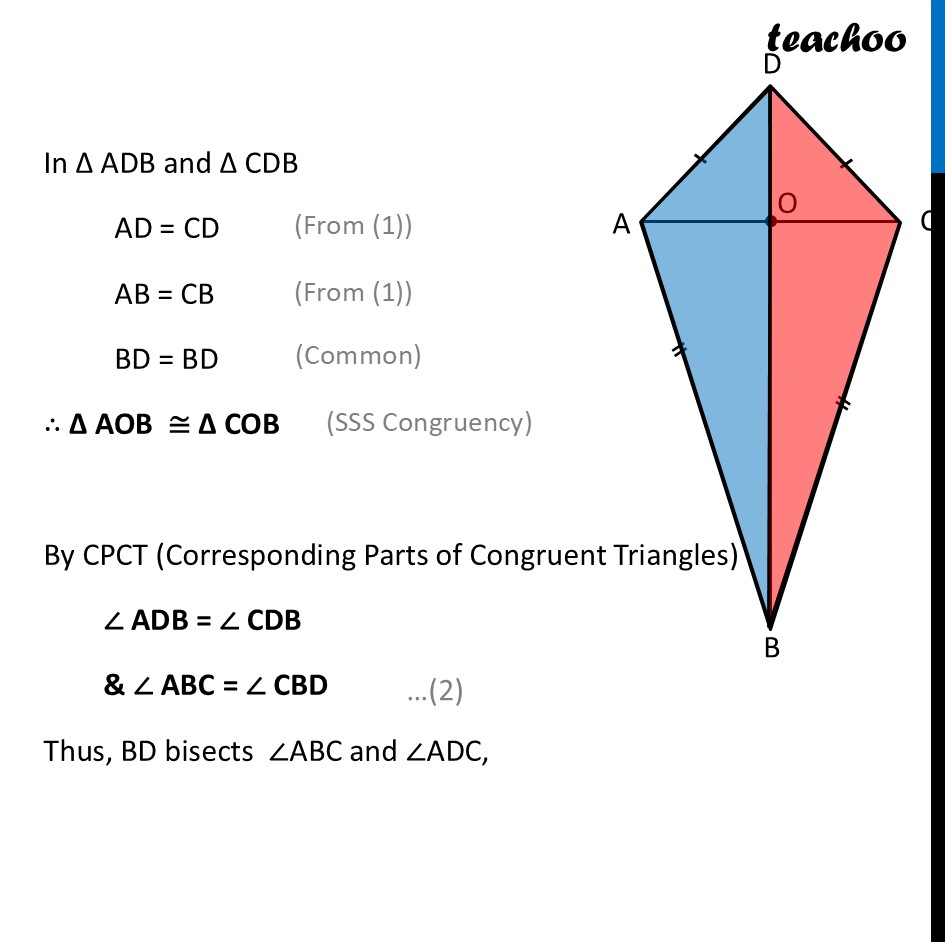
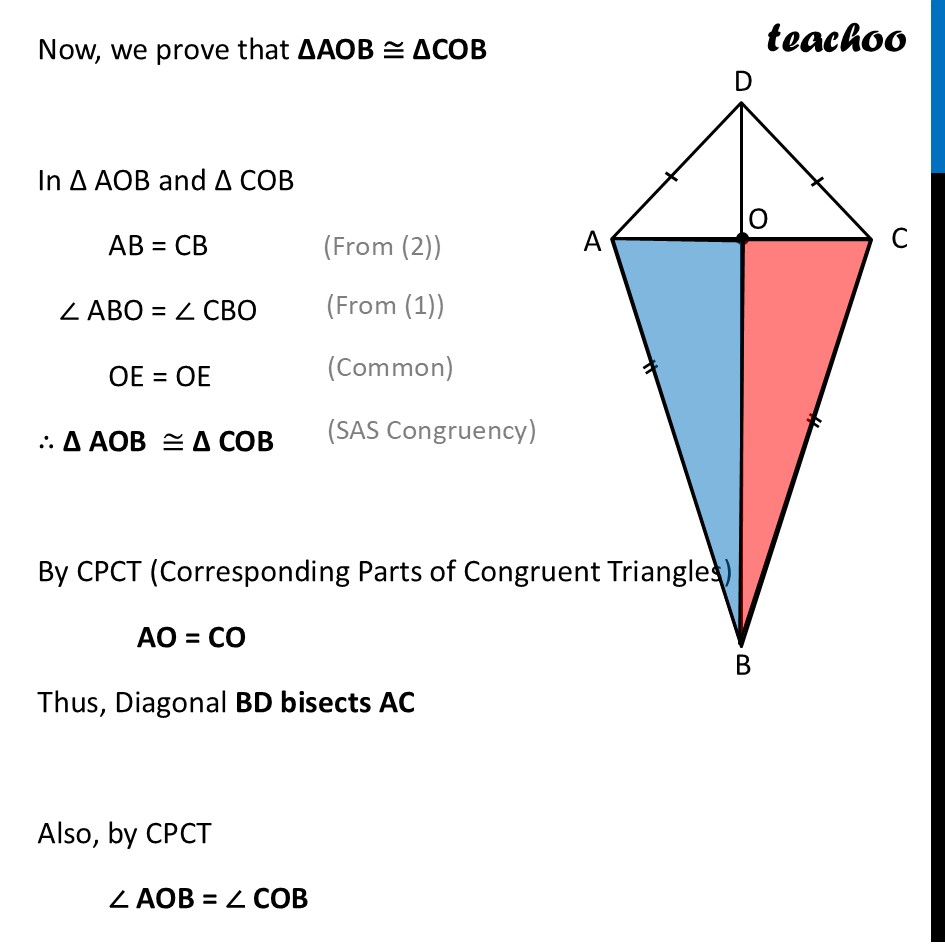
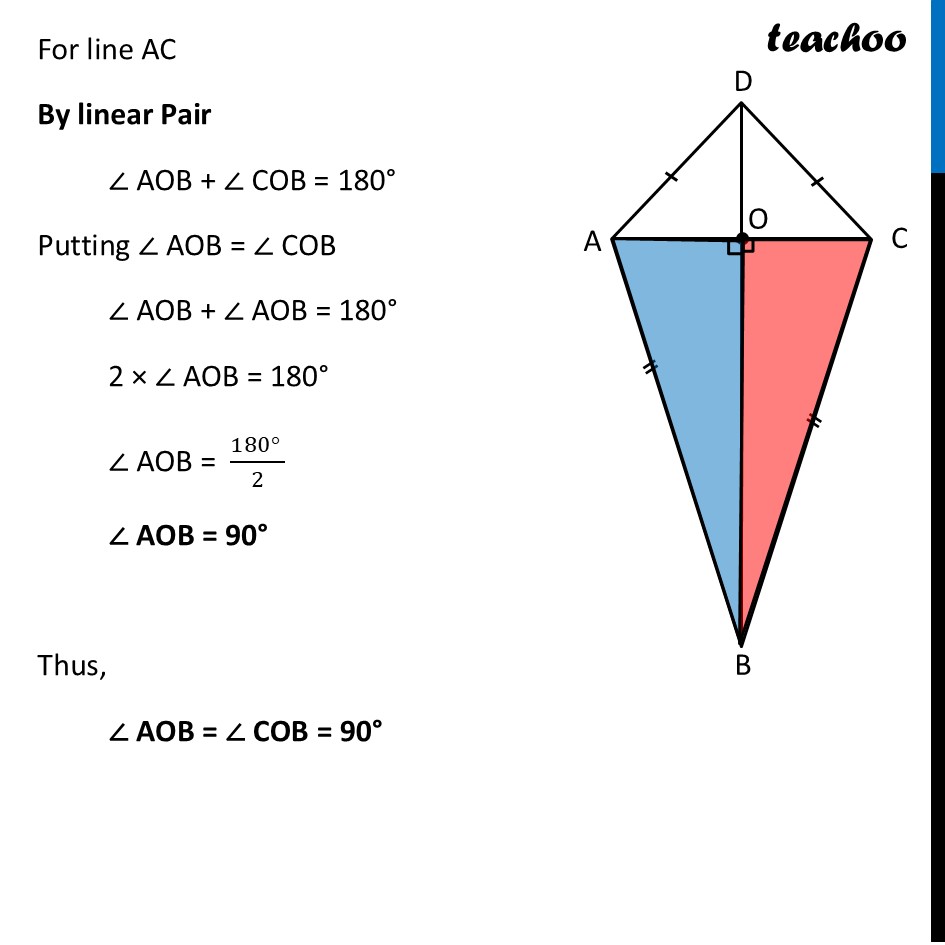
Properties of Kite (Proof)In the kite, show that the diagonal BD (i) bisects ∠ABC and ∠ADC, (ii) bisects the diagonal AC, that is, AO = OC, and is perpendicular to it. To prove this, We prove that ∆AOB ≅ ∆COB But, we cannot do that unless we prove ∆ADB ≅ ∆CDB Now, Since Kite has adjacent sides equal AB = AC & AD = CD In ∆ ADB and ∆ CDB AD = CD AB = CB BD = BD ∴ ∆ AOB ≅ ∆ COB By CPCT (Corresponding Parts of Congruent Triangles) ∠ ADB = ∠ CDB & ∠ ABC = ∠ CBD Thus, BD bisects ∠ABC and ∠ADC, Now, we prove that ∆AOB ≅ ∆COB In ∆ AOB and ∆ COB AB = CB ∠ ABO = ∠ CBO OE = OE ∴ ∆ AOB ≅ ∆ COB By CPCT (Corresponding Parts of Congruent Triangles) AO = CO Thus, Diagonal BD bisects AC Also, by CPCT ∠ AOB = ∠ COB For line AC By linear Pair ∠ AOB + ∠ COB = 180° Putting ∠ AOB = ∠ COB ∠ AOB + ∠ AOB = 180° 2 × ∠ AOB = 180° ∠ AOB = (180° )/2 ∠ AOB = 90° Thus, ∠ AOB = ∠ COB = 90°