Deduction 10 - What can we say about angles formed by diagonals of Rhombus at point of intersection

Transcript

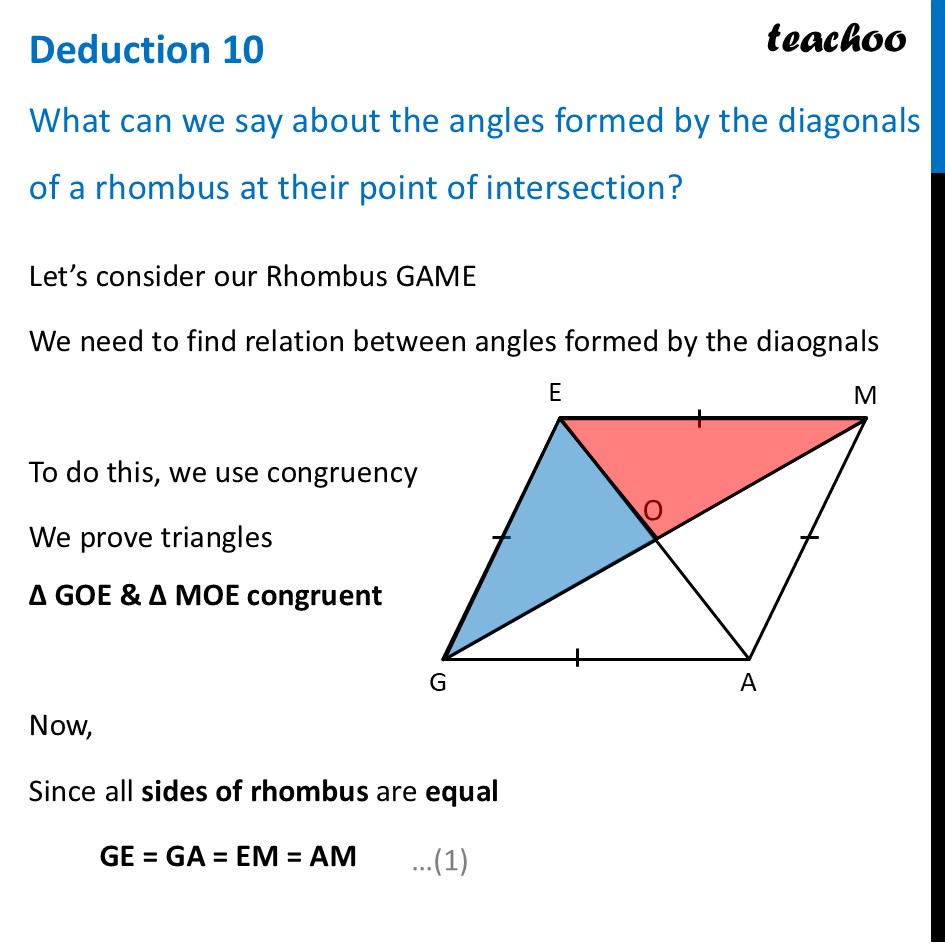
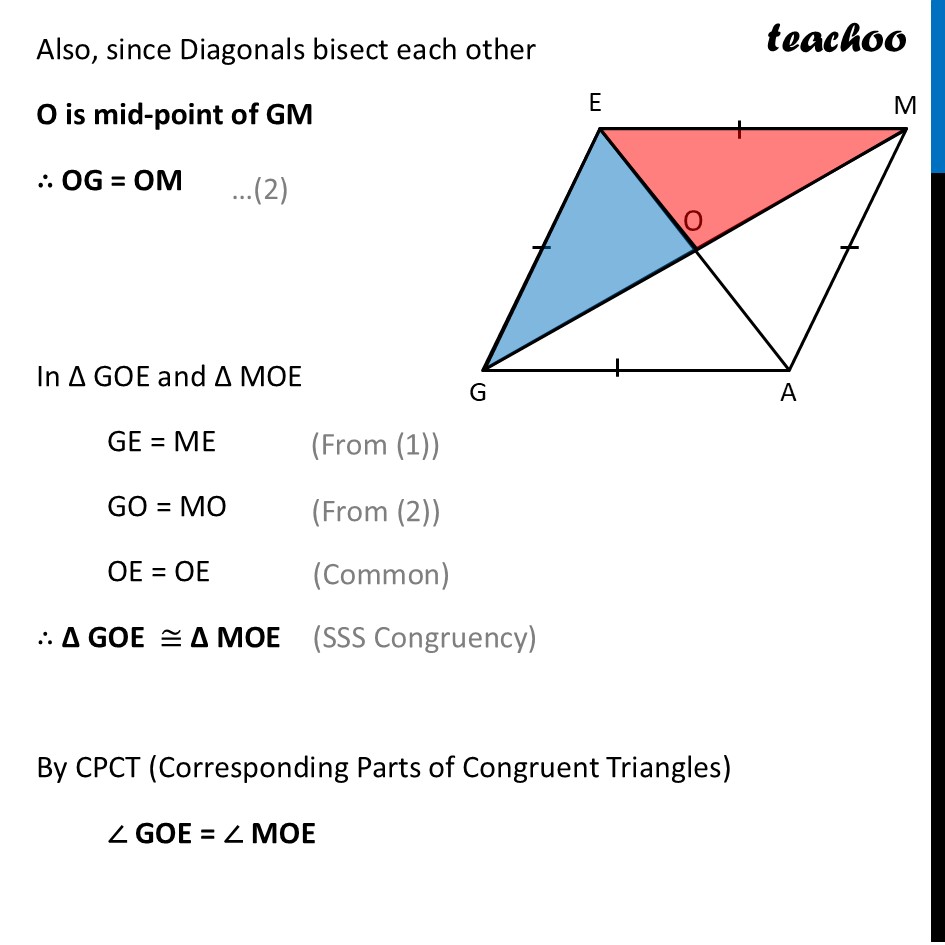
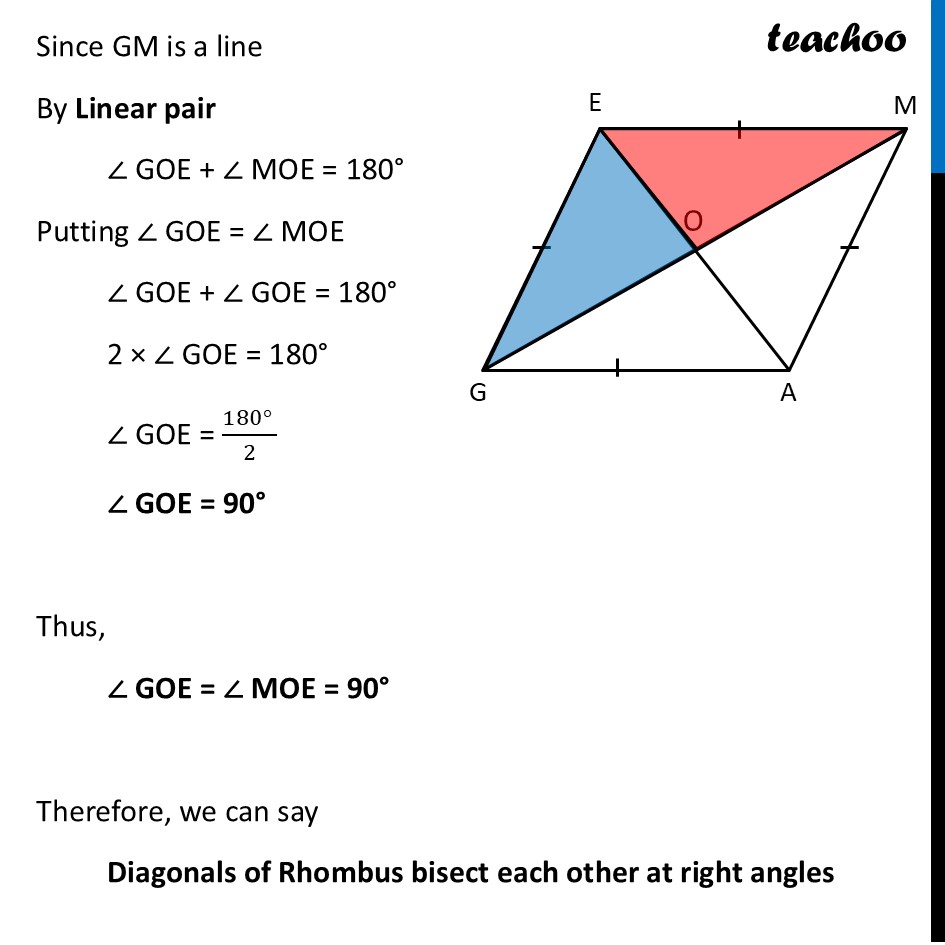
Deduction 10 What can we say about the angles formed by the diagonals of a rhombus at their point of intersection?Let’s consider our Rhombus GAME We need to find relation between angles formed by the diaognals To do this, we use congruency We prove triangles ∆ GOE & ∆ MOE congruent Now, Since all sides of rhombus are equal GE = GA = EM = AM Also, since Diagonals bisect each other O is mid-point of GM ∴ OG = OM In ∆ GOE and ∆ MOE GE = ME GO = MO OE = OE ∴ ∆ GOE ≅ ∆ MOE By CPCT (Corresponding Parts of Congruent Triangles) ∠ GOE = ∠ MOE Since GM is a line By Linear pair ∠ GOE + ∠ MOE = 180° Putting ∠ GOE = ∠ MOE ∠ GOE + ∠ GOE = 180° 2 × ∠ GOE = 180° ∠ GOE = (180° )/2 ∠ GOE = 90° Thus, ∠ GOE = ∠ MOE = 90° Therefore, we can say Diagonals of Rhombus bisect each other at right angles