Diagonal bisecting angle of Square

Transcript

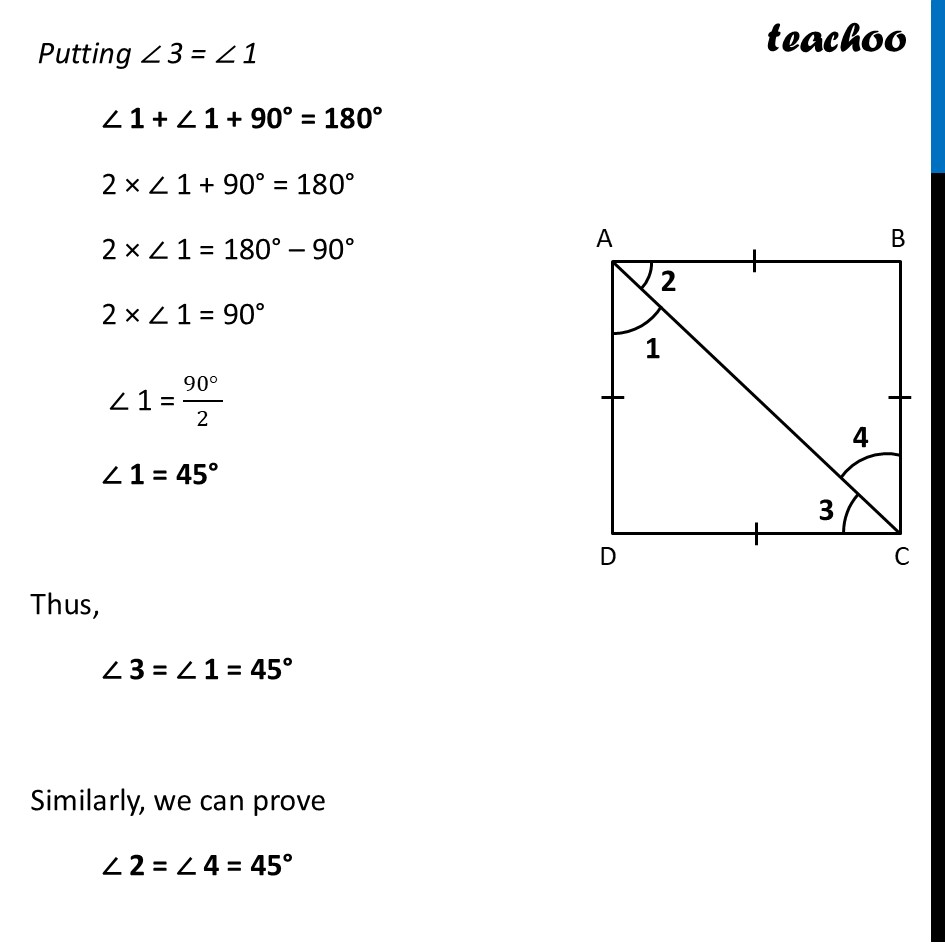
Diagonal bisecting angle of SquareWe have to find angles ∠ 1, ∠ 2, ∠ 3, ∠ 4 In ∆ ADC Since AD = CD By Isosceles Triangle property Angles opposite equal side is equal ∴ ∠ 1 = ∠ 3 Also, in ∆ ACD By Angle sum property of triangle ∠ 1 + ∠ 3 + ∠ D = 180° ∠ 1 + ∠ 3 + 90° = 180° Putting ∠ 3 = ∠ 1 ∠ 1 + ∠ 1 + 90° = 180° 2 × ∠ 1 + 90° = 180° 2 × ∠ 1 = 180° – 90° 2 × ∠ 1 = 90° ∠ 1 = (90° )/2 ∠ 1 = 45° Thus, ∠ 3 = ∠ 1 = 45° Similarly, we can prove ∠ 2 = ∠ 4 = 45° Thus, we write ∠ 1 = ∠ 2 = ∠ 3 = ∠ 4 = 45° So, we can say that The diagonals of a square divide the angles of the square into equal halves Or we can write The diagonals of a square bisect the angles of the square