Deduction 5 - What should be the angle formed by the diagonals?

Transcript

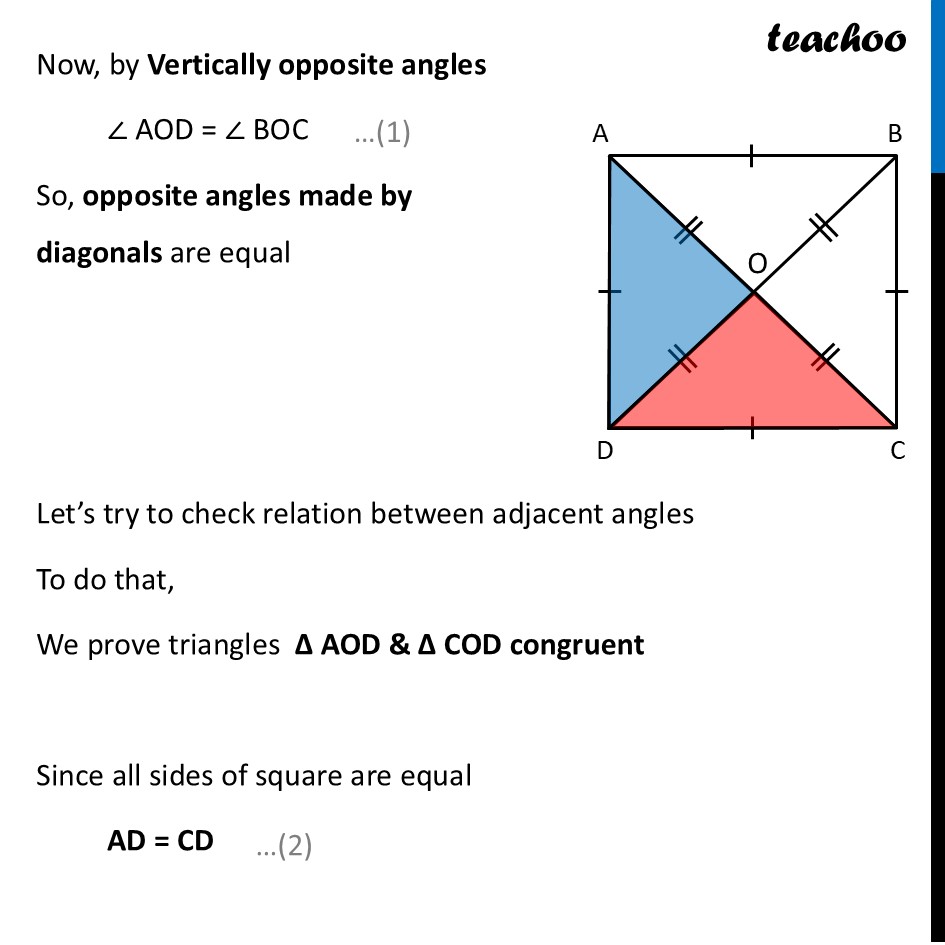
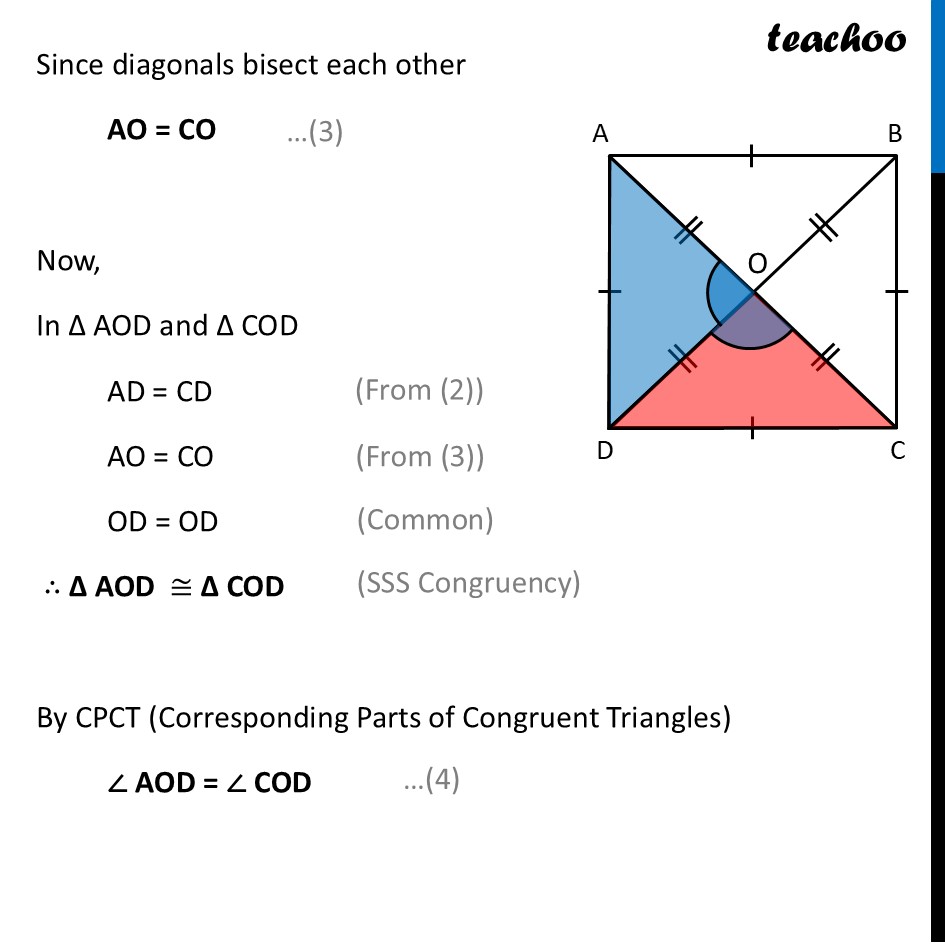
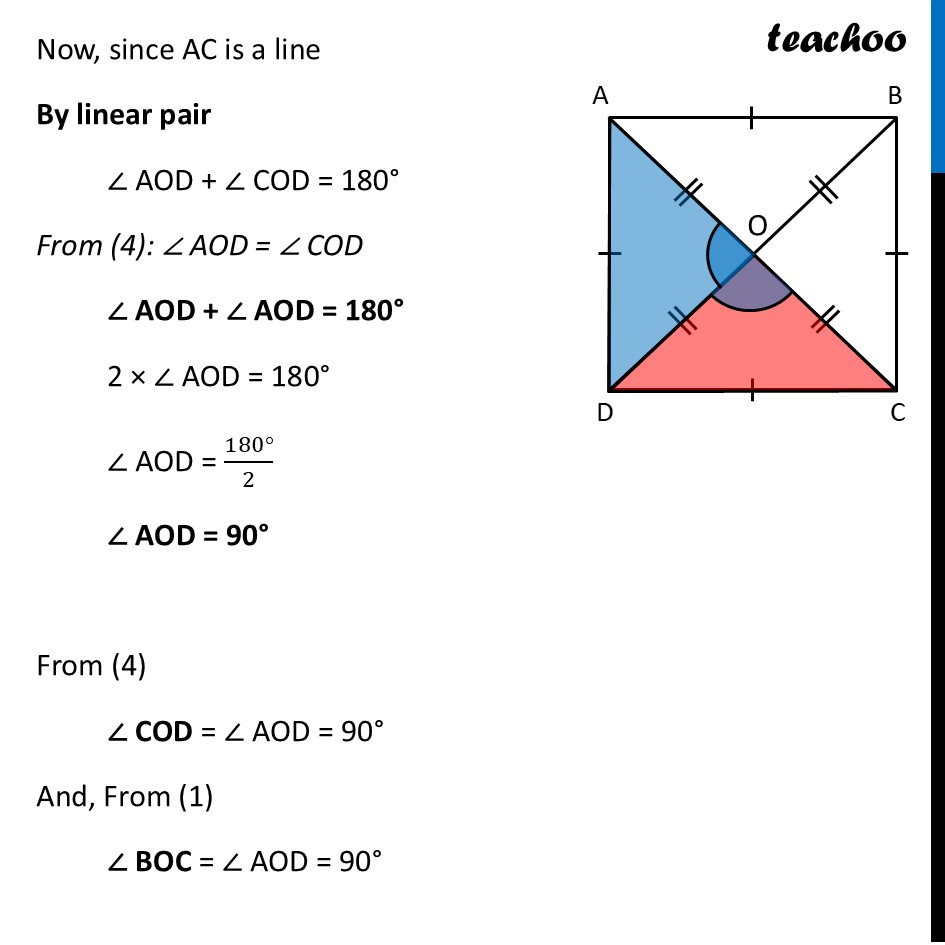
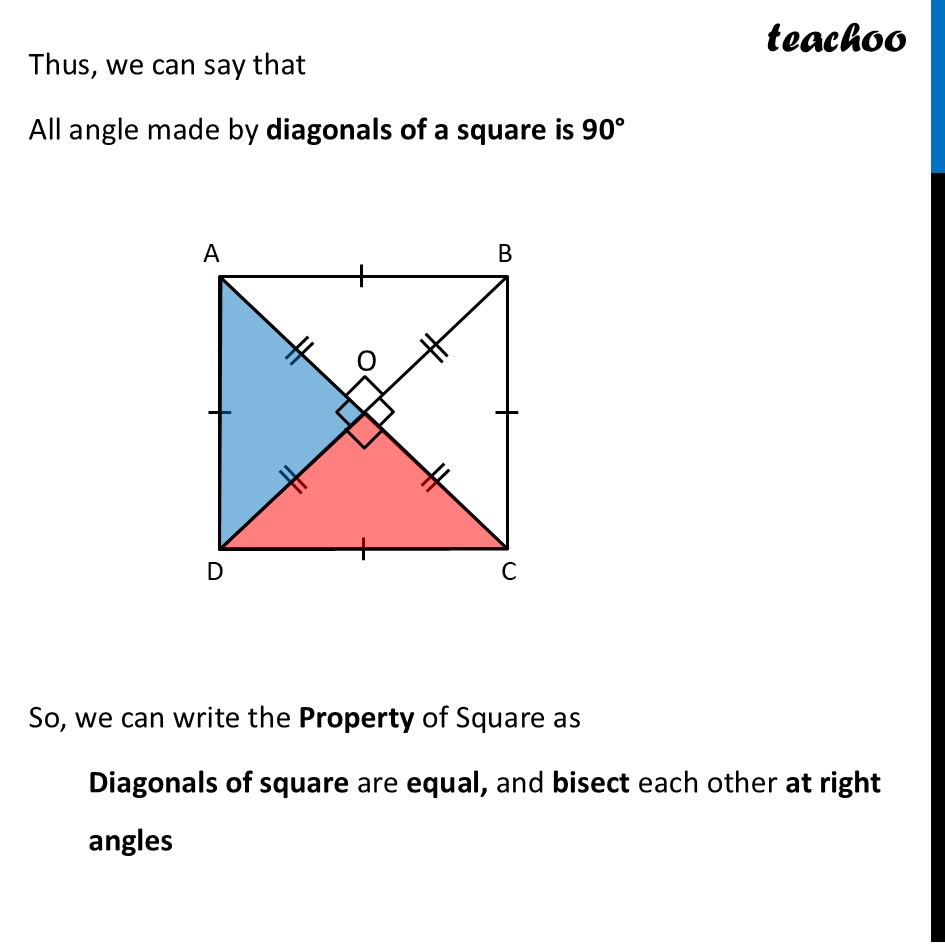
Deduction 5 What should be the angle formed by the diagonals of a square?Since all squares are rectangles Squares will have all rectangle properties Thus, Diagonals of a square are equal Diagonals of a square bisect each other Now, we just need to check angles between two diagonals of a square Now, by Vertically opposite angles ∠ AOD = ∠ BOC So, opposite angles made by diagonals are equal Let’s try to check relation between adjacent angles To do that, We prove triangles ∆ AOD & ∆ COD congruent Since all sides of square are equal AD = CD Since diagonals bisect each other AO = CO Now, In ∆ AOD and ∆ COD AD = CD AO = CO OD = OD ∴ ∆ AOD ≅ ∆ COD By CPCT (Corresponding Parts of Congruent Triangles) ∠ AOD = ∠ COD Now, since AC is a line By linear pair ∠ AOD + ∠ COD = 180° From (4): ∠ AOD = ∠ COD ∠ AOD + ∠ AOD = 180° 2 × ∠ AOD = 180° ∠ AOD = (180°)/2 ∠ AOD = 90° From (4) ∠ COD = ∠ AOD = 90° And, From (1) ∠ BOC = ∠ AOD = 90° Thus, we can say that All angle made by diagonals of a square is 90° So, we can write the Property of Square as Diagonals of square are equal, and bisect each other at right angles